Wenn sich eine zweidimensionale Figur (zum Beispiel ein Dreieck, Rechteck, Halbkreis,… ) sehr schnell um eine Achse dreht, entsteht ein räumlicher Körper.
Einen solchen Körper nennt man Rotationskörper.
Beispiel, wie aus einer rotierenden Fläche ein Rotationskörper wird
Eigenschaften eines Rotationskörpers
Wenn eine Figur sich um eine Achse dreht, nennt man den daraus entstehenden Körper, einen Rotationskörper. Die Achse, um welche sich die Figur dreht, nennt man Rotationsachse.
Ein Rotationskörper besteht aus all denjenigen Punkten, die im Verlauf der Drehung von der rotierenden Fläche erfasst werden.
Ein Rotationskörper ist stets zu seiner Rotationsachse symmetrisch.
Axialschnitt eines Rotationskörpers
Schneidet man einen Rotationskörper längs seiner Achse durch, erhält man den Axialschnitt des Körpers.
Wenn du lernen willst, wie man einen Rotationskörper auf das Papier zeichnet, gehe zum Artikel Skizzieren eines Rotationskörpers - Anleitung.
Volumen und Oberfläche eines Rotationskörpers berechnen
Einfache Rotationskörper
Diese sind Körper, die aus der Drehung von Flächen wie Rechtecke, Dreiecke und Kreise entstehen. Wenn man mehrere solche einfache Rotationskörper zusammenstellt, kann man komplexere Figuren darstellen.
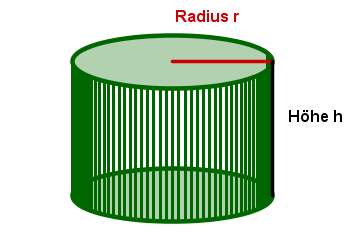
Zylinder
Einen Zylinder (oder genauer: einen geraden Kreiszylinder) kann man sich dadurch entstanden denken, dass ein Rechteck um eine seiner Seiten rotiert.
Wichtige Formeln für den Zylinder:
Volumen: | |
|---|---|
Oberfläche: | |
Mantelfläche: |

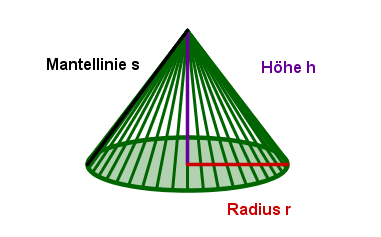
Kegel
Einen Kegel (oder genauer: einen geraden Kreiskegel) kann man sich dadurch entstanden denken, dass ein rechtwinkliges Dreieck um eine seiner Katheten rotiert.
Wichtige Formeln für den Kegel:
Volumen: | |
|---|---|
Oberfläche: | |
Mantelfläche: |
Kugel
Eine Kugel kann man sich dadurch entstanden denken, dass ein Kreis rotiert.
Wichtige Formeln für die Kugel:
Volumen: | |
|---|---|
Oberfläche: | |
Mantelfläche: | s. Oberfläche |

Zusammengesetzte Rotationskörper
Wenn man einfache Flächen, wie einen Kreis, ein Dreieck oder ein Rechteck kombiniert und anschließend dreht, entstehen zusammengesetzte Rotationskörper.
Deren Volumen lässt sich auf folgende Weisen berechnen:
Indem man sie in einfache Körper aufteilt und deren Volumen getrennt berechnet, oder
mittels Integration.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Rotationskörpern
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
