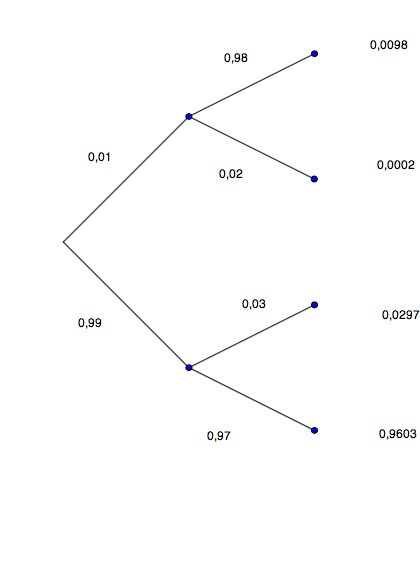
In einem Land der Dritten Welt leiden 1% der Menschen an einer bestimmten Infektionskrankheit. Ein Test zeigt die Krankheit bei den tatsächlich Erkrankten zu 98% korrekt an. Leider zeigt der Test auch 3% der Gesunden als erkrankt an.
Stellen Sie den Sachzusammenhang in einer 4-Feldtafel da. Verwenden Sie die Ereignisse (mit ihren Gegenereignissen):
K: Die getestete Person ist krank.
T: Testergebnis ist positiv (Person wurde als krank getestet).
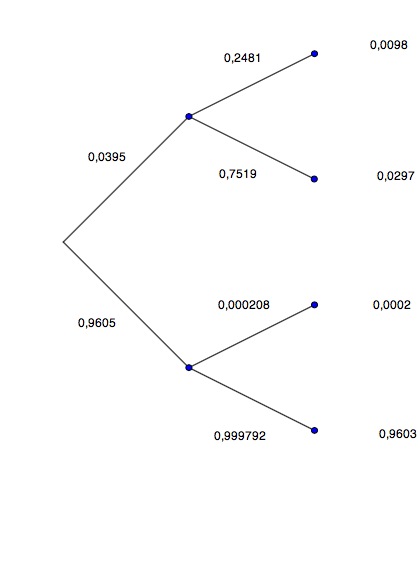
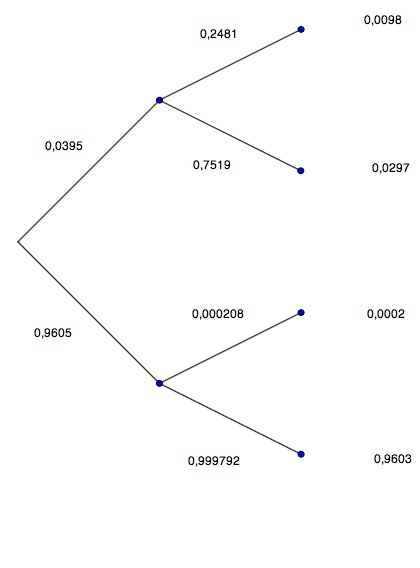
Zeichnen Sie das Baumdiagramm und den inversen Baum. Bestimmen Sie alle Pfadwahrscheinlichkeiten.
Mit welcher Wahrscheinlichkeit zeigt der Test bei einer zufällig ausgewählten Person ein positives Ergebnis?
Mit welcher Wahrscheinlichkeit ist eine positiv getestete Person auch tatsächlich krank? Kommentieren Sie das Ergebnis.
Mit welcher Wahrscheinlichkeit ist eine als negativ getestete Person gesund? Kommentieren Sie das Ergebnis.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?