Aufgaben zum Thema bedingte Wahrscheinlichkeit

Wie gut kennst du dich aus? Lerne mit diesen gemischten Aufgaben, bedingte Wahrscheinlichkeiten zu berechnen!

1
Herr Huber hat eine Alarmanlage in seinem Auto installiert. Es werden die Ereignisse A: „Alarmanlage springt an“ und K: „Jemand versucht, das Auto aufzubrechen“ betrachtet. Beschreiben Sie folgende bedingte Wahrscheinlichkeiten mit Worten: $P_K\left(\overline{A}\right),\;P_{\overline K}\left(A\right),\;P_K\left(A\right),\;P_A\left(K\right)$ .
Welche dieser bedingten Wahrscheinlichkeiten sollten hoch bzw. niedrig sein?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stochastik
$P_K\left(\overline A\right)$ : Die Wahrscheinlichkeit, dass die Alarmanlage nicht anspringt unter der Bedingung, jemand versucht das Auto aufzubrechen.
Die Wahrscheinlichkeit sollte niedrig sein.
$P_{\overline K}\left(A\right)$ : Die Wahrscheinlichkeit, dass die Alarmanlage anspringt unter der Bedingung, niemand versucht das Auto aufzubrechen.
Die Wahrscheinlichkeit sollte ebenfalls niedrig sein.
$P_K\left(A\right)$ : Die Wahrscheinlichkeit, dass die Alarmanlage anspringt unter der Bedingung, jemand versucht das Auto aufzubrechen.
Die Wahrscheinlichkeit sollte hoch sein.
$P_A\left(K\right)$ : Die Wahrscheinlichkeit, dass jemand versucht das Auto aufzubrechen unter der Bedingung, die Alarmanlage springt an.
Dies wäre nicht sehr klug.
2
Bestimme die Wahrscheinlichkeit, beim zweimaligen Werfen eines Würfels eine Augensumme von mindestens 8 zu erhalten, unter der Bedingung, dass beim ersten Wurf eine 4 gefallen ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
Ereignisse definieren
$A$ : Augensumme ist mindestens 8
$B$ : Beim ersten Wurf fällt eine 4
Dabei ist $A$ das gesuchte Ereignis ohne die Bedingung und in $B$ wurde die Bedingung als eigenes Ereignis formuliert.
Definition der bedingten Wahrscheinlichkeit angeben
Gib nun die Definition der bedingten Wahrscheinlichkeit an, die hier gesucht ist:
$\displaystyle P_B(A)=\frac{P(A\cap B)}{P(B)}$
Benötigte Wahrscheinlichkeiten herausfinden
Ermittle noch die benötigten Wahrscheinlichkeiten.
$P(B)=?$
Die Wahrscheinlichkeit, bei einem Wurf eine 4 zu bekommen, ist $\dfrac16$ .
$P(B)=\dfrac16$
$P(A\cap B)=?$
Überlege dir zuerst, welche Zahlenkombinationen in der Menge $A\cap B$ sind.
Das sind alle Zahlenpaare, die zuerst eine 4 haben und mit der zweiten Zahl zusammen mindestens 8 ergeben. Also (4,4), (4,5), (4,6). Das heißt, es gibt 3 Möglichkeiten in $A\cap B$ .
Insgesamt gibt es 36 Möglichkeiten, wenn man zweimal würfelt; daher steht im Nenner eine 36.
$P(A\cap B)=\dfrac3{36}$
Setze die Werte in die Definition ein und berechne das Ergebnis.

Die Wahrscheinlichkeit, mit zwei Würfeln einen Pasch (11, 22, . . . , 66) zu erhalten, beträgt bekanntlich $\frac16$ .

Es wird 4-mal hintereinander jeweils mit 2 Würfeln gewürfelt. Wie groß ist die Wahrscheinlichkeit, dass insgesamt genau 3-mal Pasch fällt, wenn bekannt ist, dass mindestens einmal Pasch dabei war?
Für diese Aufgabe benötigst Du folgendes Grundwissen: bedingte Wahrscheinlichkeit
Definiere Ereignisse
Definiere zunächst die Ereignisse, die in der Aufgabenstellung beschrieben werden.
Ereignis $A$ : Es fällt bei den vier Würfen genau drei mal ein Pasch.
Ereignis $B$ : Es fällt bei den vier Würfen mindestens ein Pasch.
Definiere Wahrscheinlichkeiten
Die Wahrscheinlichkeit, dass bei einem Wurf ein Pasch auftritt, ist $P(\text{Pasch bei einem Wurf}) = \frac{1}{6}.$ Die Wahrscheinlichkeit, dass bei einem Wurf kein Pasch auftritt, ist $P(\overline{\text{Pasch bei einem Wurf}}) = \frac{5}{6}.$
Definiere dann jeweils die Wahrscheinlichkeit, mit denen eins der zuvor definierten Ereignisse eintritt.
$P(A)$ : Wahrscheinlichkeit, dass bei den vier Würfen genau drei mal ein Pasch fällt.
$P(B)$ : Wahrscheinlichkeit, dass bei den vier Würfen mindestens ein Pasch fällt.
$P(A \cap B)$ : Wahrscheinlichkeit, dass bei den vier Würfen genau drei mal ein Pasch und mindestens ein Pasch fällt.
Dabei ist die Wahrscheinlichkeit $P(A \cap B)$ genau so groß wie die Wahrscheinlichkeit $P(A)$ . Wenn genau drei Päsche fallen, dann wurde natürlich mehr als ein Pasch (nämlich drei Päsche) gewürfelt.
$P_B (A)$ Wahrscheinlichkeit, dass bei den vier Würfen genau drei mal ein Pasch fällt, wenn bekannt ist, dass mindestens ein Pasch gefallen ist.
Berechne bedingte Wahrscheinlichkeit
Dazu musst du die Formel für die Berechnung von bedingten Wahrscheinlichkeiten kennen.
$P(A \cap B) = \, ?$
Berechne $P(A \cap B)$ .
Fallen genau drei Päsche, so fällt auch mindestens ein Pasch.
$P(A \cap B) = P(A)$
$P(A) = \, ?$
Berechne $P(A)$ .
3 mal Wahrscheinlichkeit für Pasch: $\frac{1}{6}$ 1 mal Wahrscheinlichkeit für kein Pasch: $\frac{5}{6}$ kombinatorischer Faktor: 4
$P(A) = 4 \cdot \left(\frac{1}{6}\right)^3 \cdot \frac{5}{6} = \frac{5}{324} = 0{,}015$
$P(B) = \, ?$
Berechne $P(B)$ .
Nutze das Gegenereignis: $P(\overline B)$ : Wahrscheinlichkeit, dass bei allen 4 Würfen kein Pasch fällt.
$P(B) = 1 - P(\overline {B})$
4 mal Wahrscheinlichkeit für kein Pasch: $\frac{5}{6}$
$P(\overline{B})=\left(\frac{5}{6}\right)^4$
$P(B) = 1 - P(\overline {B}) =1- \frac{625}{1296} =\frac{1296}{1296}- \frac{625}{1296}=\frac{671}{1296}\approx0{,}52$
Berechne bedingte Wahrscheinlichkeit
Ergebnis
Die Wahrschenlichkeit, dass genau drei Päsche fallen, wenn bekannt ist, dass mindestens ein Pasch gefallen ist, beträgt $3{,}0 \%$ .
Ergänzung
Weil es einige Nachfragen zu der Lösung gab, wird sie nochmal etwas anders berechnet.
Berechne die Wahrscheinlichkeiten für keinen, einen, zwei, drei oder vier Päsche. Beachte dabei wie oben die kombinatorischen Faktoren: bei einem oder drei Päschen gibt es je vier Möglichkeiten, an welcher Stelle der Pasch (oder der Wurf ohne Pasch) auftritt. Bei zwei Päschen sind es $\displaystyle{4\choose 2}=6$ Möglichkeiten, die du dir zur Not wie oben noch einmal aufschreiben kannst. Da wir die Zahlen vergleichen wollen, kürzen wir in der folgenden Rechnung nicht.
Kein Pasch: $\displaystyle P_0=\left(\frac{5}{6}\right)^4=\frac{625}{1296}$
Ein Pasch: $\displaystyle P_1=\left(\frac{5}{6}\right)^3\cdot\frac{1}{6}\cdot4=\frac{500}{1296}$
Zwei Päsche: $\displaystyle P_2=\left(\frac{5}{6}\right)^2\cdot\left(\frac{1}{6}\right)^2\cdot6=\frac{150}{1296}$
Drei Päsche: $\displaystyle P_3=\left(\frac{5}{6}\right)^1\cdot\left(\frac{1}{6}\right)^4\cdot4=\frac{20}{1296}$
Vier Päsche: $\displaystyle P_4=\left(\frac{1}{6}\right)^4=\frac{1}{1296}$
Wenn du zur Probe die Wahrscheinlichkeiten addierst, siehst du, dass du $P_0+P_1+P_2+P_3+P_4=1$ erhältst.
Die Wahrscheinlichkeit, genau drei Päsche zu würfeln, ist als $\displaystyle P_3=\frac{20}{1296}=\frac{5}{324}$ .
Jetzt ist aber die bedingte Wahrscheinlichkeit gefragt, drei Päsche zu würfeln, wenn schon bekannt ist, dass mindestens ein Pasch fällt. Das bedeutet, dass das Ereignis "kein Pasch" nicht mehr in der Grundmenge vorkommt. Daher ist diese bedingte Wahrscheinlichkeit
$\displaystyle P_B(A)=\frac{P_3}{P_1+P_2+P_3+P_4}=\frac{P_3}{1-P_0}=\frac{\frac{20}{1296}}{\frac{671}{1296}}=\frac{20}{671}\approx 3{,}0\%$ .
Das ist genau das, was oben berechnet worden ist.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Angenommen, Pasch fällt bei vier Würfen insgesamt genau 3-mal.
Mit welcher Wahrscheinlichkeit waren dann diese drei Pasch-Würfe hintereinander?
Für diese Aufgabe benötigst Du folgendes Grundwissen: bedingte Wahrscheinlichkeit
Definiere Ereignisse
Definiere zunächst die Ereignisse, die in der Aufgabenstellung beschrieben werden.
Ereignis $A$ : Es fällt bei den vier Würfen genau drei mal ein Pasch.
Ereignis $C$ : Die drei Pasch-Würfe fallen hintereinander.
Definiere Wahrscheinlichkeiten
Definiere jeweils die Wahrscheinlichkeit, mit denen eins der zuvor definierten Ereignisse eintritt.
$P(A)$ : Wahrscheinlichkeit, dass bei den vier Würfen genau drei mal ein Pasch fällt.
$P(C)$ : Wahrscheinlichkeit, dass drei Pasch-Würfe bei den vier Würfen hintereinander erfolgen.
$P_A (C)$ Wahrscheinlichkeit, dass drei Pasch-Würfe hintereinander erfolgen, wenn bekannt ist, dass genau drei mal ein Pasch gefallen ist.
Berechne bedingte Wahrscheinlichkeit
Dazu musst du die Formel für die Berechnung von bedingten Wahrscheinlichkeiten kennen.
$P_A(C)=\frac{P(A\cap C)}{P(A)}$
$P(A \cap C) = \,?$
Berechne $P(A \cap C)$ .
$P(A\cap C)=2\cdot \left(\frac{1}{6}\right)^3\cdot \frac{5}{6}=\frac{5}{648}=0{,}008$
$P(A) = \, ?$
Berechne $P(A)$ .
$P(A) = 4 \cdot \left(\frac{1}{6}\right)^3 \cdot \frac{5}{6} = \frac{5}{324} = 0{,}015$
$P_A(C) = \frac{P(A\cap C)}{P(A)} = \,?$
Berechne $P_A(C)$ .
$P_A(C)=\frac{P(A\cap C)}{P(A)}=\frac{2\cdot \left(\frac{1}{6}\right)^3\cdot \frac{5}{6}}{4\cdot \left(\frac{1}{6}\right)^3\cdot \frac{5}{6}}=0.5$
Ergebnis
Die Wahrscheinlichkeit, dass die drei Päsche hintereinander fallen, wenn bekannt ist, dass genau drei Päsche gefallen sind, beträgt 50 %.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Berechnen Sie, wie oft man würfeln müsste, damit die Wahrscheinlichkeit für "mindestens einmal Pasch“ mindestens 99 % beträgt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: bedingte Wahrscheinlichkeit

Definiere Ereignisse

Definiere zunächst das Ereignis, das in der Aufgabenstellung beschrieben wird.

Ereignis $(A, n)$ : Es fällt bei $n$ Würfen mindestens ein Pasch.
Ereignis $(\overline A, n)$ : Es fällt bei $n$ Würfen kein Pasch. (Gegenereignis)

Berechne Wahrscheinlichkeiten

Die Wahrscheinlichkeit, dass bei einem Wurf ein Pasch auftritt, ist $P(\text{Pasch bei einem Wurf}) = \frac{1}{6}.$ Die Wahrscheinlichkeit, dass bei einem Wurf kein Pasch auftritt, ist $P(\overline{\text{Pasch bei einem Wurf}}) = \frac{5}{6}.$

Nenne die Anzahl der Würfe $n$ . Die Wahrscheinlichkeit, dass bei $n$ Würfen kein einziger Pasch auftritt ist $P(\overline A, n) = \left( \frac{5}{6}\right)^n$ .

$\displaystyle P(A,n)$	$≥$	$\displaystyle 0{,}99$
	↓	Schreibe die Wahrscheinlichkeit über das Gegenereignis.
$\displaystyle P(\overline{A},n)$	$≤$	$\displaystyle 0{,}01$
	↓	Setze den Ausdruck für die Wahrscheinlichkeit ein.
$\displaystyle \left( \frac{5}{6}\right)^n$	$≤$	$\displaystyle 0{,}01$
	↓	Wende auf beiden Seiten den natürlichen Logarithmus an.
$\displaystyle \ln((\frac 56)^n)$	$≤$	$\displaystyle \ln 0{,}01$
	↓	Verwende Potenzregel.
$\displaystyle n\cdot\ln(\frac56)$	$≤$	$\displaystyle \ln 0{,}01$
	↓	Löse nach $n$ auf. Beachte dabei, dass $ln(\frac56)$ eine negative Zahl ist, und du deswegen das Ungleichheitszeichen umdrehen musst. Genauer erklärt ist dies im Artikel Ungleichungen lösen.
$\displaystyle n$	$≥$	$\displaystyle \frac{\ln 0{,}01}{\ln \left( \frac{5}{6}\right)} = 25.26$

Ergebnis

Man muss mindestens 26 mal würfeln.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

In einer Gruppe von 900 Personen haben sich 600 prophylaktisch gegen Grippe impfen lassen. Nach einer bestimmten Zeit wurde jedes Gruppenmitglied danach befragt, wer an einer Grippe erkrankte. Die Ergebnisse werden in einer 4-Feldtafel dargestellt.

Gruppe	$B\text{(erkrankt)}$	$\overline {B}\text{(gesund)}$	Summe
$A\text{(geimpft)}$	$60$	$540$	$600$
$\overline{A}\text{(ungeimpft)}$	$120$	$180$	$300$
Summe	$180$	$720$	$900$

Das Ereignis A sei "Person ist geimpft" und das Ereignis B: "Person erkrankt".

Berechnen Sie:

$P(A)$ , $P(B)$ , $P(A \cap B)$ , $P_A(B)$ , $P_B(A)$ sowie $P( \overline A$ $\cap B)$ und $P_{\overline{A}}(B)\$ .

Geben Sie die Bedeutung der einzelnen Ergebnisse in Textform an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeitsrechnung

Man berechnet nun nacheinander die gesuchten Wahrscheinlichkeiten. Einige kannst du auch direkt aus der Vierfeldertafel ablesen.

$P(A)$ gibt die Wahrscheinlichkeit an, mit der eine Person geimpft ist. Aus der Angabe kannst du ablesen, dass das 600 der 900 Personen sind (1. Zeile, rechts).

$\displaystyle P(A) = \frac{600} {900} = \frac{2} {3}$

$P(B)$ gibt die Wahrscheinlichkeit an, mit der eine Person erkrankt ist. Aus der Vierfeldertafel kannst du ablesen, dass es insgesamt 180 erkrankte Personen sind (1 Spalte, unten).

$\displaystyle P(B) = \frac{180} {900} = \frac{1} {5}$

$P(A \cap B)$ beschreibt die Wahrscheinlichkeit, mit der eine Person geimpft und krank ist. Aus der Vierfeldertafel kannst du ablesen, dass dies auf 60 Personen zutrifft (1 Zeile, 1 Spalte).

$\displaystyle P(A \cap B) = \frac{60} {900} = \frac{1} {15}$

$P_A(B)$ beschreibt die Wahrscheinlichkeit, dass eine Person an Grippe erkrankt, obwohl sie geimpft ist. Es geht also darum, wie groß der Anteil unter den Geimpften ist, die trotzdem erkrankt sind. Das sind $60$ von $600$ Geimpften

$P_A(B) = \dfrac{60}{600} = \dfrac{1}{10}$

Alternativ kannst du auch die Definition der bedingten Wahrscheinlichkeit benutzen: $P_A(B) = \dfrac{P(A \cap B)} {P(A)} = \dfrac{\frac{1} {15} } {\frac{2} {3}} = \frac{1} {10}$

$P_B(A)$ gibt die Wahrscheinlichkeit an, mit der eine Person geimpft ist, wenn man weiß dass sie erkrankt ist. Mit der Definition der bedingten Wahrscheinlichkeit erhältst du:

$P_B(A)= \frac{P(A \cap B)} {P(B)}$ $\displaystyle = \frac{\frac{1} {15} } {\frac{1} {5}} = \frac{1} {3}$

$P(\overline A \cap B)$ gibt die Wahrscheinlichkeit an, dass eine Person nicht geimpft wurde und krank ist. Du kannst anhand der Vierfeldertafel ablesen (1 Spalte, 2 Zeile), dass es davon 120 Personen gibt.

$\displaystyle P(\overline A \cap B) = \dfrac{120}{900}=\dfrac2{15}$

$P_{\overline{A}} (B)$ gibt die Wahrscheinlichkeit an, mit der eine zuvor nicht geimpfte Person krank ist. Von den $300$ nicht geimpften Personen sind $120$ erkrankt. Also ist die gesuchte Wahrscheinlichkeit:

$P_{\overline{A}} (B)$ $\displaystyle =\frac{120}{300}=\frac25$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

In einem Großversuch wurde ein Medikament getestet. Die Ergebnisse sind in einer Tabelle festgehalten. Dabei bedeuten:

$M$ : Medikament genommen
$\overline M$ : Placebo genommen
$G$ : Gesund geworden
$\overline G$ : nicht gesund geworden

	$G$	$\overline G$	Summe
$M$	$6312$	$87$	$6399$
$\overline M$	$312$	$4390$	$4702$
Summe	$6624$	$4477$	$11101$

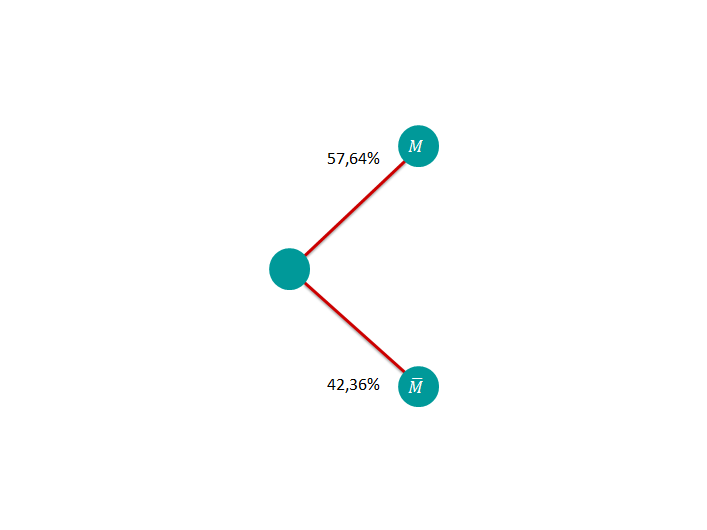
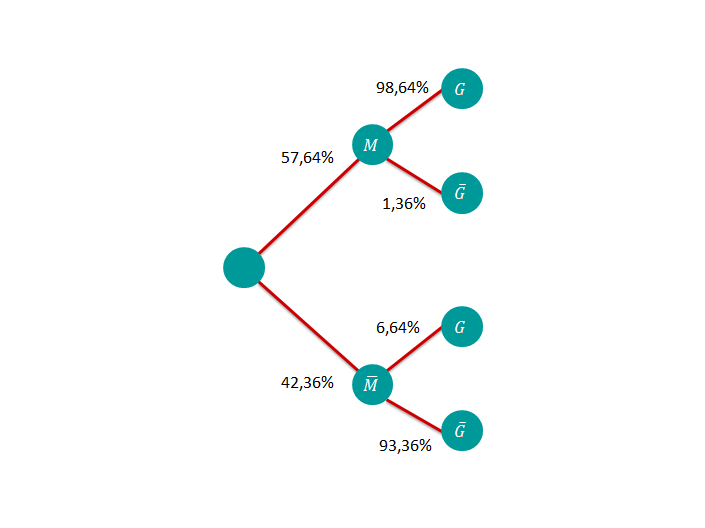
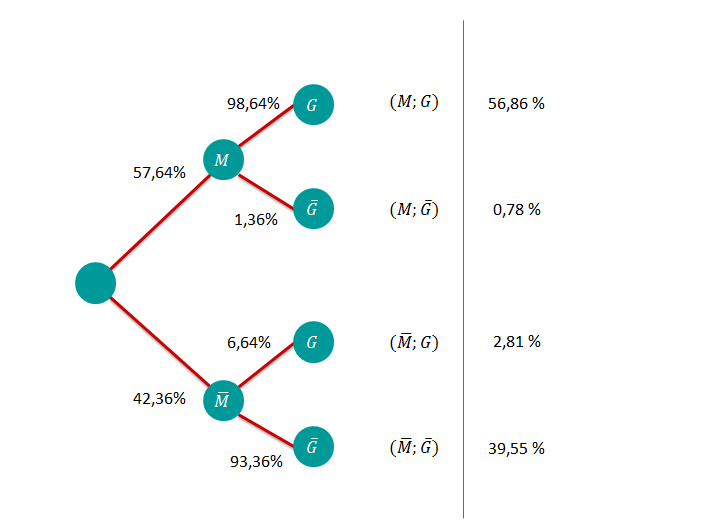
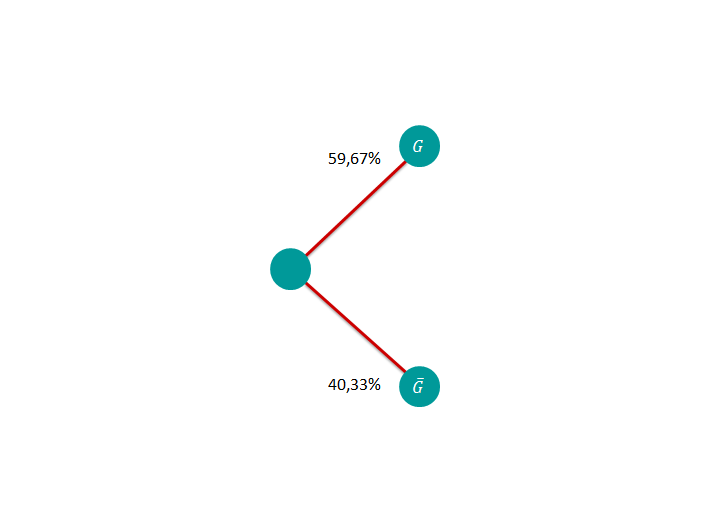
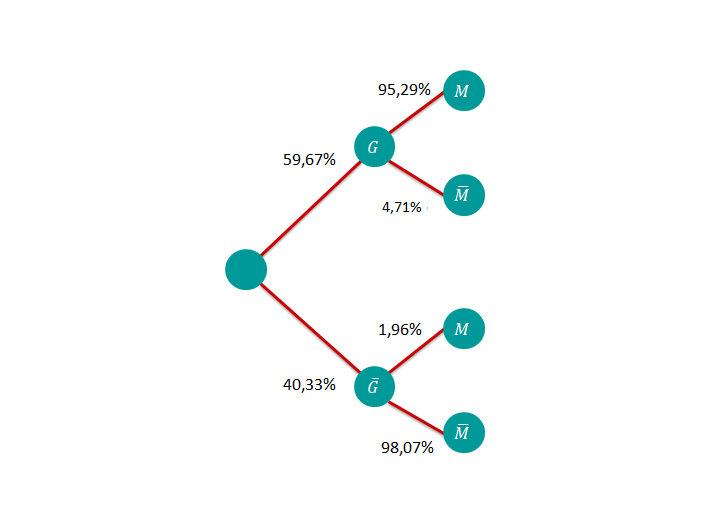
Stelle die relativen Häufigkeiten in einer Vierfeldertafel dar und stelle die dazugehörigen Baumdiagramme auf.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldertafel

Erstellen der Vierfeldertafel:

	$G$	$\overline G$	Summe
$M$	$\frac{6312}{11101}\\=0{,}5686$	$\frac{87}{11101}\\=0{,}0078$	$\frac{6399}{11101}\\=0{,}5764$
$\overline M$	$\frac{312}{11101}\\=0{,}0281$	$\frac{4390}{11101}\\=0{,}3955$	$\frac{4702}{11101}\\=0{,}4236$
Summe	$\frac{6624}{11101}\\=0{,}5967$	$\frac{4477}{11101}\\=0{,}4033$	$1$

Erstellen des 1. Baumdiagramms:

Die erste Spalte des Baumdiagramms kannst du in der Vierfeldertafel ablesen.

Die Pfadwahrscheinlichkeiten in der zweiten Spalte kannst du mithilfe der Formel für bedingte Wahrscheinlichkeit ausrechnen:

Genauso kannst du jetzt die Wahrscheinlichkeiten für $P(\overline G\vert M);P(\overline M \vert G);P(\overline M \vert\overline G)$ ausrechnen.

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

Nun kannst du das Baumdiagramm vervollständigen. Dazu musst du nur noch mithilfe der 1. Pfadregel die jeweiligen Wahrscheinlichkeiten ausrechnen

Erstellen des 2. Baumdiagramms:

Die erste Spalte des Baumdiagramms kannst du in der Vierfelder Tafel ablesen.

Die Pfadwahrscheinlichkeiten in der zweiten Spalte kannst du mithilfe der Formel für bedingte Wahrscheinlichkeit ausrechnen:

Genauso kannst du jetzt die Wahrscheinlichkeiten für $P(\overline M \vert G);P(\overline G \vert M);P(\overline M \vert\overline G)$ ausrechnen.

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

Nun kannst du das Baumdiagramm vervollständigen. Dazu musst du nur noch mithilfe der 1. Pfadregel die jeweiligen Wahrscheinlichkeiten ausrechnen

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Wie groß ist die Wahrscheinlichkeit bei einer Person, von der man weiß, dass sie das Medikament eingenommen hat, zu genesen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
Zuerst überlegt man, was für eine Wahrscheinlichkeit gesucht ist.
Man sucht die Wahrscheinlichkeit, dass eine Person genesen wird, unter der Bedingung, dass sie das Medikament eingenommen hat.
Das ist die Wahscheinlichkeit $P(G\vert M)$ .
Verwende die Definition der bedingten Wahrscheinlichkeit und ließ die Werte aus der Vierfeldertafel ab:
Alternativlösung
Da in Teilaufgabe a) schon das Baumdiagramm gezeichnet wurde, lässt sich aus diesem auch ganz einfach $\displaystyle P(G\vert M)$ ablesen. Du findest den Wert in der zweiten Ebene am obersten Zweig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Wie groß ist die Wahrscheinlichkeit bei einer Person, von der man weiß, dass sie das Placebo eingenommen hat, nicht zu genesen?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
Zuerst überlegt man sich, welche Wahrscheinlichkeit gesucht ist. Hier sucht man diejenige Wahrscheinlichkeit, mit der eine Person, von der man weiß, dass sie einen Placebo genommen hat, nicht gesund geworden ist.
Das ist $P_{\overline{M}} \overline G$ .
Verwende die Definition der bedingten Wahrscheinlichkeit und ließ dann die Werte aus der Vierfeldertafel ab.
Alternativlösung
In Teilaufgabe a) wurde schon das Baumdiagramm erstellt. Hieraus lässt sich $P_{\overline{M}} \overline G$ ablesen. Man findet den Wert in der zweiten Ebene, der unterste Zweig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

6
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
An einem Berufskolleg werden alle 674 Schüler/innen befragt, ob sie rauchen oder nicht rauchen. Das Ergebnis der Befragung sieht wie folgt aus: 82 der insgesamt 293 Schüler (männlich) gaben an zu rauchen. 250 Schülerinnen gaben an, nicht zu rauchen.
1. Stellen Sie den Sachzusammenhang in einer 4-Feldtafel dar. Verwenden Sie die Ereignisse (mit ihren Gegenereignissen):
  A: Die Person ist männlich.
  B: Die Person ist Raucher
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vierfeldtafel
  Stelle für die Ereignisse $A$ und $B$ sowie die Gegenereignisse $\overline{A}$ und $\overline B$ eine Vierfeldtafel auf.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & & & \\\hline\mathrm{\overline B} & & & \\\hline\ & & & \end{array}$
  Trage die Informationen aus der Aufgabenstellung in die Vierfeldtafel ein.
  $A \cap B$ : 82
  $A$ : 293
  $\overline A \cap \overline B$ : 250
  Gesamtanzahl Schüler/innen: 674
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & & \\\hline\mathrm{\overline B} & & 250 & \\\hline\ & 293 & & 674\end{array}$
  Ergänze die fehlenden Informationen und trage sie in die Vierfeldtafel ein.
  $A \cap \overline B$ : 293 - 82 = 211
  $\overline{A}$ : 674 - 293 = 381
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & & \\\hline\mathrm{\overline B} & 211 & 250 & \\\hline\ & 293 & 381 & 674\end{array}$
  Ergänze die restlichen fehlenden Informationen und trage sie in die Vierfeldtafel ein.
  $\overline A \cap B$ : 381 - 250 = 131
  $\overline B$ : 211 + 250 = 461
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & 293 & 381 & 674\end{array}$
  Ergänze die letzte Spalte $B$ . Prüfe, ob das Gleiche herauskommt, wenn du von der Gesamtanzahl $\overline B$ abziehst und wenn du $B \cap A$ und $B \cap \overline A$ addierst.
  $B$ : 674 - 461 = 213
  $B$ : 82 + 131 = 213
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & 293 & 381 & 674\end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Mit welcher Wahrscheinlichkeit ist eine zufällig ausgewählte Person weiblich und Nichtraucherin?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit aus relativer Häufigkeit
  Ereignis definieren
  Die gesuchten Eigenschaften sind die Kombination Ereignisse
  $\overline A$ : Person ist weiblich
  $\overline B$ : Person ist nicht Raucher(in)
  Suche also nach dem Ereignis $\overline A \cap \overline B$ .
  Lese relative Häufigkeit aus Vierfeldtafel ab
  Stelle eine Vierfeldtafel zur Aufgabe auf.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & 293 & 381 & 674\end{array}$
  Lese die Anzahl der Ereignisse $\overline A \cap \overline B$ und die Gesamtanzahl von Ereignissen in der Tabelle ab.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & \mathbf{250} & 461 \\\hline\ & 293 & 381 & \mathbf{674}\end{array}$
  Berechne nun die relative Häufigkeit, indem du die Anzahl der Ereignisse $\overline A \cap \overline B$ durch die Gesamtanzahl von Ereignissen teilst.
  Ergebnis
  Die relative Häufigkeit der weiblichen Nichtraucherinnen gibt die Wahrscheinlichkeit an, mit der eine zufällig ausgewählte Person weiblich und Nichtraucherin ist.
  Sie beträgt 37 %.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Der Schulleiter sieht eine Schülerin im Aufenthaltsraum. Mit welcher Wahrscheinlichkeit ist diese Schülerin Nichtraucherin?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: bedingte Wahrscheinlichkeit
  Es ist bereits bekannt, dass es sich bei der Person um eine Schülerin handelt. Das Ereignis $\overline A$ ist also bereits vorgegeben. Nun bestimme die Wahrscheinlichkeit, dass die Person nicht raucht ( $\overline B$ ), wenn bereits bekannt ist, dass die Person weiblich ist ( $\overline A$ ).
  Schreibe die Definition der bedingten Wahrscheinlichkeit $P_{\overline A} (\overline B)$ .
  Stelle die Vierfeldtafel zur Aufgabe auf
  Schreibe die befüllte Vierfeldtafel zur Aufgabenstellung auf.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & 293 & 381 & 674\end{array}$
  Lese die Anzahl der Ereignisse $\overline A \cap \overline B$ , $\overline A$ und die Gesamtanzahl der Ereignisse ab, um die relativen Häufigkeiten zu bestimmen.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & \mathbf{250} & 461 \\\hline\ & 293 & \mathbf{381} & \mathbf{674}\end{array}$
  Gebe die Wahrscheinlichkeiten $P(\overline A \cap \overline B)$ und $P(\overline A)$ an.
  
  Berechne nun die bedingte Wahrscheinlichkeit
  Ergebnis
  Die Wahrscheinlichkeit, dass es sich bei der Schülerin um eine Raucherin handelt, ist 66 %.
  Beachte, dass hier etwas anderes gefragt wurde als bei der Frage "Mit welcher Wahrscheinlichkeit ist eine zufällig ausgewählte Person weiblich und Nichtraucherin?".
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Untersuchen Sie, ob das Ereignis "männlich" und das Ereignis "Raucher" voneinander abhängige Ereignisse sind.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Unabhängigkeit von Ereignissen
  Prüfe Unabhängigkeit von Ereignissen
  Zwei Ereignisse $A$ und $B$ heißen stochastisch abhängig, wenn gilt: $P(A \cap B) \neq P(A) \cdot P(B).$
  Stelle Vierfeldtafel auf
  Erstelle eine Vierfeldtafel für die in der Aufgabenstellung beschriebene Situation.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & 82 & 131 & 213 \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & 293 & 381 & 674\end{array}$
  Lese aus Vierfeldtafel die Anzahl der Ereignisse $A$ , $B$ , $A \cap B$ und die Gesamtanzahl der Ereignisse ab.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ & \quad \mathrm{A} \quad& \quad\mathrm{\overline A} \quad& \ \\\hline\mathrm{B} & \mathbf{82} & 131 & \mathbf{213} \\\hline\mathrm{\overline B} & 211 & 250 & 461 \\\hline\ & \mathbf{293} & 381 & \mathbf{674}\end{array}$
  Gib die relativen Häufigkeiten und somit die Wahrscheinlichkeiten $P(A)$ , $P(B)$ und $P(A \cap B)$ an.
  Prüfe nun, ob die Ereignisse unabhängig sind.
  $P(A) \cdot P(B) = \frac{293 \cdot 213}{674^2} = \frac{62409}{454276} = 0{,}14$ $\neq 0{,}12 = P(A \cap B)$
  Ergebnis
  Die Ergebnisse "männlich" und "Raucher" sind stochastisch voneinander abhängig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7
Bei einer Sportveranstaltung wird ein Dopingtest durchgeführt. Wenn ein Sportler gedopt hat, dann fällt der Test zu 99 $\%$ positiv aus.
Hat ein Sportler aber nicht gedopt, zeigt der Test trotzdem zu 5% ein positives Ergebnis an. Aus Erfahrung weiß man, dass 20 $\%$ der Sportler gedopt sind.
1. Bestimme die Wahrscheinlichkeit, dass eine Dopingprobe positiv ausfällt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: bedingte Wahrscheinlichkeit
  Die Ereignisse
  Lege die Ereignisse fest.
  $P:=$ "Positives Testergebnis"
  $D:=$ "Sportler hat gedopt"
  Gegebenen bedingten Wahrscheinlichkeiten
  In der Angabe findest du bedingte Wahrscheinlichkeiten.
  Die Wahrscheinlichkeit, dass der Test positiv ausfällt, unter der Bedingung, dass ein Sportler gedopt hat, ist $P(P\left|D)=99\%=0{,}99\right.$ .
  Die Wahrscheinlichkeit, dass der Test positiv ausfällt, unter der Bedingung, dass ein Sportler nicht gedopt hat ist $P(P |\overline D)=5\%=0{,}05$ .
  Wahrscheinlichkeit, dass ein Sportler gedopt hat, ist $P(D)=20\%=0{,}20$ .
  Berechnung der gesuchten Wahrscheinlichkeit
  Gesucht wird die Wahrscheinlichkeit, dass der Test positiv ausfällt, also $P(P)$ .
  $P(P)=P(P\vert D)\cdot P(D)+P(P\vert\overline D)\cdot P(\overline D)$
  Rechne mit dem Gesetz der totalen Wahrscheinlichkeit die gesuchte Wahrscheinlichkeit aus. Berechne dazu zunächst die noch fehlende Wahrscheinlichkeit $P(\overline D)$ . Dies ist die Wahrscheinlichkeit des Gegenereignisses von D, also $P(\overline D)=1-P(D)$ .
  $P(P)=0{,}99\cdot0{,}20+0{,}05\cdot(1-0{,}20)$ $=0{,}198+0{,}04\\=0{,}238\\=23{,}8\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimme die Wahrscheinlichkeit, dass der Test negativ ausfällt, obwohl der Sportler gedopt hat.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: bedingte Wahrscheinlichkeit
  Gesucht ist die Wahrscheinlichkeit, dass ein gedopter Sportler ein negatives Testergebins erhält, also P $(\overline P\vert D)$ .
  Verwende einen Satz über die Summe bedingter Wahrscheinlichkeiten.
  $P(\overline P\vert D)=1-P(P\vert D)$
  $P(\overline P\vert D)=1-0{,}99=0{,}01$
  Ergebnis
  Die Wahrscheinlichkeit, dass ein gedopter Sportler ein negatives Testergebins erhält, beträgt 1 %.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Berechne die Wahrscheinlichkeit, dass ein Sportler gedopt hat, wenn seine Dopingprobe negativ ausgefallen ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: bedingte Wahrscheinlichkeit
  Die gesuchte Wahrscheinlichkeit, dass ein Sportler gedopt ist, unter der Bedingung, dass der Dopingtest negativ ausgefallen ist, ist $P(D\vert\overline P)$ .
  Der Satz von Bayes besagt:
  $P(D\vert\overline P)=\frac{P(\overline P\vert D)\cdot P(D)}{P(\overline P)}$
  Entnehme zur Berechnung von $P(D\vert\overline P)$ aus den Teilaufgaben a) und b) die schon berechneten Wahrscheinlichkeiten $P(\overline{P}\vert D)$ und $P(D)$ . Berechne noch $P(\overline P)$ über das Gegenereignis.
  $P(\overline P)=1-P(P)=1-0{,}238=0{,}762$
  Setze nun die benötigten Angaben ein.
  $P(D\vert\overline P)=\frac{0{,}01\cdot0{,}20}{0{,}762}=0{,}0026$
  Ergebnis
  Die Wahrscheinlichkeit, dass ein Sportler gedopt ist, unter der Bedingung, dass der Dopingtest negativ ausgefallen ist, beträgt 0,26 %.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Es soll die Beliebtheit einer Fernsehsendung überprüft werden. Eine Blitzumfrage hatte folgendes Ergebnis:
30% der Zuschauer, die die Sendung gesehen hatten, waren 25 Jahre und jünger. Von diesen hatten 50% und von den übrigen Zuschauern (über 25 Jahre) hatten 80% eine positive Meinung.
1. Stellen Sie den Sachzusammenhang in einer 4-Feldtafel da. Verwenden Sie die Ereignisse (mit ihren Gegenereignissen):
  A: Der Zuschauer ist 25 Jahre alt und jünger.
  B: Der Zuschauer hat eine positive Meinung über die Sendung.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: 4-Feldtafel
  Definiere Ereignisse
  Definiere die Ereignisse, die in der Aufgaben genannt wurden.
  $A$ : Der Zuschauer oder die Zuschauerin ist 25 Jahre alt und jünger.
  $\overline A$ : Der Zuschauer oder die Zuschauerin ist älter als 25 Jahre.
  $B$ : Der Zuschauer oder die Zuschauerin hat eine positive Meinung über die Sendung.
  $B$ : Der Zuschauer oder die Zuschauerin hat eine negative Meinung über die Sendung.
  Berechne relative Häufigkeiten
  Entnehme aus der Aufgabenstellung die bereits angegebenen Wahrscheinlichkeiten.
  Gib die Wahrscheinlichkeit an, dass ein zufällig gezogener Zuschauer 25 Jahre alt und jünger ist.
  $P(A) = 0.3$
  Verwende das Gegenereignis um die Wahrscheinlichkeit zu bestimmen, dass ein zufällig gezogener Zuschauer älter als 25 Jahre alt ist.
  $P(\overline A) = 1- 0.3 = 0.7$
  Gib die Wahrscheinlichkeit an, dass ein zufällig gezogener Zuschauer 25 Jahre alt oder jünger ist und eine positive Meinung hat.
  $P(A \cap B) = 0.3 \cdot 0.5 = 0{,}15$
  Gib die Wahrscheinlichkeit an, dass ein zufällig gezogener Zuschauer 25 Jahre alt oder jünger ist und eine negative Meinung hat.
  $P(A \cap \overline B) = 0.3 \cdot 0.5 = 0{,}15$
  Gib die Wahrscheinlichkeit an, dass ein zufällig gezogener Zuschauer älter als 25 Jahre alt ist und eine positive Meinung hat.
  $P(\overline A \cap B) = 0.8 \cdot 0.7 = 0{,}56$
  Erstelle eine Vierfelder-Tafel auf
  Stelle eine leere Vierfelder-Tafel auf.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{A}\quad & \quad \mathrm{\overline A}\quad & \ \\\hline\mathrm{B} & & & \\\hline\mathrm{\overline B} & & & \\\hline\ & & & 1 \end{array}$
  Trage die zuvor ermittelten Wahrscheinlichkeiten in die Tafel ein.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{B}\quad & \quad \mathrm{\overline B}\quad & \ \\\hline\mathrm{A} & 0{,}15 & 0{,}15 & \\\hline\mathrm{\overline A} & 0{,}56 & & \\\hline\ & & & 1 \end{array}$
  Fülle weitere Felder der Tafel.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{B}\quad & \quad \mathrm{\overline B}\quad & \ \\\hline\mathrm{A} & 0{,}15 & 0{,}15 & 0{,}3\\\hline\mathrm{\overline A} & 0{,}56 & & \\\hline\ & 0{,}71 & & 1 \end{array}$
  Fülle die nächsten Felder der Tafel.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{B}\quad & \quad \mathrm{\overline B}\quad & \ \\\hline\mathrm{A} & 0{,}15 & 0{,}15 & 0{,}3\\\hline\mathrm{\overline A} & 0{,}56 & & \\\hline\ & 0{,}71 & 0{,}29& 1 \end{array}$
  Fülle die letzten Felder der Tafel.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{B}\quad & \quad \mathrm{\overline B}\quad & \ \\\hline\mathrm{A} & 0{,}15 & 0{,}15 & 0{,}3\\\hline\mathrm{\overline A} & 0{,}56 & 0{,}14 & 0{,}7\\\hline\ & 0{,}71 & 0{,}29& 1 \end{array}$
  Auflistung der Wahrscheinlichkeiten in der Tabelle
  $P\left(A\right)=30\%$ , da 30% der Zuschauer jünger als 25 Jahre sind (siehe Text).
  $P\left(\overline A\right)=1-P\left(A\right)=100\%-30\%=70\%$ , da Gegenereignis .
  $P\left(A\cap B\right)=P\left(A\right)\cdot P\left(B\right)=0{,}3\cdot0{,}5=0{,}15=15\%$
  $P\left(A\cap\overline B\right)=P\left(A\right)-P\left(A\cap B\right)=30\%-15\%=15\%$
  $P\left(\overline A\cap B\right)=P\left(\overline A\right)\cdot P\left(B\right)=0{,}8\cdot0{,}7=0{,}56=56\%$
  $P\left(\overline A\cap\overline B\right)=P\left(\overline A\right)-P\left(\overline A\cap B\right)=70\%-56\%=14\%$
  $P\left(A\cap B\right)+P\left(\overline A\cap B\right)=P\left(B\right)=15\%+56\%=71\%$
  $P\left(A\cap\overline B\right)+P\left(\overline A\cap\overline B\right)=P\left(\overline B\right)=15\%+14\%=29\%$
  Ergebnis
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{B}\quad & \quad \mathrm{\overline B}\quad & \ \\\hline\mathrm{A} & 0{,}15 & 0{,}15 & 0{,}3\\\hline\mathrm{\overline A} & 0{,}56 & 0{,}14 & 0{,}7\\\hline\ & 0{,}71 & 0{,}29& 1 \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
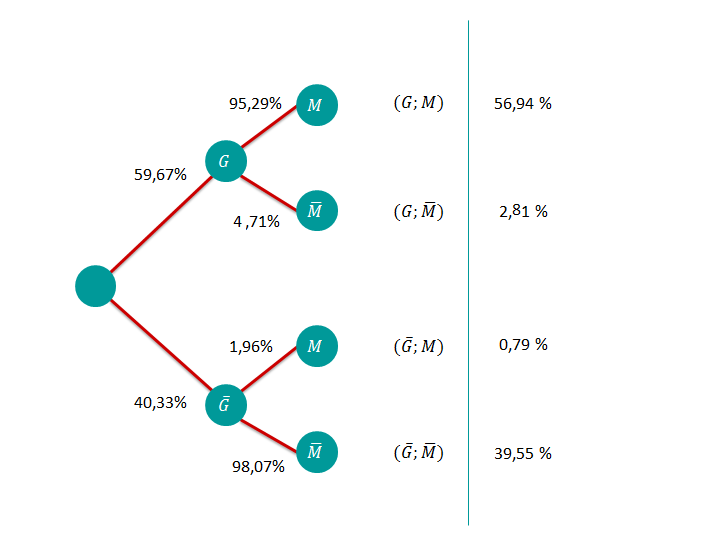
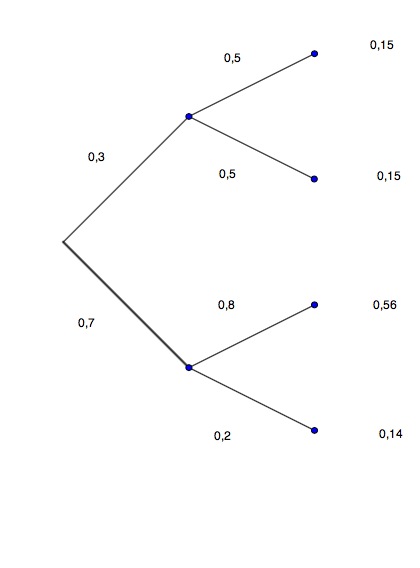
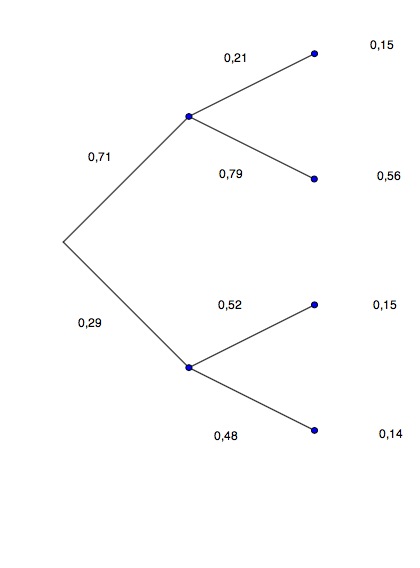
2. Zeichnen Sie das Baumdiagramm und den inversen Baum.
  Bestimmen Sie alle Pfadwahrscheinlichkeiten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zeichne das Baumdiagramm
  Zeichne das Baumdiagramm
  Berechne alle Pfadwahrscheinlichkeiten
  Verwende die Vierfeldtafel, um alle Pfadwahrscheinlichkeiten anzugeben oder gegebenenfalls zu berechnen.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{B}\quad & \quad \mathrm{\overline B}\quad & \ \\\hline\mathrm{A} & 0{,}15 & 0{,}15 & 0{,}3\\\hline\mathrm{\overline A} & 0{,}56 & 0{,}14 & 0{,}7\\\hline\ & 0{,}71 & 0{,}29& 1 \end{array}$
  Lese alle benötigten Wahrscheinlichkeiten aus der Vierfeldtafel ab.
  $P(A) = 0{,}3$
  $P(\overline A) = 0{,}7$
  $P(B) = 0{,}71$
  $P(\overline B) = 0{,}29$
  $P(A \cap B) = 0{,}15$
  $P(A \cap \overline B) = 0{,}15$
  $P(\overline A \cap B) = 0{,}56$
  $P(\overline A \cap \overline B) = 0{,}14$
  Berechne nun die bedingten Wahrscheinlichkeiten, die du für das Baumdiagramm benötigst.
  $P_A (B) = \frac{P(A \cap B )}{P(A)} = \frac{0{,}15}{0{,}3} = 0{,}5$
  $P_A (\overline B) = \frac{P(A \cap \overline B )}{P(A)} = \frac{0{,}15}{0{,}3} =0{,}5$
  $P_{\overline A} (B) = \frac{P(\overline A \cap B )}{P(\overline A)} = \frac{0{,}56}{0{,}7} = 0{,}8$
  $P_{\overline A} (\overline B) = \frac{P(\overline A \cap \overline B )}{P(\overline A)} = \frac{0{,}14}{0{,}7} = 0{,}2$
  $P_B (A) = \frac{P(A \cap B )}{P(B)} = \frac{0{,}15}{0{,}71} = 0{,}21$
  $P_B (\overline A) = \frac{P(\overline A \cap B )}{P(B)} = \frac{0{,}56}{0{,}71} = 0{,}79$
  $P_{\overline B} (A) = \frac{P(A \cap \overline B )}{P(\overline B)} =\frac{0{,}15}{0{,}29} = 0{,}52$
  $P_{\overline B} (\overline A) = \frac{P(\overline A \cap \overline B )}{P(\overline B)} = \frac{0{,}14}{0{,}29} = 0{,}48$
  Zeichne das Baumdiagramm
  Zeichne nun mit den ermittelten Pfadwahrscheinlichkeiten das Baumdiagramm. Ordne dabei die Ereignisse in der Reihenfolge $A$ und dann $B$ an.
  Zeichne das inverse Baumdiagramm
  Zeichne nun mit den ermittelten Pfadwahrscheinlichkeiten das inverse Baumdiagramm. Ordne dabei die Ereignisse in der Reihenfolge $B$ und dann $A$ an.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Wie viel % der Zuschauer, von denen man weiß, dass sie eine positive Meinung über die Sendung hatten, waren älter als 25 Jahre?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit
  Bedingung: positive Meinung
  Ereignis : älter als 25 Jahre
  ${\mathrm P}_\mathrm B\left(\overline{\mathrm A}\right)=\frac{\mathrm P\left(\overline{\mathrm A}\cap\mathrm B\right)}{\mathrm P\left(\mathrm B\right)}$
  Bedingte Wahrscheinlichkeit
  Berechne die
  Schnittmenge der
  beiden Ereignisse .
  $\mathrm P\left(\overline{\mathrm A}\cap\mathrm B\right)\rightarrow\mathrm P(\mathrm{positive}\;\mathrm{Meinung}\;\mathrm{und}\;\mathrm{älter}\;\mathrm{als}\;25\;\mathrm{Jahre})=0{,}7\cdot0{,}8$
  Berechne die Summe der
  günstigen
  Wahrscheinlichkeiten .
  $\mathrm P\left(\mathrm B\right)\rightarrow\mathrm P(\mathrm{postive}\;\mathrm{Meinung})=0{,}3\cdot0{,}5+0{,}7\cdot0{,}8$
  $\def\arraystretch{1.25} \begin{array}{l}=\mathrm P\left(\mathrm{jünger}\;\mathrm{als}\;25\;\mathrm{Jahre}\;\mathrm{und}\;\mathrm{positive}\;\mathrm{Meinung}\right)\\\;\;\;+\mathrm P\left(\mathrm{älter}\;\mathrm{als}\;25\;\mathrm{Jahre}\;\mathrm{und}\;\mathrm{positive}\;\mathrm{Meinung}\right)\end{array}$
  Setze in die obige Formel ein.
  ${\mathrm P}_{\mathrm{positive}\;\mathrm{Meiniung}}\left(\mathrm{älter}\;\mathrm{als}\;25\;\mathrm{Jahre}\right)=\frac{\mathrm P(\mathrm{positive}\;\mathrm{Meinug}\;\mathrm{und}\;\mathrm{älter}\;\mathrm{als}\;25\;\mathrm{Jahre})}{\mathrm P(\mathrm{positive}\;\mathrm{Meinung})\;}=$
  ${\mathrm P}_{\mathrm{positive}\;\mathrm{Meiniung}}\left(\mathrm{älter}\;\mathrm{als}\;25\;\mathrm{Jahre}\right)=\frac{0{,}7\cdot0{,}8}{0{,}3\cdot0{,}5+0{,}7\cdot0{,}8}=$
  Dividiere .
  ${\mathrm P}_{\mathrm{positive}\;\mathrm{Meiniung}}\left(\mathrm{älter}\;\mathrm{als}\;25\;\mathrm{Jahre}\right)\approx0{,}789$
  Rechne in Prozent um.
  $\approx78{,}9\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Wie viel % der Zuschauer, von denen man weiß, dass sie älter als 25 Jahre sind, hatten keine positive Meinung über die Sendung?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: bedingte Wahrscheinlichkeit
  Gegeben sind die Ereignisse
  $A$ : Der Zuschauer ist 25 Jahre alt oder jünger.
  $B$ : Der Zuschauer hat eine positive Meinung über die Sendung.
  Gesucht ist dann die bedingte Wahrscheinlichkeit $P_{\overline A}(\overline B)$ .
  Für die Lösung gibt es zwei verschiedene Möglickkeiten.
  Gegenwahrscheinlichkeit
  Nach Aufgabenstellung haben 80% der über 25-Jährigen eine positive Meinung, d. h.
  Die gesuchte Wahrscheinlichkeit ergibt sich also als Gegenwahrscheinlichkeit:
  Vierfeldertafel
  Das Ergebnis lässt sich auch aus der Vierfeldertafel ablesen:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Überprüfen Sie durch Rechnung ob das Ereignis B unabhängig von Ereignis A ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Unabhängigkeit von Ereignissen
  Überprüfe durch Rechnung die Unabhängigkeit der Ereignisse. Zwei Ereignisse $A$ und $B$ sind unabhängig, falls gilt $P_B(A) = P(A)$ .
  Lese die Wahrscheinlichkeiten am Baumdiagramm oder an der Vierfeld-Tafel ab.Dabei ist $P_B(A) = 0{,}21$ und $P(A) = 0{,}3$ . Die Wahrscheinlichkeiten sind also ungleich und somit die Ereignisse abhängig voneinander.
  Ergebnis
  Das Ereignis $B$ ist abhängig vom Ereignis $A$ . Das bedeutet, die positive Meinung über die Fernsehsendung ist vom Alter der Zuschauer abhängig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
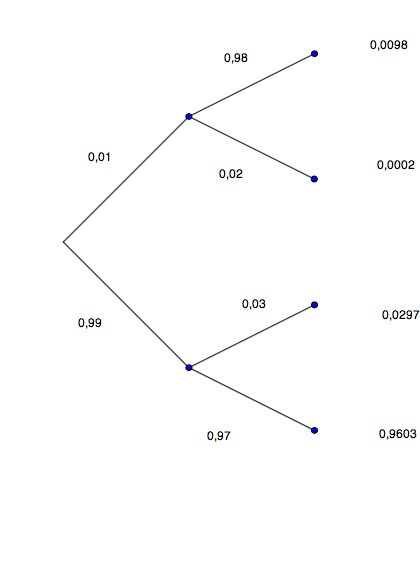
In einem Land der Dritten Welt leiden 1% der Menschen an einer bestimmten Infektionskrankheit. Ein Test zeigt die Krankheit bei den tatsächlich Erkrankten zu 98% korrekt an. Leider zeigt der Test auch 3% der Gesunden als erkrankt an.
1. Stellen Sie den Sachzusammenhang in einer 4-Feldtafel da. Verwenden Sie die Ereignisse (mit ihren Gegenereignissen):
  K: Die getestete Person ist krank.
  T: Testergebnis ist positiv (Person wurde als krank getestet).
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: 4-Feldtafel
  Definiere Ereignisse
  Definiere die Ereignisse, die in der Aufgaben genannt wurden.
  $K$ : Die Person ist krank
  $\overline K$ : Die Person ist gesund
  $T$ : Der Test fällt bei der Person positiv aus (Nach Aussage des Tests sei Person krank)
  $\overline T$ : Der Test fällt bei der Person negativ aus (Nach Aussage des Tests sei Person gesund)
  Berechne Wahrscheinlichkeiten
  Entnehme der Aufgabenstellung bekannte Wahrscheinlichkeiten.
  Gib die Wahrscheinlichkeit an, mit der eine zufällig ausgewählte Person erkrankt ist.
  $P(K) = 0{,}01$ $P(\overline K) = 0{,}99$
  Gib die Wahrscheinlichkeit an, mit der eine Person erkrankt ist und bei ihr der Test positiv ausfällt.
  $P(K \cap T) = 0{,}01 \cdot 0{,}98 = 0{,}0098$
  Gib die Wahrscheinlichkeit an, mit der eine Person gesund ist und bei ihr der Test trotzdem positiv ausfällt.
  $P(\overline K \cap T) = 0{,}99 \cdot 0{,}03 = 0{,}0297$
  Zeichne eine Vierfeld-Tafel
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{K}\quad & \quad \mathrm{\overline K}\quad & \ \\\hline\mathrm{T} & & & \\\hline\mathrm{\overline T} & & & \\\hline\ & & & 1 \end{array}$
  Trage die eben berechneten Informationen als Wahrscheinlichkeiten in die Vierfeld-Tafel ein.
  Beachte, dass sich die Wahrscheinlichkeiten insgesamt zu 1 addieren.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{K}\quad & \quad \mathrm{\overline K}\quad & \ \\\hline\mathrm{T} & 0{,}0098 & 0{,}0297 & \\\hline\mathrm{\overline T} & & & \\\hline\ & 0{,}01 & 0{,}99& 1 \end{array}$
  Berechne die fehlenden Informationen.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{K}\quad & \quad \mathrm{\overline K}\quad & \ \\\hline\mathrm{T} & 0{,}0098 & 0{,}0297 & 0{,}0395 \\\hline\mathrm{\overline T} & 0{,}0002 & 0{,}9603 & 0{,}9605 \\\hline\ & 0{,}01 & 0{,}99& 1 \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
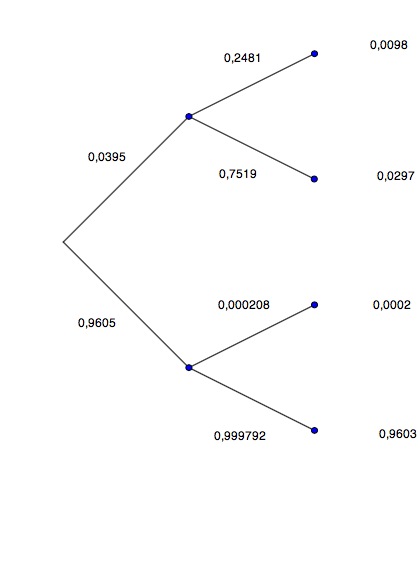
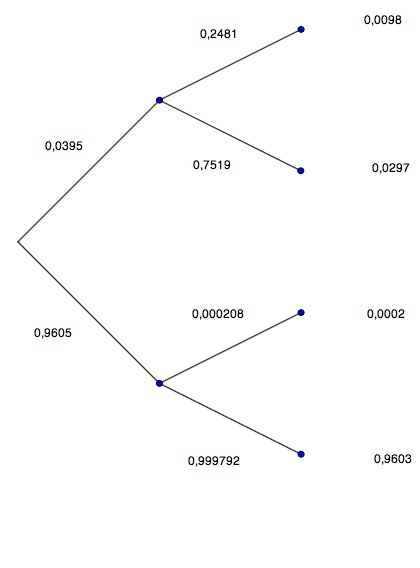
2. Zeichnen Sie das Baumdiagramm und den inversen Baum. Bestimmen Sie alle Pfadwahrscheinlichkeiten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm
  Zeichne das Baumdiagramm
  Berechne alle Pfadwahrscheinlichkeiten
  Verwende die Vierfeldtafel, um alle Pfadwahrscheinlichkeiten anzugeben oder gegebenenfalls zu berechnen.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{K}\quad & \quad \mathrm{\overline K}\quad & \ \\\hline\mathrm{T} & 0{,}0098 & 0{,}0297 & 0{,}0395 \\\hline\mathrm{\overline T} & 0{,}0002 & 0{,}9603 & 0{,}9605 \\\hline\ & 0{,}01 & 0{,}99& 1 \end{array}$
  Lese alle benötigten Wahrscheinlichkeiten aus der Vierfeldtafel ab.
  $P(K) = 0{,}01$
  $P(\overline K) = 0{,}99$
  $P(T) = 0{,}0395$
  $P(\overline T) = 0{,}9605$
  $P(K \cap T) = 0{,}0098$
  $P(K \cap \overline T) = 0{,}0002$
  $P(\overline K \cap T) = 0{,}0297$
  $P(\overline K \cap \overline T) = 0{,}9603$
  Berechne nun die bedingten Wahrscheinlichkeiten, die du für das Baumdiagramm benötigst.
  $P_K (T) = \frac{P(K \cap T )}{P(K)} = \frac{0{,}0098}{0{,}01} = 0{,}98$
  $P_K (\overline T) = \frac{P(K \cap \overline T )}{P(K)} = \frac{0{,}0002}{0{,}01} =0{,}02$
  $P_{\overline K} (T) = \frac{P(\overline K \cap T )}{P(\overline K)} = \frac{0{,}0297}{0{,}99} = 0{,}03$
  $P_{\overline K} (\overline T) = \frac{P(\overline K \cap \overline T )}{P(\overline K)} = \frac{0{,}9603}{0{,}99} = 0{,}97$
  $P_T (K) = \frac{P(K \cap T )}{P(T)} = \frac{0{,}0098}{0{,}0395} = 0{,}2481$
  $P_T (\overline K) = \frac{P(\overline K \cap T )}{P(T)} = \frac{0{,}0297}{0{,}0395} = 0{,}7519$
  $P_{\overline T} (K) = \frac{P(K \cap \overline T )}{P(\overline T)} =\frac{0{,}0002}{0{,}9605} = 0{,}000208$
  $P_{\overline T} (\overline K) = \frac{P(\overline K \cap \overline T )}{P(\overline T)} = \frac{0{,}9603}{0{,}9605} = 0{,}999792$
  Zeichne das Baumdiagramm
  Zeichne nun mit den ermittelten Pfadwahrscheinlichkeiten das Baumdiagramm. Ordne dabei die Ereignisse in der Reihenfolge "krank" - "nicht krank" und "Test positiv" - "Test negativ" an.
  Zeichne das inverse Baumdiagramm
  Zeichne nun mit den ermittelten Pfadwahrscheinlichkeiten das inverse Baumdiagramm. Ordne dabei die Ereignisse in der Reihenfolge "Test positiv" - "Test negativ" und "krank" - "nicht krank" an.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Mit welcher Wahrscheinlichkeit zeigt der Test bei einer zufällig ausgewählten Person ein positives Ergebnis?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechne die Wahrscheinlichkeit
  Berechne die Wahrscheinlichkeit, mit der der Test bei einer zufällig ausgewählten Person ein positives Ergebnis zeigt.
  Betrachte das Baumdiagramm.
  Summiere die Pfadwahrscheinlichkeiten $P(K \cap T)$ und $P(\overline K \cap T)$ .
  $P(K \cap T) + P(\overline K \cap T) = 0{,}0098 + 0{,}0297 = 0{,}0395$
  Rechne in Prozent um.
  $=3{,}95\%$
  Ergebnis
  Bei einer zufällig ausgewählten Person zeigt der Test mit einer Wahrscheinlichkeit von 3,95 % ein positives Ergebnis an.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Mit welcher Wahrscheinlichkeit ist eine positiv getestete Person auch tatsächlich krank? Kommentieren Sie das Ergebnis.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ermittle die Wahrscheinlichkeit
  Lese die bedingte Wahrscheinlichkeit ab
  Ermittle die Wahrscheinlichkeit, mit der eine Person auch tatsächlich krank ist, wenn bekannt ist, dass der Test bei ihr positiv war.
  Betrachte das Baumdiagramm.
  Betrachte den Pfad $T$ und lese die bedingte Wahrscheinlichkeit $P_T{K} = \frac{P(T\cap K)}{P(T)} = 0{,}2481$ ab.
  Ergebnis
  Eine Person, von der bekannt ist, dass der Test positiv ausgefallen ist, ist mit einer Wahrscheinlichkeit von 24,81 % auch tatsächlich krank.
  Kommentar: Das Ergebnis von ca. 25% ist nicht zufriedenstellend. Nur 25% aller positiv getesteten sind tatsächlich erkrankt. Das bedeutet, dass ca. 75% der positiv getesteten gesund sind. Es wäre wünschenswert, dass der Test verbessert wird.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Mit welcher Wahrscheinlichkeit ist eine als negativ getestete Person gesund? Kommentieren Sie das Ergebnis.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Ermittle die Wahrscheinlichkeit
  Lese die bedingte Wahrscheinlichkeit ab
  Ermittle die Wahrscheinlichkeit, mit der eine Person gesund ist, wenn bekannt ist, dass der Test bei ihr negativ war.
  Betrachte das Baumdiagramm.
  Betrachte den Pfad $\overline T$ und lese die bedingte Wahrscheinlichkeit $P_{\overline T} {\overline K} = \frac{P(\overline T \cap \overline K)}{P(\overline T)} = 0{,}999792$ ab.
  Ergebnis
  Eine Person, von der man weiß, dass sie negativ getestet wurde, ist mit einer Wahrscheinlichkeit von 0,999792 auch tatsächlich gesund.
  Kommentar: In diesem Fall ist das Ergebnis von ca. 99,98% sehr zufriedenstellend. Nur ca. 0,02% der als negativ getesteten Personen sind tatsächlich krank.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Mehr Abiturientinnen als Abiturienten:

52,4% der 244600 Jugendlichen, die am Ende des vergangenen Schuljahres ihre Schule mit der allgemeinen Hochschulreife verließen, waren Frauen. In den neuen Ländern und in Berlin liegt der Frauenanteil mit 59,1% deutlich höher als im früheren Bundesgebiet (50,8%).

Stellen Sie eine 4-Feldtafel auf, die diesen Sachzusammenhang beschreibt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: 4-Feldertafel

Stelle eine 4-Feldertafel auf

Definiere Ereignisse

Definiere die Ereignisse, die in der Aufgaben genannt wurden.

$A$ : Person kommt aus den alten Bundesländern (Westdeutschland)
$\overline A$ : Person kommt aus den neuen Bundesländern oder Berlin (Ostdeutschland)
$B$ : Person ist eine Frau
$\overline B$ : Person ist ein Mann

Berechne absolute Häufigkeiten

Berechne Anzahl der Ereignisse "Person ist weiblich".

$0{,}524 \cdot 244600 = 128170{,}4 \approx 128170$

Berechne Anzahl der Ereignisse "Person ist männlich".

$244600 - 128170 = 116430$

Definiere Anzahl der Absolventen aus dem Westen und aus dem Osten

$x$ : Anzahl der Absolventen West $244600-x$ : Anzahl der Absolventen Ost

Definiere Anzahl der weiblichen Absolventen aus jeweils Westen und Osten

$0{,}508 \cdot x$ : Anzahl der weiblichen Absolventen West

$0{,}591 \cdot (244600 - x)$ : Anzahl der weiblichen Absolventen West

Gib die Anzahl der weiblichen Absolventinnen als Summe der Absolventinnen aus Ost und West an.

$0{,}508 \cdot x + 0{,}591 \cdot (244600-x) = 128170$

Löse nach x auf und berechne so die Anzahl der Absolventen in Westdeutschland

$x = 197453$

Berechne damit jeweils die Anzahl der Absolventen und Absolventinnen in jeweils Ost und West.

	Zusammenfassung
weiblich West	$0{,}508 \cdot 197453 = 100306$
weiblich Ost	$128170 - 100306 = 27864$
männlich West	$197453 - 100306 = 97147$
männlich Ost	$116430 - 97147 = 19283$

Stelle eine Vierfeldertafel auf

Zeichne als erstes eine leere Vierfeldertafel.

$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{A}\quad & \quad \mathrm{\overline A}\quad & \ \\\hline\mathrm{B} & & & \\\hline\mathrm{\overline B} & & & \\\hline\ & & & \end{array}$

Trage die zuvor berechneten Informationen in die Vierfeldertafel ein.

$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{A}\quad & \quad \mathrm{\overline A}\quad & \ \\\hline\mathrm{B} & 100306 & 27864 & \\\hline\mathrm{\overline B} & 97147 & 19283 & \\\hline\ & & & 244600 \end{array}$

Ergänze die fehlenden Werte.

$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{A}\quad & \quad \mathrm{\overline A}\quad & \ \\\hline\mathrm{B} & 100306 & 27864 & 128170\\\hline\mathrm{\overline B} & 97147 & 19283 & 116430 \\\hline\ & 197453& 47147 &244600 \end{array}$

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

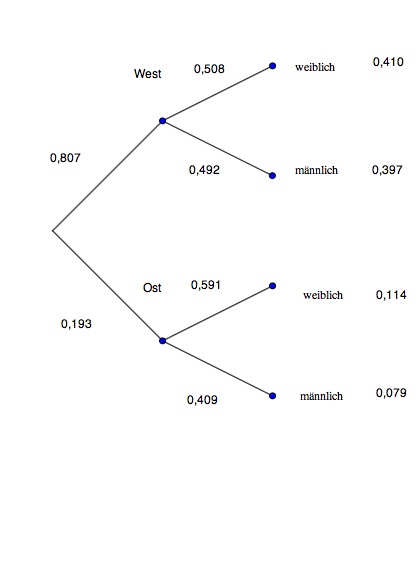
Zeichnen Sie ein Baumdiagramm mit dem 1. Merkmal "Herkunft" (Ost, West) und dem 2. Merkmal "Geschlecht" (männlich, weiblich).
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm
Zeichne ein Baumdiagramm
Ermittle Wahrscheinlichkeiten
Schreibe die zum Zeichnen des Baumdiagramms benötigten Wahrscheinlichkeiten auf. Verwende dazu die Informationen aus der Vierfeldertafel aus der ersten Teilaufgabe.
$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{A}\quad & \quad \mathrm{\overline A}\quad & \ \\\hline\mathrm{B} & 100306 & 27864 & 128170\\\hline\mathrm{\overline B} & 97147 & 19283 & 116430 \\\hline\ & 197453& 47147& 244600 \end{array}$
Berechne nun die benötigten relativen Häufigkeiten.
$P(A) = \frac{197453}{244600} = 0{,}807$
$P (\overline A) = \frac{47147}{244600} = 0{,}193$
$P(A \cap B) = \frac{100306}{244600} = 0{,}410$
$P(A \cap \overline B) = \frac{97147}{244600} = 0{,}397$
$P(\overline A \cap B) = \frac{27864}{244600} = 0{,}114$
$P(\overline A \cap B) = \frac{19283}{244600} = 0{,}079$
$P_{A} (B) = \frac{P(A \cap B)}{P(A)} = \frac{100306}{197453} = 0{,}508$
$P_{A} (\overline B) = \frac{P(A \cap \overline B)}{P(A)} = \frac{97147}{197453} = 0{,}492$
$P_{\overline A} (B) = \frac{P(\overline A \cap B)}{P(\overline A)} = \frac{27864}{47147} = 0{,}591$
$P_{\overline A} (\overline B) = \frac{P(\overline A \cap \overline B)}{P(\overline A)} = \frac{19283}{47147} = 0{,}409$
Zeichne das Baumdiagramm
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zeichnen Sie ein Baumdiagramm mit dem 1. Merkmal "Geschlecht" (männlich, weiblich) und dem 2. Merkmal "Herkunft" (Ost, West).
Für diese Aufgabe benötigst Du folgendes Grundwissen: Baumdiagramm
Zeichne ein Baumdiagramm
Ermittle Wahrscheinlichkeiten
Schreibe die zum Zeichnen des Baumdiagramms benötigten Wahrscheinlichkeiten auf. Verwende dazu die Informationen aus der Vierfeldertafel aus der ersten Teilaufgabe.
$\def\arraystretch{1.25} \begin{array}{c|c|c|c}\ &\quad \mathrm{A}\quad & \quad \mathrm{\overline A}\quad & \ \\\hline\mathrm{B} & 100306 & 27864 & 128170\\\hline\mathrm{\overline B} & 97147 & 19283 & 116430 \\\hline\ & 197453& 47147& 244600 \end{array}$
Berechne nun die benötigten relativen Häufigkeiten.
$P(B) = \frac{128170}{244600} = 0{,}524$
$P (\overline B) = \frac{116430}{244600} = 0{,}476$
$P(A \cap B) = \frac{100306}{244600} = 0{,}410$
$P(A \cap \overline B) = \frac{97147}{244600} = 0{,}397$
$P(\overline A \cap B) = \frac{27864}{244600} = 0{,}114$
$P(\overline A \cap B) = \frac{19283}{244600} = 0{,}079$
$P_{B} (A) = \frac{P(A \cap B)}{P(B)} = \frac{100306}{128170} = 0{,}783$
$P_{B} (\overline A) = \frac{P(\overline A \cap B)}{P(B)} = \frac{27864}{128170} = 0{,}217$
$P_{\overline B} (A) = \frac{P(A \cap \overline B)}{P(\overline B)} = \frac{97147}{116430} = 0{,}834$
$P_{\overline B} (\overline A) = \frac{P(\overline A \cap \overline B)}{P(\overline B)} = \frac{19283}{116430} = 0{,}166$
Zeichne das Baumdiagramm
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Aus der Gesamtheit aller Abiturientinnen und Abiturienten des betrachteten Jahrgangs wurde eine Person zufällig ausgewählt.
(1) Mit welcher Wahrscheinlichkeit stammt diese Person aus Ostdeutschland?
(2) Mit welcher Wahrscheinlichkeit ist die ausgewählte Person eine Frau?
(3) Falls diese Person aus Ostdeutschland kommt, mit welcher Wahrscheinlichkeit ist dies ein Mann?
(4) Falls diese Person eine Frau ist, mit welcher Wahrscheinlichkeit stammt sie aus Westdeutschland?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit berechnen
Teilaufgabe 1
Berechne die Wahrscheinlichkeit, dass diese Person aus Ostdeutschland stammt.
Die Wahrscheinlichkeit beträgt $P(\overline A) = \frac{47147}{244600} = 0{,}193$ .
Teilaufgabe 2
Berechne die Wahrscheinlichkeit, dass diese Person eine Frau ist.
Die Wahrscheinlichkeit beträgt $P(B) = \frac{128170}{244600} = 0{,}524$ .
Teilaufgabe 3
Berechne die Wahrscheinlichkeit mit der die Person ein Mann ist, wenn bekannt ist, dass sie aus Ostdeutschland kommt.
Die Wahrscheinlichkeit ist $P_{\overline A} (\overline B) = \frac{P(\overline A \cap \overline B)}{P(\overline A)} = \frac{19283}{47147} = 0{,}409$ .
Teilaufgabe 4
Berechne die Wahrscheinlichkeit mit der diese Person aus Westdeutschland stammt, wenn bekannt ist, dass sie eine Frau ist.
Die Wahrscheinlichkeit ist $P_B (A) = \frac{P(A \cap B)}{P(B)} = \frac{100306}{128170} = 0{,}783$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Gegeben sind Ereignisse A, B mit $P\left(A\right)=0{,}72$ , $P\left(A\cap B\right)=0{,}18$ , $P\left(A\cup B\right)=0{,}832$ . Wie groß sind dann die bedingten Wahrscheinlichkeiten $P_B\left(A\right)$ und $P_{\overline{A}}\left(B\right)$ ?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bedingte Wahrscheinlichkeit berechnen

Berechne die bedingte Wahrscheinlichkeit $P_B(A)$

Definition von bedingter Wahrscheinlichkeit

\displaystyle P(M\vert \overline G)=\dfrac{P(M\cap \overline G)}{P(M)}\approx\dfrac{0{,}78 \,\%}{57{,}64\,\%}\approx 0{,}0136 \approx 1{,}36\,\%

Lies die gegebenen Wahrscheinlichkeiten aus der Aufgabenstellung ab.

$P(A) = 0{,}72\\P(A\cap B)=0{,}18\\P(A \cup B) = 0{,}832$

Verwende den Additionssatz für Wahrscheinlichkeiten.

$\displaystyle P(A\cup B)$	$=$	$\displaystyle P(A) + P(B) - P(A\cap B)$
	↓	Berechne $P(B)$ , indem du den Additionssatz umstellst.
$\displaystyle P(B)$	$=$	$\displaystyle P(A \cup B) - P(A) + P(A\cap B)$
	↓	Setze die Werte ein.
$\displaystyle P(B)$	$=$	$\displaystyle 0{,}832 - 0{,}72 +0{,}18$
$\displaystyle P(B)$	$=$	$\displaystyle 0{,}292$

Berechne $P_B(A)$

$P_B(A) = \dfrac{0{,}18}{0{,}292}\approx 0{,}62$

Berechne die bedingte Wahrscheinlichkeit $P_{\overline{A}}(B)$

Verwende das Gesetz der totalen Wahrscheinlichkeit und stelle nach $P_{\overline{A}}(B)$ um.

$\displaystyle P(B)$	$=$	$\displaystyle P(A)\cdot P_A(B)\;+\;P(\overline A)\cdot P_{\overline A}(B)$	$\displaystyle -P(A)\cdot P_A(B)$
$\displaystyle P(B)-P(A)\cdot P_A(B)$	$=$	$\displaystyle P(\overline{A})\cdot P_{\overline{A}}(B)$	$\displaystyle :P(\overline{A})$
$\displaystyle \frac{P(B)-P(A)\cdot P_A(B)}{P(\overline{A})}$	$=$	$\displaystyle P_{\overline{A}}(B)$
	↓	Seiten vertauscht
$\displaystyle P_{\overline{A}}(B)$	$=$	$\displaystyle \frac{P(B)-P(A)\cdot P_A(B)}{P(\overline{A})}$

Berechne $P(\bar A)$ , die Wahrscheinlichkeit zum Gegenereignis von $A$ .

$P(\bar A) = 1 - P(A) = 1 - 0{,}72 = 0{,}28$

Berechne $P_A(B)$ .

$P_A(B) = \dfrac{P(A\cap B)}{P(A)} = \dfrac{0{,}18}{0{,}72} = 0{,}25$

Berechne $P_{\overline A}(B)$ , indem die Werte in die Gleichung eingesetzt werden.

$P_{\overline A}(B) = \dfrac{0{,}292-0{,}72\cdot 0{,}25}{0{,}28} = 0{,}4$

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

12
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
(Aus dem Leistungskurs-Abitur Bayern 2008/IV) In einem Molkereibetrieb wird Fruchtjoghurt hergestellt und in Becher abgefüllt. In dem Betrieb werden täglich gleich viele Becher der Sorten Erdbeere, Kirsche, Heidelbeere und Ananas abgefüllt. Bei einer Tagesproduktion, bei der 4 % der Becher einen defekten Deckel aufweisen, fällt auf, dass unter den Erdbeerjoghurtbechern sogar jeder zehnte Deckel fehlerhaft ist.
1. Bestimmen Sie den Anteil der Becher mit defektem Deckel unter allen Bechern, die keinen Erdbeerjoghurt enthalten. Klären Sie, ob es durch Absenken des Ausschussanteils allein beim Erdbeerjoghurt gelingen kann, den angestrebten Qualitätsstandard von insgesamt höchstens 1 % Ausschussanteil einzuhalten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bestimme bedingte Wahrscheinlichkeit
  Definiere Ereignisse
  Definiere zunächst die Ereignisse, die in der Aufgabenstellung beschrieben werden.
  Ereignis $A$ : In dem Becher ist Erdbeerjoghurt
  Ereignis $B$ : Der Becher hat einen defekten Deckel
  Definiere Wahrscheinlichkeiten
  Gebe aus der Aufgabenstellung jeweils die Wahrscheinlichkeit an, mit denen eins der zuvor definierten Ereignisse eintritt.
  $P(A) = \frac{1}{4} = 0{,}25$ $P(\overline A) = \frac{3}{4} = 0{,}75$
  In dem Betrieb werden täglich gleich viele Becher der Sorten Erdbeere, Kirsche, Heidelbeere und Ananas abgefüllt.
  $P(B) = 0{,}04$ $P(\overline B) = 0{,}96$
  Bei einer Tagesproduktion, bei der 4 % der Becher einen defekten Deckel aufweisen, …
  $P_A(B) = \frac{1}{10} = 0{,}1$ $P_A(\overline B) = \frac{9}{10} = 0{,}9$
  …, dass unter den Erdbeerjoghurtbechern sogar jeder zehnte Deckel fehlerhaft ist.
  Bestimme den Anteil der Becher mit defektem Deckel unter allen Bechern, die keinen Erdbeerjoghurt enthalten
  Bestimme die bedingte Wahrscheinlichkeit $P_{\overline A} (B)$ . Zeichne dazu ein Baumdiagramm mit den Ereignissen $A$ , $B$ , $\overline A$ und $\overline B$ .
  Schreibe die Wahrscheinlichkeit $P(B)$ als Summe aus $P_{A}(B)$ und $P_{\overline A}(B)$ .
  $P(B) = P_{A}(B) + P_{\overline A}(B)$
  Setze für die Wahrscheinlichkeiten die Werte aus dem Baumdiagramm ein.
  $0{,}04 = \frac{1}{4} \cdot \frac{1}{10} + \frac{3}{4} \cdot x$
  Löse nach $x$ auf.
  $x = 0{,}02$
  Ergebnis
  Der Anteil der Becher mit defektem Deckel unter allen Bechern, die keinen Erdbeerjoghurt enthalten, ist 2 %.
  Kläre, ob es durch Absenken des Ausschussanteils allein beim Erdbeerjoghurt gelingen kann, höchstens 1% Ausschussanteil gesamt zu produzieren
  Es soll insgesamt höchstens 1% Ausschussanteil produziert werden. Es soll also gelten $P(B) \leq 0{,}01$ . Gebe den bestmöglichen Fall an, der durch Absenken des Ausschussanteils allein beim Erdbeerjoghurt erreicht werden kann.
  $P_A (B) = 0$
  Das bestmögliche Ergebnis für die Erdbeerjoghurtbecher ist , wenn alle Erdbeerjoghurtbecher intakte Deckel haben.
  Schreibe die Wahrscheinlichkeit $P(B)$ wieder als Summe aus $P_{A}(B)$ und $P_{\overline A}(B)$ .
  $P(B) = P_{A}(B) + P_{\overline A}(B)$
  Setze die Werte für die Wahrscheinlichkeiten des bestmöglichen Falls mit ausschließlich intakten Erdbeerjoghurtdeckeln ein.
  $P(B) = \frac{1}{4} \cdot 0 + \frac{3}{4} \cdot 0{,}02 = 0{,}015$
  Prüfe, ob $P(B)$ kleiner als 0,01 ist.
  $0{,}015 > 0{,}01$
  Ergebnis
  Es ist nicht möglich, durch Absenken des Ausschussanteils allein beim Erdbeerjoghurt höchstens 1% Ausschussanteil gesamt zu produzieren. Selbst beim Absenken des Ausschussanteils bei Erdbeer auf 0 % hätte insgesamt noch 1,5 % der produzierten Becher einen defekten Deckel.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Alle Becher mit defektem Deckel dieser Tagesproduktion werden aussortiert. Mit welcher Wahrscheinlichkeit enthält ein Becher, der zufällig aus den verbleibenden Bechern ausgewählt wird, Erdbeerjoghurt?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Bestimme bedingte Wahrscheinlichkeit
  Gesucht ist die Wahrscheinlichkeit, dass ein zufällig ausgewählter Becher Erdbeerjoghurt enthält ( $A$ ), wenn bekannt ist, dass dieser Becher einen intakten Deckel ( $\overline B$ ) hat.
  Schreibe als erstes die Definition der bedingten Wahrscheinlichkeit auf.
  Gebe die Wahrscheinlichkeit $P(\overline B)$ an.
  $P(\overline B) = 1 - 0{,}04 = 0{,}96$
  Gebe die Wahrscheinlichkeit $P(A \cap \overline B)$ an.
  Berechne die bedingte Wahrscheinlichkeit.
  Ergebnis
  Die Wahrscheinlichkeit, dass ein zufällig ausgewählter Becher Erdbeerjoghurt enthält ( $A$ ), wenn bekannt ist, dass dieser Becher einen intakten Deckel ( $\overline B$ ) hat, beträgt 23,44 %.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
13
Beim Werfen eines Oktaeders, dessen acht Seitenflächen mit den Ziffern $1$ bis $8$ beschriftet sind, hat Manfred auf das Ereignis $A$ : „Es wird die $1$ oder die $8$ geworfen“ gesetzt.
1. Geben Sie die Wahrscheinlichkeit des Ereignisses $A$ an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit berechnen
  Es gibt $8$ mögliche Zahlen, die gezogen werden können. $2$ davon sind die Gewinnzahlen. Es handelt sich um ein Laplace Experiment. Damit ergibt sich die Wahrscheinlichkeit:
  $P(A)=\frac{2}{8}=\frac{1}{4}=0.25=25\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Manfred kann zunächst nur erkennen, dass die $5$ nicht gewürfelt wurde. Mit welcher Wahrscheinlichkeit kann er daraufhin auf einen Gewinn hoffen?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit berechnen
  Es gibt nur noch $7$ mögliche Zahlen, die gezogen werden können. $2$ davon sind die Gewinnzahlen. Also ergibt sich die Wahrscheinlichkeit als:
  $\frac{2}{7}\approx 29\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Manfred kann zunächst nur erkennen, dass die gewürfelte Augenzahl $6$ oder $8$ ist. Mit welcher Wahrscheinlichkeit kann er daraufhin auf einen Gewinn hoffen?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit berechnen
  Es stehen nur $2$ mögliche Zahlen zur Auswahl, eine davon ist $8$ mit der Manfred gewinnen würde. Also ergibt sich die Wahrscheinlichkeit als:
  $\frac{1}{2}=50\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Geben Sie eine Bedingung $B$ an, sodass $P_B\left(A\right)=P\left(A\right)$ ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit berechnen
  Es gibt viele verschiedenen Lösungsmöglichkeiten. Diese hier ist nur ein Vorschlag.
  Wähle z.B. die Bedingung $B$ = "Die Zahl muss ohne Rest durch $2$ teilbar sein."
  Das sind die Zahlen $2{,}4,6{,}8$ .
  Benutze die Definition der bedingten Wahrscheinlichkeit.
  ↓
  $\displaystyle P_B\left(A\right)$ $=$ $\displaystyle \frac{P\left(A\cap B\right)}{P\left(B\right)}$
  $=$
  $P\left(B\right)=\frac{4}{8}=\frac{1}{2}$ ;
  $P\left(A\cap B\right)=\frac{1}{8}$ ; ( $8$ ist einzige Zahl, die in beiden Ereignissen liegt)
  $=\frac{\displaystyle\frac18}{\displaystyle\frac12}=\frac28=\frac14=25\%$
  Eine sehr simple Antwort wäre auch gewesen, wenn $P(B) = 1$ gewählt werden wäre. z.B. $B$ ="Die Zahl ist eine natürliche Zahl zwischen $1$ und $8$ ."
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
14
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
28 Schülerinnen und 26 Schüler wählen eine Sportart. 14 Buben und Mädchen möchten Schwimmen, zwei Fünftel der übrigen Fußball spielen und der Rest laufen. Beim Fußball sind nur 2 Mädchen, dagegen beim Schwimmen nur 2 Buben.
1. Erstellen Sie eine 6-Felder-Tafel mit absoluten Häufigkeiten.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Sechsfeld-Tafel
  Definiere die Ereignisse, die in der Aufgaben genannt wurden.
  $M$ : Person ist männlich
  $S$ : Person schwimmt
  $F$ : Person spielt Fußball
  $L$ : Person geht Laufen
  Erstelle Sechsfeld-Tafel
  Zeichne eine leere Sechsfeld-Tafel mit Feldern für die Ereignisse $M \cap S$ , $M\cap F$ , $M \cap L$ , $\overline M \cap S$ , $\overline M \cap F$ , $\overline M \cap L$ , $M$ , $\overline M$ , $S$ , $F$ und $L$ , sowie ein Feld für die Gesamtanzahl von Ereignissen.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c|c}\ & \quad \mathrm{S} \quad& \quad\mathrm{F} \quad&\quad \mathrm{L}\quad &\ \\\hline\mathrm{M} & & & & \\\hline\mathrm{\overline M} & & & & \\\hline\ & & & & \end{array}$
  Trage die direkt ersichtlichen Informationen aus der Aufgabenstellung ein.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c|c}\ & \quad \mathrm{S} \quad& \quad\mathrm{F} \quad&\quad \mathrm{L}\quad &\ \\\hline\mathrm{M} & 2 & & & 26\\\hline\mathrm{\overline M} & & 2 & &28 \\\hline\ &14 & & & \end{array}$
  Berechne die Gesamtanzahl der Schüler und Schülerinnen und damit die Anzahl der Fußballer und Läufer.
  $26+28=54$ Gesamtanzahl
  $54-14=40$ Nichtschwimmer
  $\frac{2}{5} \cdot 40=16$ Fußballer
  $40-16=24$ Läufer
  Trage die Werte in die Sechsfeld-Tafel ein.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c|c}\ & \quad \mathrm{S} \quad& \quad\mathrm{F} \quad&\quad \mathrm{L}\quad &\ \\\hline\mathrm{M} & 2 & & & 26\\\hline\mathrm{\overline M} & & 2 & &28 \\\hline\ &14 & 16 & 24 & 54\end{array}$
  Ergänze die fehlenden Felder, indem du von der Anzahl der Ereignisse $S$ die Anzahl der Ereignisse $M \cap S$ abziehst und von der Anzahl der Ereignisse $F$ die Anzahl der Ereignisse $\overline M \cap F$ abziehst.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c|c}\ & \quad \mathrm{S} \quad& \quad\mathrm{F} \quad&\quad \mathrm{L}\quad &\ \\\hline\mathrm{M} & 2 & 14 & & 26\\\hline\mathrm{\overline M} & 12 & 2 & &28 \\\hline\ &14 & 16 & 24 & 54\end{array}$
  Ergänze nun die beiden letzten fehlenden Felder.
  $\def\arraystretch{1.25} \begin{array}{c|c|c|c|c}\ & \quad \mathrm{S} \quad& \quad\mathrm{F} \quad&\quad \mathrm{L}\quad &\ \\\hline\mathrm{M} & 2 & 14 & 10 & 26\\\hline\mathrm{\overline M} & 12 & 2 & 14 &28 \\\hline\ &14 & 16 & 24 & 54\end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Wie groß ist dann die Wahrscheinlichkeit, dass ein Mädchen Fußball spielen möchte? Zeigen Sie, dass das Geschlecht einen Einfluss auf die Fußball-Leidenschaft hat.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: bedingte Wahrscheinlichkeit
  Formuliere die Frage um: "Wie groß ist die Wahrscheinlichkeit, dass eine Person Fußball spielen möchte, wenn bekannt ist, dass diese Person ein Mädchen ist.
  Bestimme die bedingte Wahrscheinlichkeit $P_{\overline M} (F)$ .Schreibe dazu zunächst die Definition der bedingten Wahrscheinlichkeit auf.
  $P_{\overline{M}}(F)=\frac{P(\overline{M}\cap F)}{P(\overline{M})}$
  Lese aus der Sechsfeld-Tafel die Wahrscheinlichkeiten $P(\overline M \cap F)$ und $P(\overline M)$ ab.
  $P(\overline{M}\cap F)=\frac{2}{54}$
  $P(\overline{M})=\frac{28}{54}$
  Berechne nun die bedingte Wahrscheinlichkeit $P_{\overline M} (F)$
  $P_{\overline{M}}(F)=\frac{P(\overline{M}\cap F)}{P(\overline{M})}=\frac{\frac{2}{54}}{\frac{28}{54}}=\frac{2}{28}=0{,}07$
  Ergebnis
  Die Wahrscheinlichkeit, dass ein Mädchen Fußball spielt ist 7,14 %. Offenbar ist die Fußballleidenschaft stark geschlechtsabhängig. Die Wahrscheinlichkeit, dass ein Junge oder Mädchen Fußball spielt ist vergleichsweise 29,6 %.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Wie groß ist die Wahrscheinlichkeit, dass jemand aus der Fußball-Gruppe aus der Gruppe der Mädchen stammt?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: bedingte Wahrscheinlichkeit
  Formuliere die Frage um: "Wie groß ist die Wahrscheinlichkeit, dass eine Person ein Mädchen ist, wenn bekannt ist, dass diese Person Fußball spielt.
  Bestimme die bedingte Wahrscheinlichkeit $P_{F} (\overline M)$ . Schreibe dazu zunächst die Definition der bedingten Wahrscheinlichkeit auf.
  $P_F(\overline{M})=\frac{P(\overline{M}\cap F)}{P(F)}$
  Lese aus der Sechsfeld-Tafel die Wahrscheinlichkeiten $P(\overline M \cap F)$ und $P(F)$ ab.
  $P(\overline{M}\cap F)=\frac{2}{54}$
  $P(F)=\frac{16}{54}$
  Berechne nun die bedingte Wahrscheinlichkeit $P_{F} (\overline M)$
  $P_F(\overline{M})=\frac{P(\overline{M}\cap F)}{P(F)}=\frac{\frac{2}{54}}{\frac{16}{54}}=\frac{2}{16}=0{,}125$
  Ergebnis
  Die Wahrscheinlichkeit, dass es sich bei einer Person, die Fußball spielt, um ein Mädchen handelt, ist 12,5 %.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Gegeben ist ein Beutel mit x Laplace-Münzen, wobei eine auf beiden Seiten Wappen trägt und die anderen jeweils auf einer Seite Wappen und auf der anderen Seite Zahl.

Es wird eine Münze aus dem Beutel gezogen und diese zweimal hintereinander geworfen. Die Wahrscheinlichkeit, dass zweimal Wappen erscheint, liegt bei $\frac{1}{2}$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \frac{1}{x}+\frac{x-1}{4x}$	$=$	$\displaystyle \frac{1}{2}$
	↓	Auf den Hauptnenner $4x$ erweitert.
$\displaystyle \frac{4}{4x}+\frac{x-1}{4x}$	$=$	$\displaystyle \frac{2x}{4x}$	$\displaystyle \cdot4x$
$\displaystyle 4+(x-1)$	$=$	$\displaystyle 2x$
$\displaystyle x+3$	$=$	$\displaystyle 2x$	$\displaystyle -x$
$\displaystyle 3$	$=$	$\displaystyle x$
$\displaystyle x$	$=$	$\displaystyle 3$

$\displaystyle \text{P(ww) } \cdot x - 1$	$=$	$\displaystyle 0$	$\displaystyle \text{Term für P(ww) einsetzen}$
$\displaystyle \left( \frac{1}{5} \cdot 1 - \frac{4}{5} \cdot \frac{1}{4}\right) \cdot x - 1$	$=$	$\displaystyle 0$	$\displaystyle \text{Klammer zusammenfassen}$
$\displaystyle \frac{2}{5} \cdot x - 1$	$=$	$\displaystyle 0$	$\displaystyle +1$
$\displaystyle \frac{2}{5} \cdot x$	$=$	$\displaystyle 1$	$\displaystyle \cdot \frac{5}{2}$
$\displaystyle x$	$=$	$\displaystyle \frac{5}{2} = 2{,}50$

$\displaystyle \frac{\frac{1}{5} \cdot 1^x}{\frac{1}{5} \cdot 1^x + \frac{4}{5} \cdot \left( \frac{1}{2}\right)^x}$	$≥$	$\displaystyle \frac{95}{100}$	$\displaystyle \text{Vereinfachen } 1^x = 1$
$\displaystyle \frac{\frac{1}{5}}{\frac{1}{5} + \frac{4}{5} \cdot \left( \frac{1}{2}\right)^x}$	$≥$	$\displaystyle \frac{95}{100}$	$\displaystyle \text{mit 5 erweitern ; } \left( \frac{1}{2}\right)^x = 2^{-x}$
$\displaystyle \frac{1}{1 + 4 \cdot 2^{-x}}$	$≥$	$\displaystyle \frac{95}{100}$	$\displaystyle \cdot (1 + 4 \cdot 2^{-x}) \cdot 100$
$\displaystyle 100$	$≥$	$\displaystyle 95 \cdot (1 + 4 \cdot 2^{-x})$	$\displaystyle \text{Klammer ausmultiplizieren}$
$\displaystyle 100$	$≥$	$\displaystyle 95 + 380 \cdot 2^{-x}$	$\displaystyle - 95$
$\displaystyle 5$	$≥$	$\displaystyle 380 \cdot 2^{-x}$	$\displaystyle :5 \cdot 2^x$
$\displaystyle 2^x$	$≥$	$\displaystyle 76$	$\displaystyle \log_2()$
$\displaystyle x$	$≥$	$\displaystyle 7$

Benutze die Definition der bedingten Wahrscheinlichkeit.
	↓
$\displaystyle P_B\left(A\right)$	$=$	$\displaystyle \frac{P\left(A\cap B\right)}{P\left(B\right)}$
	$=$

Aufgaben zum Thema bedingte Wahrscheinlichkeit

Ereignisse definieren

Definition der bedingten Wahrscheinlichkeit angeben

Benötigte Wahrscheinlichkeiten herausfinden

Definiere Ereignisse

Definiere Wahrscheinlichkeiten

Berechne bedingte Wahrscheinlichkeit

Ergebnis

Ergänzung

Hast du eine Frage oder Feedback?

Definiere Ereignisse

Definiere Wahrscheinlichkeiten

Berechne bedingte Wahrscheinlichkeit

Ergebnis

Hast du eine Frage oder Feedback?

Definiere Ereignisse

Berechne Wahrscheinlichkeiten

Ergebnis

Hast du eine Frage oder Feedback?

Erstellen der Vierfeldertafel:

Erstellen des 1. Baumdiagramms:

Erstellen des 2. Baumdiagramms:

Hast du eine Frage oder Feedback?

Alternativlösung

Hast du eine Frage oder Feedback?

Alternativlösung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Ergebnis

Hast du eine Frage oder Feedback?

Ergebnis

Hast du eine Frage oder Feedback?

Ergebnis

Hast du eine Frage oder Feedback?

Die Ereignisse

Gegebenen bedingten Wahrscheinlichkeiten

Berechnung der gesuchten Wahrscheinlichkeit

Hast du eine Frage oder Feedback?

Ergebnis

Hast du eine Frage oder Feedback?

Ergebnis

Hast du eine Frage oder Feedback?

Berechne relative Häufigkeiten

Auflistung der Wahrscheinlichkeiten in der Tabelle

Ergebnis

Hast du eine Frage oder Feedback?

Berechne alle Pfadwahrscheinlichkeiten

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gegenwahrscheinlichkeit

Vierfeldertafel

Hast du eine Frage oder Feedback?

Ergebnis

Hast du eine Frage oder Feedback?

Berechne Wahrscheinlichkeiten

Hast du eine Frage oder Feedback?

Berechne alle Pfadwahrscheinlichkeiten

Hast du eine Frage oder Feedback?

Ergebnis

Hast du eine Frage oder Feedback?

Ergebnis

Hast du eine Frage oder Feedback?

Ergebnis

Hast du eine Frage oder Feedback?

Berechne absolute Häufigkeiten

Hast du eine Frage oder Feedback?

Ermittle Wahrscheinlichkeiten

Zeichne das Baumdiagramm

Hast du eine Frage oder Feedback?

Ermittle Wahrscheinlichkeiten

Zeichne das Baumdiagramm

Hast du eine Frage oder Feedback?

Teilaufgabe 1

Teilaufgabe 2

Teilaufgabe 3

Teilaufgabe 4

Hast du eine Frage oder Feedback?

Berechne die bedingte Wahrscheinlichkeit PB(A)P_B(A)PB​(A)

Berechne die bedingte Wahrscheinlichkeit PA‾(B)P_{\overline{A}}(B)PA​(B)

Bestimme den Anteil der Becher mit defektem Deckel unter allen Bechern, die keinen Erdbeerjoghurt enthalten

Berechne die bedingte Wahrscheinlichkeit $P_B(A)$

Berechne die bedingte Wahrscheinlichkeit $P_{\overline{A}}(B)$