Mächtigkeit

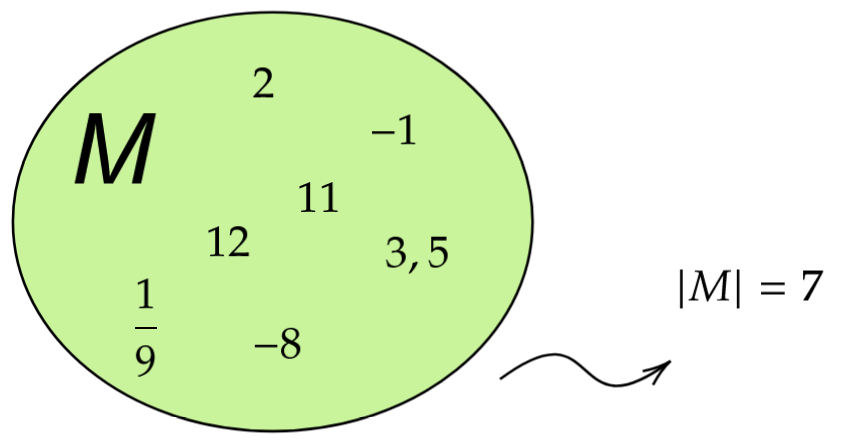
Grundlagen zur Mächtigkeit

Gleichmächtig

Die Menge $A=\{\mathrm{2,3,5,7}\}$ aller einstelligen Primzahlen besitzt $4$ Elemente. Es ist damit:

Die Menge $B=\left\{\mathrm{2,4,6,8}\right\}$ besitzt ebenso $\left|B\right|=4$ Elemente. Wenn zwei Mengen, so wie $A$ und $B$ gleich viele Elemente besitzen, also $\left|A\right|=\left|B\right|$ gilt, nennt man die Mengen gleichmächtig.

Unendlich große Mengen

Falls $M$ unendlich viele Elemente hat, ist die Mächtigkeit unendlich ($\infty$). So ist die Mächtigkeit der Menge der natürlichen Zahlen $\mathbb{N}$ unendlich und wir schreiben $|\mathbb{N}|=\infty$.

Beispiele

• $|A|=\left|\{\mathrm{Baum},\mathrm{Busch},\mathrm{Blatt}\}\right|=3$

• $|B|=\left|\left\{\mathrm{1,2,100,30}\right\}\right|=4$

• $|C|=\left|\left\{\mathrm{1,1,1,1,2}\right\}\right|=2$, da eine Menge ein Element nicht mehrmals enthalten kann!

• $|D|=|A\cup B|=|\{\mathrm{Baum},\mathrm{Busch},\mathrm{Blatt},\mathrm{1,2,100,30}\}|=3+4-0=7$

Mächtigkeit in der Wahrscheinlichkeit

Der Begriff der Mächtigkeit einer Menge wird unter anderem in der Stochastik verwendet. Dort fasst man alle möglichen Ergebnisse eines Zufallsexperiments in die Menge „Ergebnisraum“ $\mathrm{\Omega }$ zusammen. Die Mächtigkeit des Ergebnisraums $|\mathrm{\Omega }|$ ist damit die Anzahl aller möglichen Ergebnisse eines Zufallsexperiments.

Laplace-Wahrscheinlichkeit

Die Wahrscheinlichkeit im Laplace-Experiment ist gegeben durch die Mächtigkeiten der Ereignis- und Ergebnismenge.

Das Ereignis $A=\left\{\mathrm{1,5}\right\}$ beim Würfeln mit einem Würfel besitzt die Wahrscheinlichkeit:

Rechenregeln

• $|M\cup N|=\left|M\right|+\left|N\right|-|M\cap N|$. Vergleiche dazu: Mengenlehre.

• $|M\times N|=\left|M\right|\cdot \left|N\right|$. Vergleiche dazu: kartesisches Produkt.

Potenzmenge

Die Mächtigkeit der Potenzmenge einer Menge $A$, ist: $𝒫(A)=2^{\left|A\right|}$. Ein Beispiel für eine Potenzmenge ist der Ereignisraum.