Aufgaben zum Lösen von Sachaufgaben mit x-Ansatz
Mit diesen gemischten Aufgaben lernst du, gesuchte Größen mithilfe von zu berechnen.
- 1
Auf dem nebenstehenden Bild siehst du eine Rasenfläche, auf der ein Spielfeld als Rechteck der Länge 90 Meter und der Breite 45 Meter mit weißer Farbe markiert werden soll. Dafür möchte der Sportverein "Serlo 2009" Farbe für das Markieren der Linien kaufen.

Stelle einen Term für den Umfang des weißen Rechtecks auf und berechne diesen.
m UmfangWie viele Eimer Farbe muss der Sportverein mindestens kaufen, wenn man mit einem Eimer 30 Meter Linien markieren kann?
Eimer Farbe
- 2
Alex hat eine ungewöhnliche Abmachung mit seinen Eltern: Er erhält für jede Drei im Zeugnis einen bestimmten Geldbetrag von seinen Eltern, für eine Zwei bekommt er das Doppelte und für eine Eins sogar das Dreifache dieses Betrages. Für eine Vier bekommt er nichts, während für eine Fünf das Doppelte des Betrages für eine Zwei abgezogen werden und für eine Sechs das Vierfache des Betrages für eine Eins abgezogen werden. Im Zwischenzeugnis hat Alex folgende Noten: 1 mal Eins, 1 mal Zwei, 4 mal Drei, 2 mal Vier, 1 mal Fünf und 1 mal Sechs. Nachdem Alex in diesem Halbjahr so wenig erfolgreich war, werden ihm 42€ vom Taschengeld abgezogen. Berechne mit Hilfe eines x-Ansatzes, wieviel für jede Note berechnet wird.
- 3
In einem Verein mit 25 Mitgliedern haben 12 Mitglieder jeweils 2000€ eingezahlt. 12 weitere Mitglieder haben jeweils 1500€ beigesteuert. Auf dem Vereinskonto befinden sich 17000€. Wie ist das zu erklären? Führe eine Rechnung mit einem x-Ansatz durch!
- 4
Berechne jeweils die Winkel.
In einem rechtwinkligen Dreieck ist der eine Winkel an der Hypotenuse um 32° kleiner als der andere. Berechne den gesuchten Winkel.
GradIn einem rechtwinkligen Dreieck ist einer der beiden spitzen Winkel halb so groß wie der andere.
In einem Dreieck ist um 20° kleiner als und doppelt so groß wie .
- 5
Marco, Sabine, Volker und Lena haben zusammen 66€. Marco hat 2€ weniger als Sabine, Volker hat doppelt so viel wie Sabine und Lena doppelt so viel wie Marco. Berechne wie viel Geld Marco, Sabine, Volker und Lena haben.
Löse mit Hilfe eines Gesamtansatzes.
- 6
Berechne x am Rechteck ABCD. (Die Zeichnung ist nicht maßstabgerecht.)
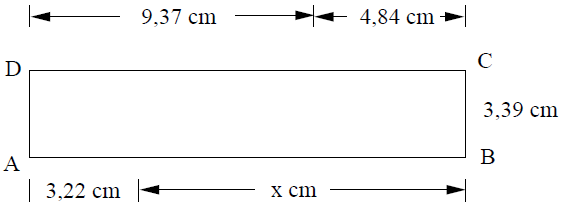 cm
cm - 7
Verlängert man zwei gegenüberliegende Seiten eines Quadrats um jeweils 3 cm und verkürzt die anderen Seiten um jeweils 2 cm, so entsteht ein Rechteck, dessen Flächeninhalt um größer ist als der des Quadrats. Wie lang sind die Seiten des Quadrats?
cm - 8
Aus einem Draht von einem Meter Länge wurde das Kantenmodell eines Würfels gebaut. Es blieb ein Reststück von 4,0 cm. Wie lang ist eine Würfelkante?
cm - 9
Ein Vater, seine Tochter und sein Sohn sind zusammen genauso alt wie ihre 77-jährige Oma. Der Vater ist doppelt so alt wie seine Tochter welche 3 Jahre älter ist als der Sohn. Berechne das Alter des Vaters, der Tochter und des Sohnes mithilfe einer Gleichung.
- 10
Zahlenrätsel
Löse die folgenden Aufgaben durch Aufstellen einer geeigneten Gleichung.
Die Summe von zwei Zahlen ist , ihre Differenz ist .
Drei aufeinander folgende Zahlen ergeben zusammen addiert .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
