Es gibt drei binomische Formeln,
die erste (Plus-Formel),
die zweite (Minus-Formel) und
die dritte (Plus-Minus-Formel)
Alle drei kommen oft vor und sind wichtige Hilfsmittel zum Rechnen.
1. binomische Formel
Beispiel:
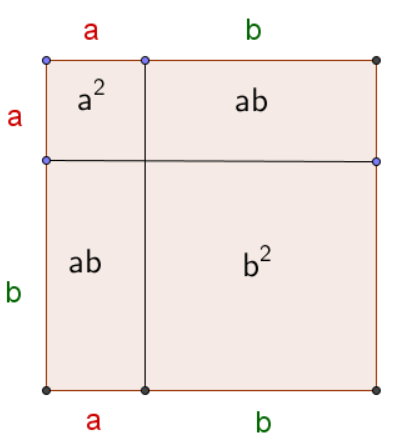
2. binomische Formel
Beispiel:

3. binomische Formel
Beispiel:
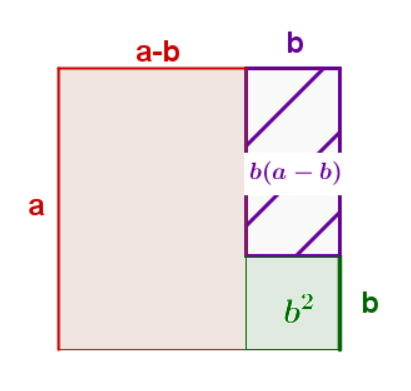
Verwendung der binomischen Formeln
Die binomischen Formeln werden in zwei verschiedene Richtungen angewendet:
"vorwärts" zum Auflösen der Klammern oder
"rückwärts" zum Umwandeln einer Summe bzw. Differenz in ein Produkt ("Faktorisieren")
Binomische Formeln "vorwärts" (d.h. zum Auflösen der Klammern)
Hierbei wird ein Produktterm in eine Summe oder Differenz umgewandelt.
Allgemeine Vorgehensweise
Terme vergleichen und entscheiden, welche Formel man anwenden muss
Sich klarmachen, was und ist
Formel anwenden
Beispiele
1. binomische Formel:
2. binomische Formel:
3. binomische Formel:
Binomische Formeln "rückwärts" (d.h. zum Faktorisieren)
Man kann die binomische Formel auch umgekehrt anwenden. Hier macht man aus Summen Produkte. Das hat vor allem Vorteile beim Kürzen.
Allgemeine Vorgehensweise
Zuerst musst du überprüfen, wie viele Summanden der Term besitzt.
Sind es drei, so kommen die ersten beiden Formeln infrage,
sind es zwei, so kann die dritte Formel hilfreich sein,
sind es mehr als drei Summanden, so muss man zuerst versuchen, die Terme zusammenfassen.
Drei Summanden
Hat man drei Summanden, so überprüft man, ob zwei der Summanden Quadrate mit positiven Vorzeichen sind. Notfalls muss man zuerst einen geeigneten Faktor ausklammern. Die Wurzeln dieser Quadrate nennt man und .
Ist dies der Fall, so muss man noch den mittleren Term überprüfen, indem man berechnet.
Falls dieses Ergebnis mit dem mittleren Summanden aus der Aufgabenstellung übereinstimmt, kann man die binomische Formel zum Faktorisieren benutzen, indem man nun noch das Vorzeichen betrachtet und je nachdem die erste oder die zweite binomische Formel benutzt.
Zwei Summanden
Hat man zwei Summanden, so überprüft man, ob nur vor einem der beiden Summanden ein Minuszeichen steht.
Ist dies der Fall, so überprüft man, ob die beiden Summanden Quadrate sind. Ist das auch der Fall, so kann man mithilfe der dritten binomischen Formel faktorisieren.
Falls keiner der Summanden ein Quadratterm ist, kann man noch versuchen, einen geeigneten Faktor auszuklammern.
Keiner der Wege funktioniert
Der Term lässt sich nicht mithilfe einer binomischen Formel faktorisieren. Hier kannst du nur vereinfachen, indem du die quadratische Ergänzung benutzt, das ist dann allerdings keine Faktorisierung mehr.
Der zugehörige Entscheidungsbaum sieht aus wie folgt:
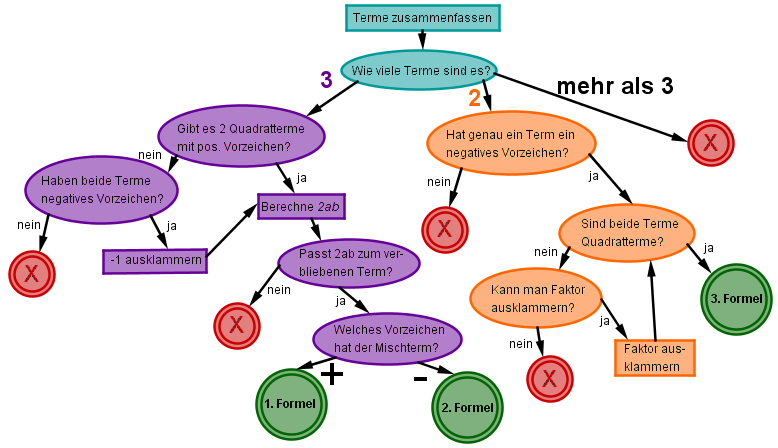
Beispiel 1
Man kann nichts ausklammern/zusammenfassen und wir haben drei Summanden.
Es gibt 2 Quadratterme: und
Sie haben beide ein positives Vorzeichen.
Mischterm überprüfen:
, , also muss der Mischterm sein.
Das passt zur 1. binomischen Formel mit und .
Man bekommt das Ergebnis .
Beispiel 2
Den Term ausklammern:
Es gibt 2 Quadratterme: und
hat positives Vorzeichen, hat negatives Vorzeichen.
Es lässt sich die 3. binomische Formel anwenden, mit und .
Man bekommt als Ergebnis .
Beispiel 3
Den Term ausklammern:
Es gibt 2 Quadratterme: und
Sie haben beide positives Vorzeichen.
Mischterm überprüfen:
, , also muss der Mischterm sein.
Die Mischterme stimmen nicht überein.
Es lässt sich keine binomische Formel anwenden.
Video zum Thema Binomische Formeln
Laden
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu den binomischen Formeln
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
