Die Division ist eine der vier Grundrechenarten. Als Zeichen für die Division wird meist der Doppelpunkt verwendet.

Durch die Division wird ausgerechnet, wie oft in der Zahl, die vor dem Divisionszeichen steht, die Zahl enthalten ist, die hinter dem Divisionszeichen steht.
Die Division ist damit die Umkehroperation zur Multiplikation.
Beispiel für eine Division
Ein Beispiel für eine Divisionsaufgabe ist:
Dies spricht man " dividiert durch " oder auch " geteilt durch ".
Teilt man nun durch , überlegt man, wie oft die in die "hineinpasst".
Das Ergebnis ist , weil ist,
das heißt, weil ist.
Sind die Zahlen zu groß dafür, dass man sich im Kopf überlegt, wie oft die zweite Zahl in die erste passt, kann man die schriftliche Division verwenden.
Wichtige Bezeichnungen einer Division
Für die einzelnen "Bestandteile" einer Division sind bestimmte Begriffe festgelegt:
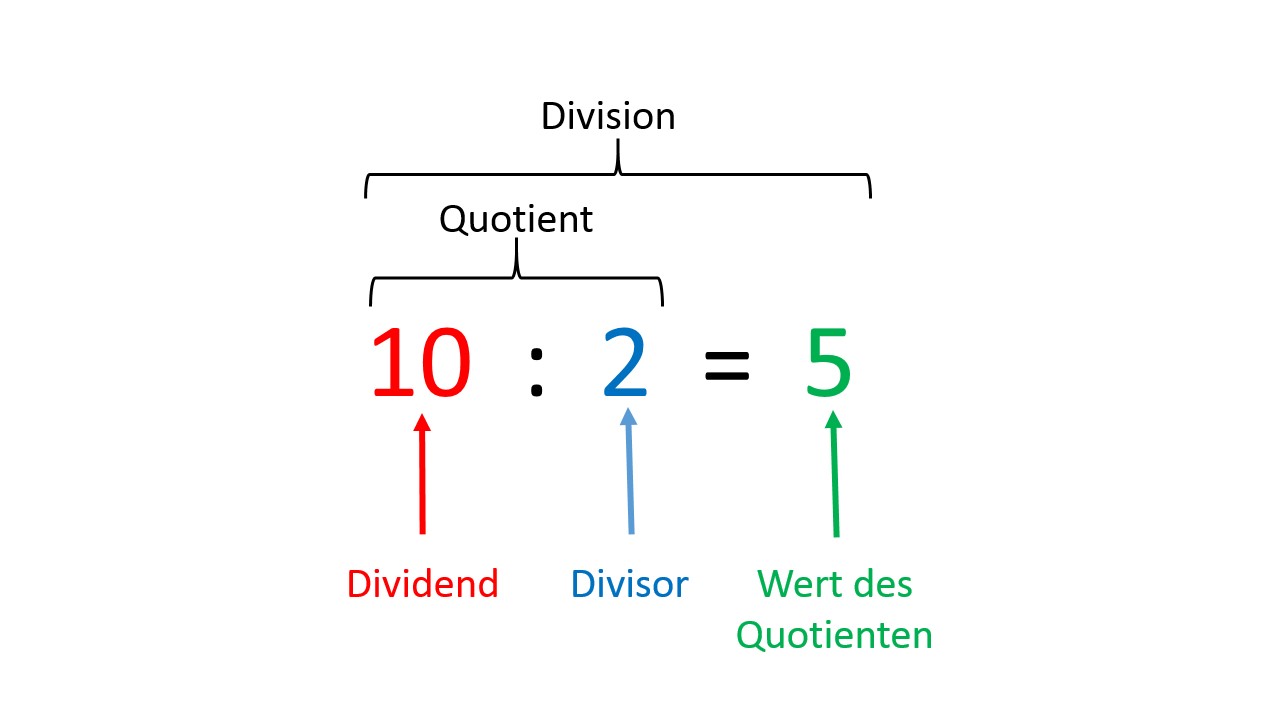
Die Division setzt sich aus verschiedenen Begriffen zusammen. Teilt man so zum Beispiel die Zahl durch , heißt Dividend und Divisor. Den Rechenterm nennt man Quotient. Das Ergebnis der Rechnung nennt man Wert des Quotienten.
Dividieren lernen am Beispiel
| ↓ | Man fragt sich: "Wie oft passt der Divisor (2) in den Dividenden (10)?" | ||
| ↓ | Kontrolle | ||
Teiler des Dividenden

Wenn sowohl der Dividend, der Divisor als auch der Wert des Quotienten eine ganze Zahl ist, nennt man den Divisor einen Teiler des Dividenden.
Beispiele für Teiler der Zahl 6
Die Teiler der Zahl sind: , denn:
Die Zahl hingegen ist zum Beispiel kein Teiler von 6, da bei der Rechnung Rest nicht ohne Rest eine ganze Zahl rauskommt.
Besondere Divisionen
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Division
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
