Aufgaben zur Prozentdarstellung
Lerne mit diesen Aufgaben die Darstellung mit der Prozentschreibweise. Schaffst du sie alle?
- 1
Gib die gefärbte Fläche in Prozent-, Dezimal- und Bruchschreibweise an.
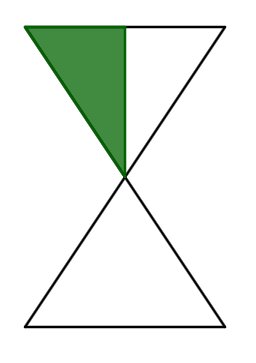
Für diese Aufgabe benötigst Du folgendes Grundwissen: Fläche zusammengesetzter Figuren
Veranschaulichung der drei Zahldarstellungen
Der gefärbte Anteil beträgt:
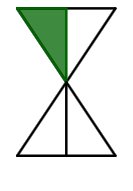
Die Sanduhr kannst du in vier gleich große rechtwinklige Dreicke aufteilen. Eines davon ist grün eingefärbt. Das heißt, ein Teil von insgesamt vier ist farbig.
Hast du eine Frage oder Feedback?
Überlege dir, wie du die Sanduhr in gleich große Flächen unterteilen kannst.
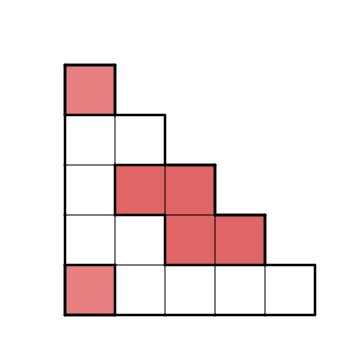
Für diese Aufgabe benötigst Du folgendes Grundwissen: Fläche zusammengesetzter Figuren
Veranschaulichung der drei Zahldarstellungen
Der gefärbte Anteil beträgt:
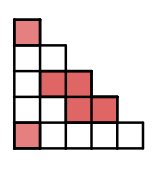
Die Treppe kannst du in 15 gleich große Quadrate aufteilen. Sechs davon sind rot eingefärbt. Das heißt, sechs Teile von insgesamt 15 sind farbig.
Hast du eine Frage oder Feedback?
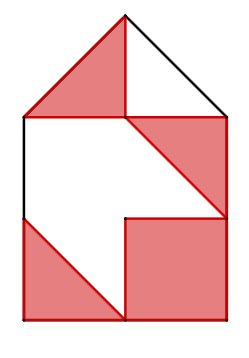
Für diese Aufgabe benötigst Du folgendes Grundwissen: Fläche zusammengesetzter Figuren
Veranschaulichung der drei Zahldarstellungen
Der gefärbte Anteil beträgt:
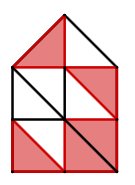
Das Haus kannst du in zehn gleich große rechtwinklige Dreiecke aufteilen. Fünf davon sind rot eingefärbt. Das heißt, fünf Teile von insgesamt zehn sind farbig.
Hast du eine Frage oder Feedback?
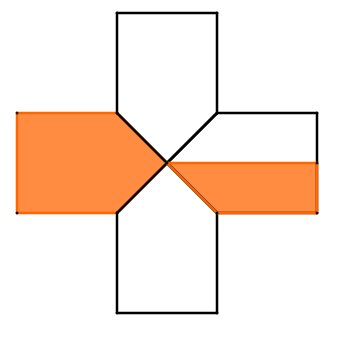
Für diese Aufgabe benötigst Du folgendes Grundwissen: Fläche zusammengesetzter Figuren
Veranschaulichung der drei Zahldarstellungen
Der gefärbte Anteil beträgt:
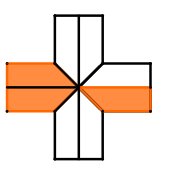
Das Kreuz kannst du in acht gleich große Trapeze aufteilen. Drei davon sind orange eingefärbt. Das heißt, drei Teile von insgesamt acht sind farbig.
Hast du eine Frage oder Feedback?
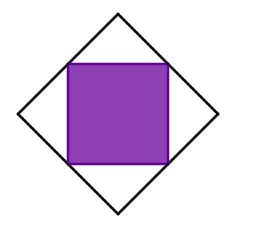
Für diese Aufgabe benötigst Du folgendes Grundwissen: Fläche zusammengesetzter Figuren
Veranschaulichung der drei Zahldarstellungen
Der gefärbte Anteil beträgt:

Die Raute kannst du in acht gleich große gleichschenklige Dreiecke aufteilen. Vier davon sind lila eingefärbt. Das heißt, vier Teile von insgesamt acht sind farbig.
Hast du eine Frage oder Feedback?
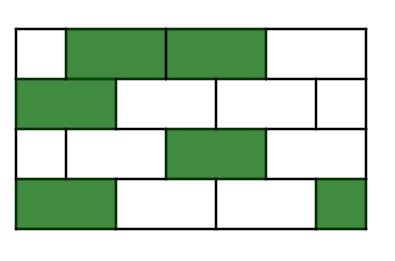
Für diese Aufgabe benötigst Du folgendes Grundwissen: Fläche zusammengesetzter Figuren
Veranschaulichung der drei Zahldarstellungen
Der gefärbte Anteil beträgt:

Die Mauer kannst du in 28 gleich große Quadrate aufteilen. Elf davon sind grün eingefärbt. Das heißt, elf Teile von insgesamt 28 sind farbig.
Hast du eine Frage oder Feedback?
- 2
Peter ist sein Smartphone runtergefallen. Er sagt, dass in den oberen 70 % seines Handys nur noch schwarz anzeigt wird. Zeichne in das folgende Bild ein, wie Peters Smartphone nun aussehen könnte.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Bruchzahl und Prozentzahl
Beachte zuerst, dass das Display in 10 Teile geteilt ist. Willst du des Displays auswählen, also , so musst du diesen Bruch zunächst auf die 10 Teile übertragen, indem du kürzt:
Wählst du 7 der 10 Teile aus, so bekommst du den Anteil .
Beachte außerdem, dass der Schaden im oberen Displayteil ist und du deswegen mit der Auswahl von oben nach unten starten solltest.
Eine mögliche Lösung siehst du hier:
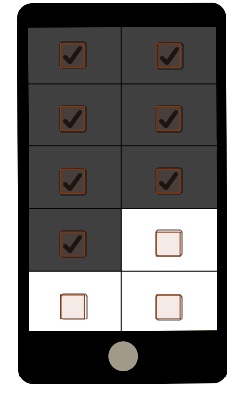
- 3
Wandle um! Dezimalzahldarstellung Prozentzahldarstellung
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Dezimalzahlen in Prozentangaben
Du multiplizierst die Dezimalzahl mit 100 beziehungsweise verschiebst das Komma um zwei Stellen nach rechts.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Dezimalzahlen in Prozentangaben
Du multiplizierst die Dezimalzahl mit 100 beziehungsweise verschiebst das Komma um zwei Stellen nach rechts.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Dezimalzahlen in Prozentangaben
Du multiplizierst die Dezimalzahl mit 100 beziehungsweise verschiebst das Komma um zwei Stellen nach rechts.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Dezimalzahlen in Prozentangaben
Du multiplizierst die Dezimalzahl mit 100 beziehungsweise verschiebst das Komma um zwei Stellen nach rechts.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Dezimalzahlen in Prozentangaben
Du multiplizierst die Dezimalzahl mit 100 beziehungsweise verschiebst das Komma um zwei Stellen nach rechts.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Dezimalzahlen in Prozentangaben
Du dividierst die Prozentzahl durch 100 beziehungsweise verschiebst das Komma um zwei Stellen nach links.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Dezimalzahlen in Prozentangaben
Du dividierst die Prozentzahl durch 100 beziehungsweise verschiebst das Komma um zwei Stellen nach links.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Dezimalzahlen in Prozentangaben
Du dividierst die Prozentzahl durch 100 beziehungsweise verschiebst das Komma um zwei Stellen nach links.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Dezimalzahlen in Prozentangaben
Du dividierst die Prozentzahl durch 100 beziehungsweise verschiebst das Komma um zwei Stellen nach links.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Dezimalzahlen in Prozentangaben
Du dividierst die Prozentzahl durch 100 beziehungsweise verschiebst das Komma um zwei Stellen nach links.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Dezimalzahlen in Prozentangaben
Du dividierst die Prozentzahl durch 100 beziehungsweise verschiebst das Komma um zwei Stellen nach links.
Hast du eine Frage oder Feedback?
- 4
Wandle um!
Bruchzahldarstellung in Prozentzahldarstellung bzw.
Prozentdarstellung in Bruchzahldarstellung. Kürze hier soweit wie möglich!
- %
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Bruchzahlen in Prozentangaben
Du erweiterst mit 25 auf Hundertstel. Da sind gleich .
Hast du eine Frage oder Feedback?
- %
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Bruchzahlen in Prozentangaben
Du erweiterst mit 10 auf Hundertstel. Da sind gleich .
Hast du eine Frage oder Feedback?
- %
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Bruchzahlen in Prozentangaben
Du erweiterst mit auf Hundertstel. Da sind gleich .
Hast du eine Frage oder Feedback?
- %
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Bruchzahlen in Prozentangaben
Du erweiterst mit auf Hundertstel. Da sind gleich .
Hast du eine Frage oder Feedback?
- %
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Bruchzahlen in Prozentangaben
Du erweiterst mit auf Hundertstel. Da sind gleich .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Prozentangaben in Bruchzahlen
Da Prozent Hundertstel bedeutet, sind gleich . Kürze nun diesen Bruch so weit wie möglich. In diesem Fall lassen sich zwei mal mit kürzen.
Hast du eine Frage oder Feedback?
19%
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Prozentangaben in Bruchzahlen
Da Prozent Hundertstel bedeutet, sind gleich . Kürze nun diesen Bruch so weit wie möglich. In diesem Fall lassen sich nicht kürzen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Prozentangaben in Bruchzahlen
Da Prozent Hundertstel bedeutet, sind gleich . Kürze nun diesen Bruch so weit wie möglich. In diesem Fall lassen sich mit kürzen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Prozentangaben in Bruchzahlen
Da Prozent Hundertstel bedeutet, sind gleich . Kürze nun diesen Bruch so weit wie möglich. In diesem Fall lassen sich zwei mal mit kürzen.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Prozentangaben in Bruchzahlen
Da Prozent Hundertstel bedeutet, sind gleich . Kürze nun diesen Bruch so weit wie möglich. In diesem Fall lassen sich mit kürzen.
Hast du eine Frage oder Feedback?
- 5
Wandle folgende Prozentangaben in Hundertsteldarstellung um!
24%
Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozent
Verwende die Formel
24% =
24% = 0,24
Hast du eine Frage oder Feedback?
99%
Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozent
Verwende die Formel
99% = 0,99
Hast du eine Frage oder Feedback?
3%
Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozent
Verwende die Formel
3% = 0,03
Hast du eine Frage oder Feedback?
80%
Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozent
Verwende die Formel
80% = 0,80
Hast du eine Frage oder Feedback?
- 6
Ordne die folgenden Zahlen der Größe nach! Verwende "<".
- 7
Gib in Prozent an!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Bruchzahlen in Prozentangaben
Da sich nicht in Hundertstel umrechnen lässt, musst du die Bruchzahl erst in eine Dezimalzahl umwandeln und anschließend in eine Prozentzahl.
= =
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Bruchzahlen in Prozentangaben
=
Da sich nicht in Hundertstel umrechnen lässt, musst du die Bruchzahl erst in eine Dezimalzahl umwandeln und anschließend in eine Prozentzahl.
= =
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Bruchzahlen in Prozentangaben
Da sich nicht in Hundertstel umrechnen lässt, musst du die Bruchzahl erst in eine Dezimalzahl umwandeln und anschließend in eine Prozentzahl.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Bruchzahlen in Prozentangaben
=
Da sich nicht in Hundertstel umrechnen lässt, musst du die Bruchzahl erst in eine Dezimalzahl umwandeln und anschließend in eine Prozentzahl.
= =
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Umwandeln von Bruchzahlen in Prozentangaben
=
Da sich nicht in Hundertstel umrechnen lässt, musst du die Bruchzahl erst in eine Dezimalzahl umwandeln und anschließend in eine Prozentzahl.
= =
Hast du eine Frage oder Feedback?
- 8
Auf diesem Zahlenstrahl sind fünf Zahlen eingezeichnet. Lies sie ab und schreibe sie anschließend in Prozentzahldarstellung!

Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentzahl
A: 0,2 = 20%
B: 0,5 = 50%
C: 0,85 = 85%
D: 1,1 = 110%
E: 1,35 = 135%
Jeder Strich bedeutet einen 0,05er Schritt auf dem Zahlenstrahl. Lies die Dezimalzahlen durch Abzählen der Striche ab. Durch Multiplikation mit 100 oder Kommaverschiebung um zwei Stellen nach rechts erhältst du die Prozentzahl.
- 9
Zeichne einen Zahlenstrahl mit den Werten von bis . Markiere darin die folgenden fünf Punkte.
A:
B:
C:
D:
E:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Zahlenstrahl
Tipp: Einen ähnlichen Zahlenstrahl findest du in dieser Aufgabe.
Lösung:

- 10
Nimm ein DIN A4-Blatt und falte es dreimal hintereinander jeweils genau in der Mitte. Vergleiche es mit einem anderen, ungefalteten DIN A4-Blatt. Wie viel Prozent der Fläche des ungefalteten Blattes hat das gefaltete? Schreibe dir zur Hilfestellung auch schon beim ersten und zweiten Mal Falten den Prozentvergleich mit dem ursprünglichen Blatt auf.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozentbestimmung eines Achtelblattes
Mit jedem Falten durch die Mitte halbiert sich die Fläche des Blattes. Damit halbiert sich jedes mal auch die Prozentzahl, die der Fläche entspricht.
Du beginnst mit 100%, die dem ganzen Blatt entsprechen.
Ein ganzes Blatt entspricht 100%
Bisher hast du noch nicht gefaltet und da sich deshalb noch nichts an der Fläche geändert hat, hast du noch 100% der Fläche. Mit dem ersten Mal Falten halbiert sich die Fläche und genauso auch die ihr entsprechende Prozentzahl.
Ein halbes Blatt entspricht 50%
Das halbe Blatt wird ebenso halbiert und zu einem Viertelblatt. Wieder halbieren sich dabei auch die entsprechenden 50% zu 25%.
Ein Viertelblatt entspricht 25%
Wenn du das Viertelblatt halbierst, bekommst du ein Achtelblatt und ebenso halbierst du 25% zu 12,5%.
Ein Achtelblatt entspricht 12,5%
Damit hast du das Ergebnis erhalten.
Nach drei Mal Falten hast du also noch 12,5% der ursprünglichen Fläche des Papiers.
Mache dir klar, dass das gefaltete Blatt acht Mal in das ungefaltete passt, genauso wie 12,5 acht Mal in 100 passt.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
