1 Übersicht
Ziele des Kurses
Dieser Kurs soll einen Überblick zu Vektoren liefern. Zunächst wird geklärt, was ein Vektor ist. Anschließend werden Schritt für Schritt die wichtigsten mathematischen Operationen mit Vektoren erklärt und mit zahlreichen Beispielaufgaben vertieft.
Voraussetzungen
Um Unklarheiten zu vermeiden, sollte man sich bereits mit folgenden Themen gut auskennen:
Grundrechenarten
Grundlagen der Geometrie
2D- und 3D-Koordinatensystem
Lineare Gleichungssysteme
2 Was ist ein Vektor? (1/2)
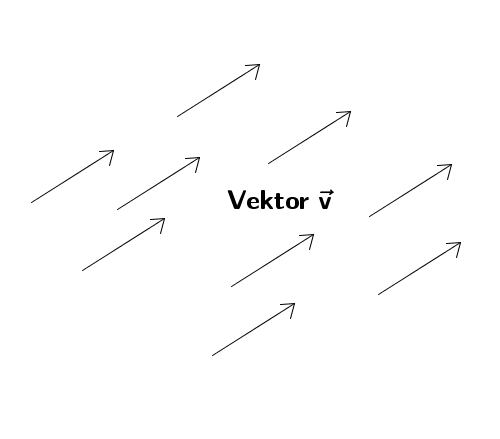
Ein Vektor bezeichnet eine Verschiebung in der Ebene oder im Raum und wird durch einen Pfeil repräsentiert, dessen Länge und Richtung genau die Länge und Richtung der Verschiebung ist.
Alle Pfeile, die parallel sind, die gleiche Länge haben und in dieselbe Richtung zeigen, repräsentieren denselben Vektor.
3 Was ist ein Vektor? (2/2)
Darstellung
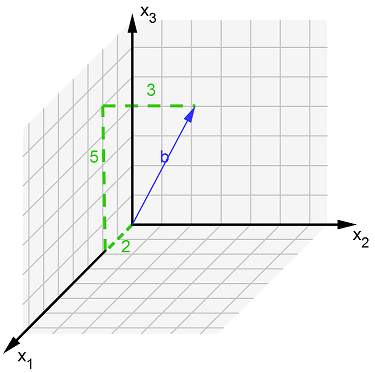
In der Schule werden schwerpunktmäßig Vektoren aus dem zweidimensionalen und dreidimensionalen Raum betrachtet.

4 Was ist ein Vektorraum?
Ein Vektorraum ist die Menge aller Vektoren mit einer bestimmten Anzahl an Einträgen. Man schreibt für die Menge der Vektoren in der Ebene, also und für die Menge der Vektoren im Raum, also .
5 Vektoren addieren (1/3)
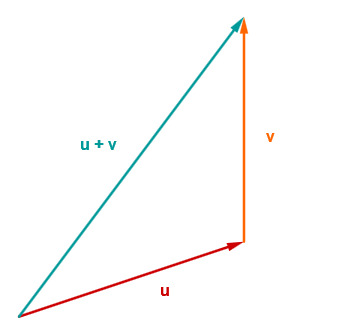
Vektoren addiert man, indem man sie aneinanderhängt. Dabei setzt man den Fuß des einen Vektors an die Spitze des anderen.
Die Summe von zwei Vektoren u und v entspricht also dem Vektor, der entsteht, wenn man vom Ursprung aus zuerst in Richtung u entlang geht und dann in Richtung v.
6 Vektoren addieren (2/3)
Vorgehensweise
Vektoren addiert man komponentenweise.
Der erste Eintrag des einen Vektors wird mit dem ersten Eintrag des anderen Vektors addiert. Danach der zweite Eintrag des einen mit dem zweiten des anderen und so weiter.
Das heißt, man addiert den n-ten Eintrag des einen Vektors mit dem n-ten Eintrag des anderen.
Beispiel
7 Vektoren addieren (3/3)
Bemerkung
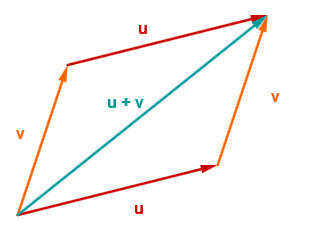
Anhand des Bildes sieht man, dass die Addition von Vektoren kommutativ ist. Das heißt, es ist egal, in welcher Reihenfolge man vorgeht.
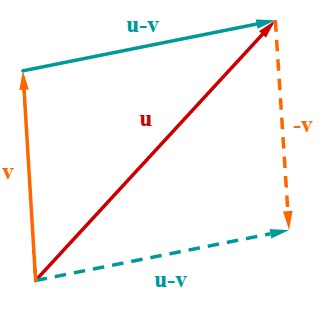
8 Vektoren subtrahieren (1/3)
Vektoren subtrahiert man, indem man ihre Spitzen verbindet.
Dabei setzt man für beide Vektoren denselben Fuß, die Spitze des Lösungsvektors ist dann die Spitze des Minuenden, der Fuß des Lösungsvektors ist die Spitze des Subtrahenden.
Die Differenz eines Vektors v von einem Vektor u entspricht also dem Vektor, der entsteht, wenn man vom Ursprung aus zuerst in Richtung u entlang geht und dann in Richtung -v.
9 Vektoren subtrahieren (2/3)
Vorgehensweise
Vektoren subtrahiert man komponentenweise.
Der erste Eintrag des Lösungsvektors ist die Differenz der ersten Einträge der subtrahierenden Vektoren, der zweite Einträg ist die Differenz der zweiten Einträge und so weiter.
Der n-te Eintrag des Lösungsvektors ist also die Differenz der n-ten Einträge der zu subtrahierenden Vektoren.
Beispiel
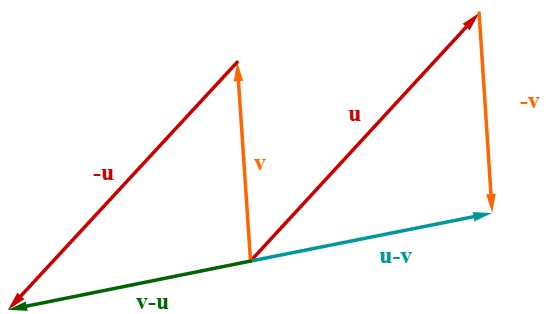
10 Vektoren subtrahieren (3/3)
Bemerkung
Die Subtraktion von Vektoren ist genauso wie die normale Subtraktion nicht kommutativ, wie das rechte Bild zeigt. Vertauscht man Minuend und Subtrahend, so zeigt der Lösungsvektor in die entgegengesetzte Richtung.
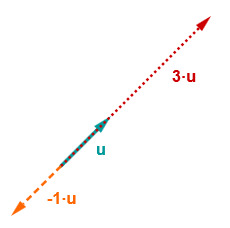
11 Vektoren mit einem Skalar multiplizieren (1/3)
Durch die Multiplikation eines Vektors mit einem Skalar, auch Linearfaktor genannt, wird der Vektor gestaucht oder gestreckt.
Der neue Vektor zeigt anschließend entweder in die gleiche oder in die genau entgegengesetzte Richtung.
12 Vektoren mit einem Skalar multiplizieren (2/3)
Vorgehensweise
Der Skalar, der immer ein Element aus sein muss, wird mit jeder Komponente des Vektors multipliziert.
Beispiel
13 Vektoren mit einem Skalar multiplizieren (3/3)
Bemerkung
Es ist egal, von welcher Seite der Skalar an den Vektor multipliziert wird.
Natürlich kann man auch Skalare aus einem Vektor "rausziehen".
14 Aufgaben zum Rechnen mit Vektoren
Laden
Laden
Laden
Laden
15 Linearkombination (1/2)
Eine Linearkombination von Vektoren ist eine Summe von Vektoren, wobei jeder Vektor noch mit einem Skalar (Linearfaktor) multipliziert wird. Das Ergebnis hiervon ist wieder ein Vektor.
Definition
Mit , und und Vektoren und ist eine Linearkombination der Vektoren .
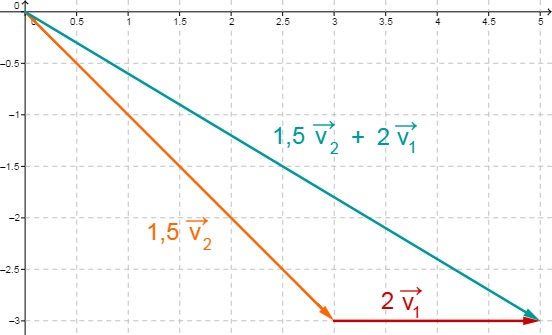
16 Linearkombination (2/2)
Beispiel
Mit , , und ist eine Linearkombination
.
17 Aufgaben zur Linearkombination
Laden
18 Vektor zwischen zwei Punkten berechnen (1/2)
Vorgehensweise
Um den Verbindungsvektor zwischen zwei Punkten A und B zu berechnen muss man den Ortsvektor vom Ortsvektor subtrahieren.
Man schreibt .
Dabei hat der Verbindungsvektor die Spitze im Minuend und den Fuß im Subtrahend. Als Merksatz gilt also
19 Vektor zwischen zwei Punkten berechnen (2/2)
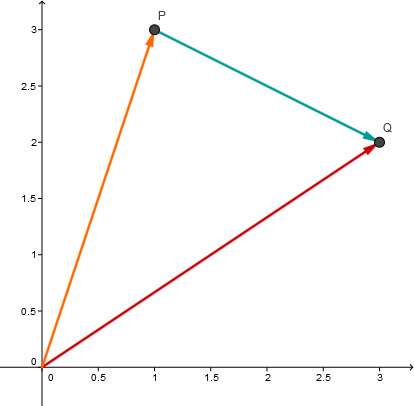
Beispiel
Berechne den Verbindungsvektor der Punkte und .
Der Verbindungsvektor wird als Differenzvektor berechnet. Dabei gilt die Regel:
"Spitze minus Fuß"
20 Aufgaben zum Berechnen eines Vektors zwischen zwei Punkten
Laden
21 Länge eines Vektors berechnen (1/3)
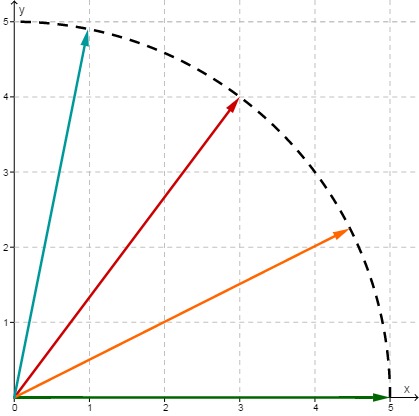
Die Länge eines Vektors ist der Abstand zwischen Spitze und Fuß. Die Länge wird auch als Betrag des Vektors bezeichnt. Die Berechnung erfolgt mit dem Satz von Pythagoras.
Die Vektoren in der Abbildung haben alle dieselbe Länge 5.
22 Länge eines Vektors berechnen (2/3)
Vorgehensweise
Die Länge eines Vektors berechnet man mit dem Satz des Pythagoras.
Man quadriert alle Komponenten des Vektors, addiert sie dann und zieht die Wurzel aus der Summe.
Formel
2-Dimensional | 3-Dimensional |
|---|---|
Für gilt | Für gilt |
23 Länge eines Vektors berechnen (3/3)
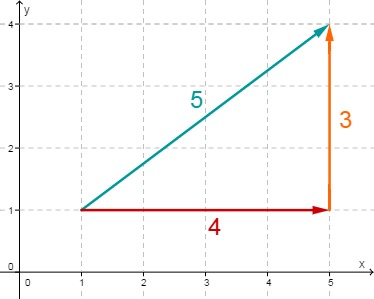
Beispiel
Für gilt
Bemerkung
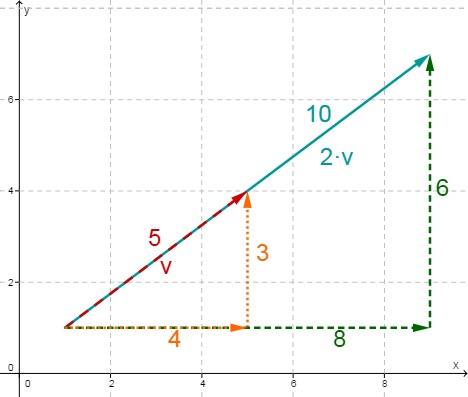
Multipliziert man einen Vektor mit einem Skalar , so wird auch seine Länge mit dem Faktor multipliziert.
24 Aufgaben zum Berechnen der Länge eines Vektors
Laden
25 Skalarprodukt (1/2)
Das Skalarprodukt ist eine Art der Multiplikation von Vektoren. Das Ergebnis ist eine reelle Zahl (im Gegensatz zum Kreuzprodukt, dessen Ergebnis wieder ein Vektor ist).
Definition
Um das Skalarprodukt von zwei Vektoren a und b zu berechnen, multipliziert man deren Einträge komponentenweise und addiert die Ergebnisse.
Man schreibt oder .
2-dimensional | 3-dimensional |
|---|---|
26 Skalarprodukt (2/2)
Verwendung des Skalarprodukts
Um Winkel zu berechnen | Um die Länge eines Vektors zu berechnen | |
|---|---|---|
Es gilt Dabei ist der Winkel, den beide Vektoren miteinander einschließen. Durch Umstellen der Gleichung lässt sich also der Winkel berechnen. | Mit Hilfe des Skalarprodukts lässt sich überprüfen, ob zwei Vektoren senkrecht zueinander stehen. Das ist genau dann der Fall, wenn ihr Skalarprodukt gleich Null ist. Es gilt | Die Länge eines Vektors ist gleich der Wurzel des Skalarprodukts des Vektors mit sich selbst. Das heißt . |
27 Aufgaben zum Skalarprodukt
Laden
28 Kreuzprodukt (1/3)
Das Kreuzprodukt ist eine Art der Multiplikation von dreidimensionalen Vektoren. Das Ergebnis ist ein neuer Vektor, der senkrecht auf den beiden vorigen steht.
Definition
Das Kreuzprodukt zweier Vektoren und wird mit bezeichnet und berechnet sich wie folgt.
29 Kreuzprodukt (2/3)
Beispiel
Für und ist das Kreuzprodukt
Vertauscht man die Reihenfolge der Vektoren, so ändert sich das Vorzeichen. In diesem Beispiel also .
30 Kreuzprodukt (3/3)
Bemerkung
Für das Kreuzprodukt gelten folgende Rechengesetze
31 Aufgaben zum Kreuzprodukt
Laden
32 Winkel zwischen Vektoren berechnen (1/2)
Den Winkel zwischen zwei Vektoren und entspricht dem Arkuskosinus vom Skalarprodukt der Vektoren geteilt durch das Produkt ihrer Längen.
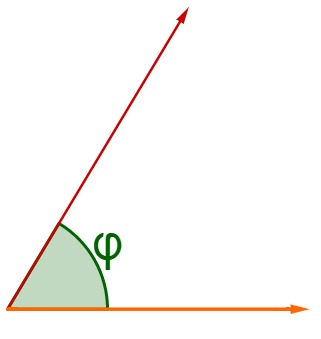
Formel
Für zwei Vektoren lässt sich der eingeschlossene WInkel mit folgender Formel berechnen.
33 Winkel zwischen Vektoren berechnen (2/2)
Beispiel
Die Vektoren und schließen einen Winkel von ein.
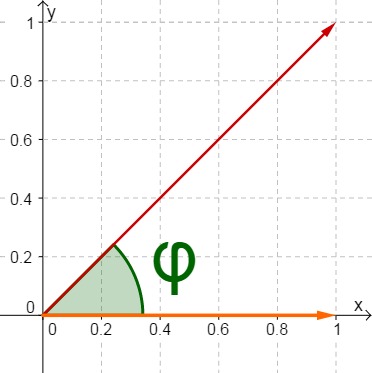
34 Aufgaben zum Berechnen des Winkels zwischen Vektoren
Laden
35 Lineare (Un)abhängigkeit (1/3)
Definition
Für zwei Vektoren
Man nennt zwei Vektoren linear abhängig, wenn sie kollinear sind, das heißt parallel verlaufen. Andernfalls nennt man sie linear unabhängig.
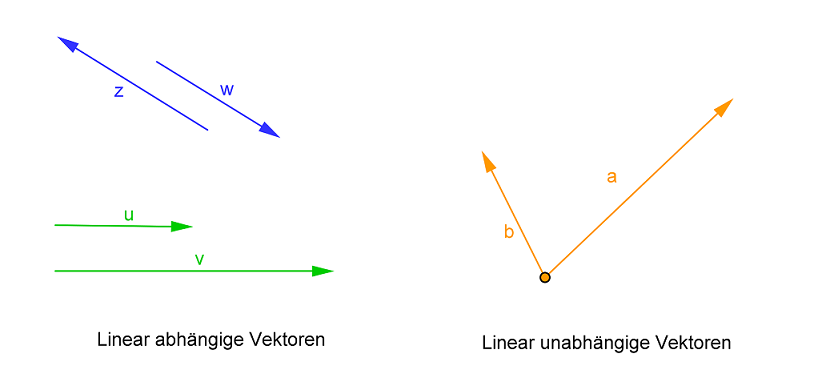
36 Lineare (Un)abhängigkeit (2/3)
Definition
Für drei Vektoren
Man nennt drei Vektoren linear abhängig, wenn sie komplanar sind, das heißt in einer Ebene liegen. Ist das der Fall, kann man mit ihnen durch Linearkombination eine geschlossene Vektorkette bilden. Andernfalls nennt man sie linear unabhängig.
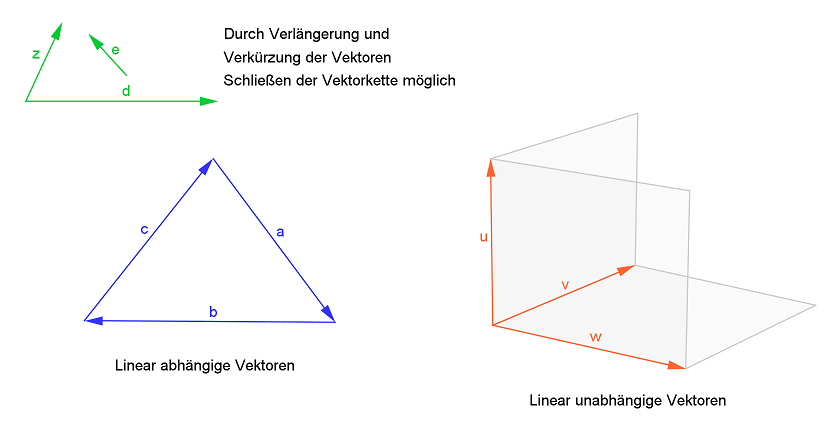
37 Lineare (Un)abhängigkeit (3/3)
Allgemeine Definition
Im Allgemeinen nennt man eine Menge von Vektoren linear abhängig, wenn man eine Linearkombination von ihnen bilden kann, die den Nullvektor ergibt und nicht trivial ist (trivial bedeutet hier, dass jeder Vektor mit Null multipliziert wird).
Ist das nicht möglich, nennt man die Vektoren linear unabhängig.
38 Aufgaben zur linearen (Un)abhängigkeit
Laden
39 Zusammenfassung
Formelsammlung
Ausblick/weiterführende Kurse
