1 Lösung 1c
Aufgabenstellung
Gegeben ist die in definierte Funktion . Der Graph von wird mit bezeichnet.
Bestimmen Sie die Koordinaten des Schnittpunkts von mit der -Achse und begründen Sie, dass oberhalb der -Achse verläuft. (2 BE) Ermitteln Sie das Symmetrieverhalten von sowie das Verhalten von für und für . (3 BE)
Zeigen Sie, dass für die zweite Ableitung von die Beziehung für gilt. Weisen Sie nach, dass linksgekrümmt ist. (4 BE)
Lösung
Zweite Ableitung von
Um die zweite Ableitung zu bestimmen, benötigst du zunächst die erste Ableitung. Beachte dazu die Ableitungsregeln.
Fasse so weit wie möglich zusammen.
Kannst du noch etwas ausklammern?
Damit bist du beim Kontrollergebnis.
Leite die Ableitung noch einmal ab. Beachte wieder die Ableitungsregeln.
Kannst du noch etwas ausklammern? Achte auf die Vorzeichen.
In der Klammer steht die Funktionsgleichung von . Daraus folgt:
Linkskrümmung nachweisen
Damit eine Linkskrümmung vorliegt, muss die zweite Ableitung immer positiv sein.
Du hast schon gezeigt, dass die Funktion immer oberhalb der -Achse verläuft, also gilt immer:
Daraus folgt:
Und damit gilt dann auch:
ist linksgekrümmt
2 Lösung 1d
Aufgabenstellung
Gegeben ist die in definierte Funktion . Der Graph von wird mit bezeichnet.
Bestimmen Sie die Koordinaten des Schnittpunkts von mit der -Achse und begründen Sie, dass oberhalb der -Achse verläuft. (2 BE)
Ermitteln Sie das Symmetrieverhalten von sowie das Verhalten von für und für . (3 BE)
Zeigen Sie, dass für die zweite Ableitung von die Beziehung für gilt. Weisen Sie nach, dass linksgekrümmt ist. (4 BE)
Zur Kontrolle:
Lösung
Lage des Extrempunkts
Du kannst dir jetzt schon überlegen, dass es nur einen einzigen Extrempunkt geben kann, weil der ganze Graph linksgekrümmt ist.
Suche den Extrempunkt, indem du die Nullstelle der ersten Ableitung suchst:
Setze :
Das Ergebnis ist auf beiden Seiten gleich, wenn die Exponenten gleich sind. Dies kannst du dir entweder aus den Potenzgesetzen herleiten oder du wendest den natürlichen Logarithmus auf beiden Seiten der Gleichung an:
Diese Gleichung ist nur für erfüllt.
Da in schon der -Achsenabschnitt () berechnet wurde ergibt sich der Extrempunkt .
Art des Extrempunkts
In wurde bereits gezeigt, dass ist (dies gilt also insbesondere auch für ), also handelt es sich um einen Tiefpunkt.
3 Lösung 1e
Aufgabenstellung
Gegeben ist die in definierte Funktion . Der Graph von wird mit bezeichnet.
Bestimmen Sie die Koordinaten des Schnittpunkts von mit der -Achse und begründen Sie, dass oberhalb der -Achse verläuft. (2 BE)
Ermitteln Sie das Symmetrieverhalten von sowie das Verhalten von für und für . (3 BE)
Zeigen Sie, dass für die zweite Ableitung von die Beziehung für gilt. Weisen Sie nach, dass linksgekrümmt ist. (4 BE)
Zur Kontrolle:
Bestimmen Sie Lage und Art des Extrempunkts von . (3 BE)
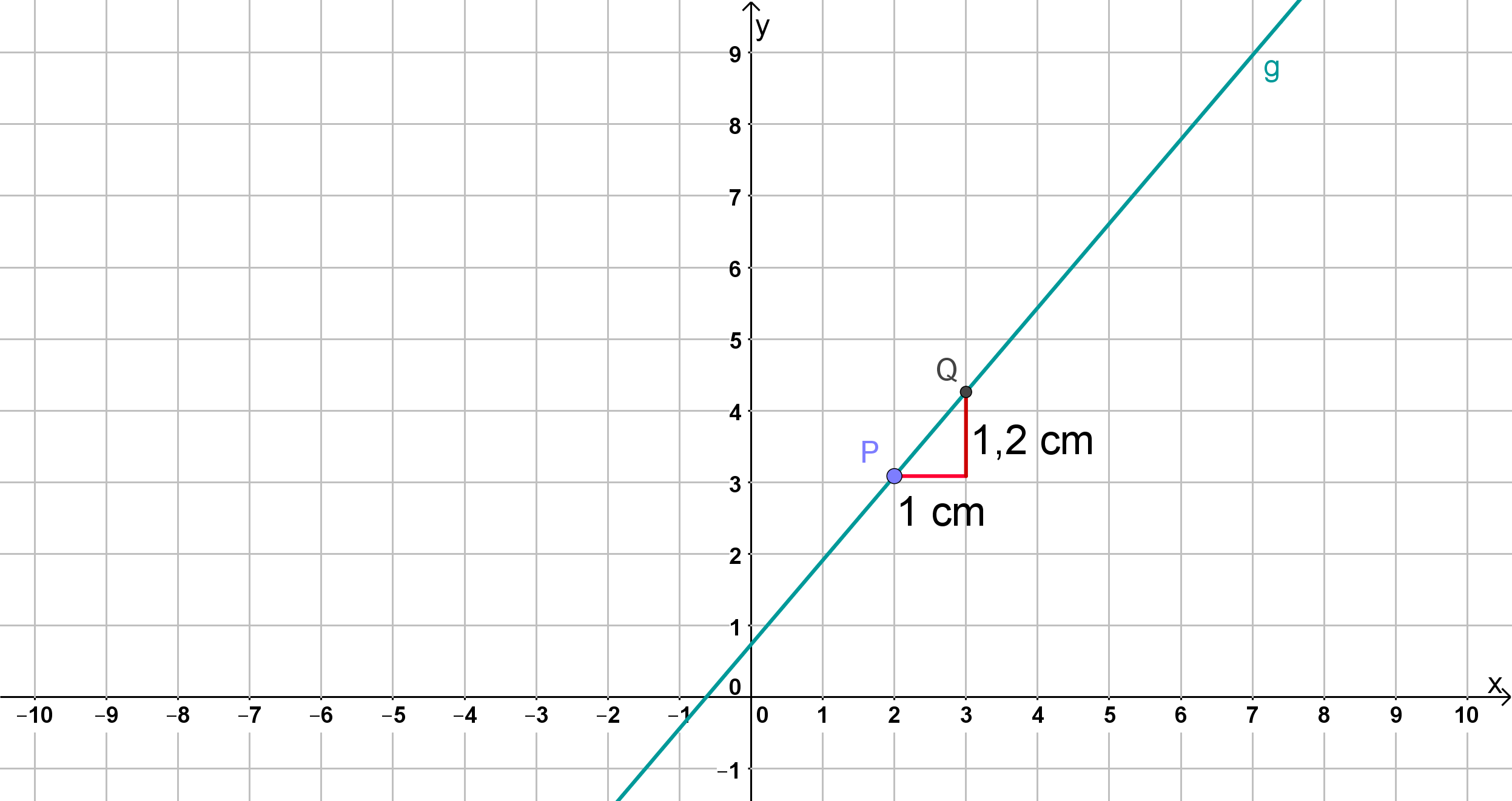
e) Berechnen Sie die Steigung der Tangente an im Punkt auf eine Dezimale genau. Zeichnen Sie den Punkt und die Gerade in ein Koordinatensystem ein (Platzbedarf im Hinblick auf das Folgende: , ). (3 BE)
Lösung
Berechnen der Tangentensteigung
Die Steigung der Tangente ist per Definition gleich zur Ableitung in einem Punkt. Setze also in die erste Ableitung ein.
Die Steigung ist also .
Zeichnen des Punktes und der Tangente
Bestimme zunächst die -Koordinate von .
Die Koordinaten des Punktes sind also .
Du zeichnest den Punkt Punkt in ein Koordinatensystem und bestimmst mit Hilfe eines Steigungsdreiecks einen weiteren Punkt . Diese beiden Punkte verbindest du zu der Geraden .
4 Lösung 1f
Aufgabenstellung
Gegeben ist die in definierte Funktion . Der Graph von wird mit bezeichnet.
Bestimmen Sie die Koordinaten des Schnittpunkts von mit der -Achse und begründen Sie, dass oberhalb der -Achse verläuft. (2 BE)
Ermitteln Sie das Symmetrieverhalten von sowie das Verhalten von für und für . (3 BE)
Zeigen Sie, dass für die zweite Ableitung von die Beziehung für gilt. Weisen Sie nach, dass linksgekrümmt ist. (4 BE)
Zur Kontrolle:
Bestimmen Sie Lage und Art des Extrempunkts von . (3 BE)
Berechnen Sie die Steigung der Tangente an im Punkt auf eine Dezimale genau. Zeichnen Sie den Punkt und die Gerade in ein Koordinatensystem ein (Platzbedarf im Hinblick auf das Folgende: , ). (3 BE)
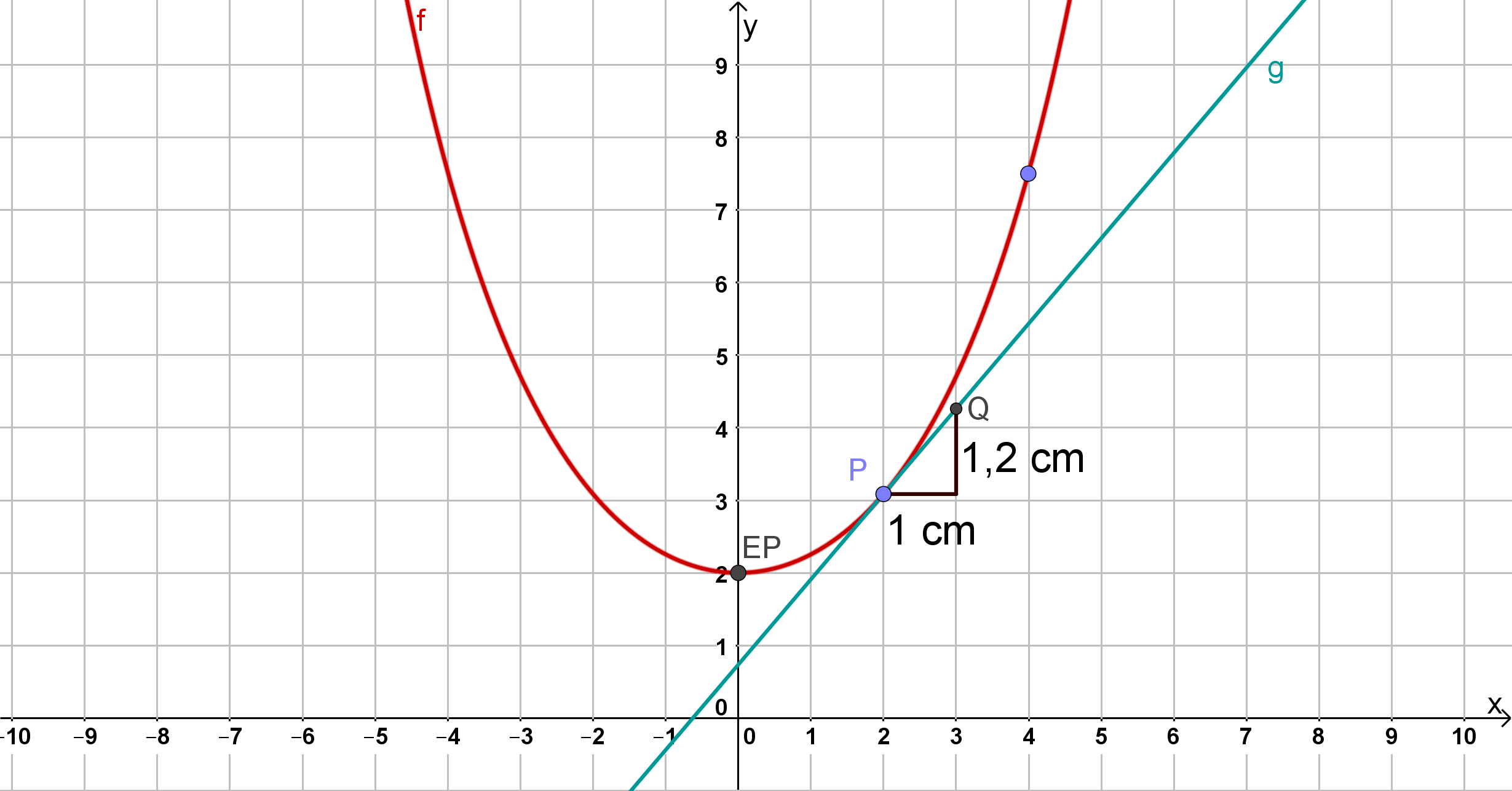
Berechnen Sie , im Hinblick auf eine der folgenden Aufgaben auf zwei Dezimalen genau, und zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse im Bereich in das Koordinatensystem aus Aufgabe 1e ein. (4 BE)
Lösung
Berechnung von
Graph von
Zeichne nun den Graphen, du kennst schon:
den Extrempunkt
den Punkt
den Punkt
das Verhalten im Unendlichen
die Symmetrie zur y-Achse
Insgesamt ergibt sich folgender Graph:
5 Lösung 1g
Aufgabenstellung
Gegeben ist die in definierte Funktion . Der Graph von wird mit bezeichnet.
Bestimmen Sie die Koordinaten des Schnittpunkts von mit der -Achse und begründen Sie, dass oberhalb der -Achse verläuft. (2 BE)
Ermitteln Sie das Symmetrieverhalten von sowie das Verhalten von für und für . (3 BE)
Zeigen Sie, dass für die zweite Ableitung von die Beziehung für gilt. Weisen Sie nach, dass linksgekrümmt ist. (4 BE)
Zur Kontrolle:
Bestimmen Sie Lage und Art des Extrempunkts von . (3 BE)
Berechnen Sie die Steigung der Tangente an im Punkt auf eine Dezimale genau. Zeichnen Sie den Punkt und die Gerade in ein Koordinatensystem ein (Platzbedarf im Hinblick auf das Folgende: , ). (3 BE)
Berechnen Sie , im Hinblick auf eine der folgenden Aufgaben auf zwei Dezimalen genau, und zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse im Bereich in das Koordinatensystem aus Aufgabe 1e ein. (4 BE)
Lösung
Rechnung
Setze ein und vereinfache.
Beachte, dass du jetzt die binomischen Formeln anwenden musst!
Überlege jetzt, wie sich die Exponenten zusammen addieren bzw. multiplizieren. Die Potenzgesetze helfen dir dabei.
Spätestens jetzt kannst du die aus der zweiten Klammer herausziehen und ganz ausklammern.
Spätestens jetzt kannst du wiederum die durch ersetzen. Vereinfache außerdem so weit wie möglich.
Geschafft! :) Damit ist die Gleichung gezeigt.
6 Lösung 1h
Aufgabenstellung
Gegeben ist die in definierte Funktion . Der Graph von wird mit bezeichnet.
Bestimmen Sie die Koordinaten des Schnittpunkts von mit der -Achse und begründen Sie, dass oberhalb der -Achse verläuft. (2 BE)
Ermitteln Sie das Symmetrieverhalten von sowie das Verhalten von für und für . (3 BE)
Zeigen Sie, dass für die zweite Ableitung von die Beziehung für gilt. Weisen Sie nach, dass linksgekrümmt ist. (4 BE)
Zur Kontrolle:
Bestimmen Sie Lage und Art des Extrempunkts von . (3 BE)
Berechnen Sie die Steigung der Tangente an im Punkt auf eine Dezimale genau. Zeichnen Sie den Punkt und die Gerade in ein Koordinatensystem ein (Platzbedarf im Hinblick auf das Folgende: , ). (3 BE)
Berechnen Sie , im Hinblick auf eine der folgenden Aufgaben auf zwei Dezimalen genau, und zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse im Bereich in das Koordinatensystem aus Aufgabe 1e ein. (4 BE)
Zeigen Sie durch Rechnung, dass für die Beziehung gilt. (3 BE)
Die als Kurvenlänge bezeichnete Länge des Funktionsgraphen von zwischen den Punkten und mit lässt sich mithilfe der Formel berechnen.
Bestimmen Sie mithilfe der Beziehung aus Aufgabe die Kurvenlänge des Graphen von zwischen den Punkten und mit b>0.
Lösung
Klingt wahnsinnig kompliziert, oder? Ist es aber wirklich nicht. Lass dich einfach nicht von so vielen Infos verwirren, sondern lies die Aufgabenstellung noch ein paar Mal in Ruhe durch und finde heraus, welche Informationen du wirklich benötigst. Du siehst ein Integral, dass du mit Hilfe der Beziehung aus Aufgabe lösen sollst. Sieh dir dazu an, was im Integral steht: . Wenn du genauer hin schaust, siehst du vielleicht, dass du die Beziehung aus so umformen kannst, dass du den Term unter der Wurzel bekommst. Fange damit an.
Umformung der Beziehung aus
Jetzt kannst du anstatt der rechten Seite, die unter der Wurzel im Integral steht, auch die linke Seite benutzen, da diese äquivalent sind.
Bestimmung des Integrals
Erinnere dich, auf was du bei der Berechnung eines Integrals alles achten musst. In dem Text über der Aufgabenstellung steht . In der Aufgabenstellung heißt es aber, du sollst ausrechnen. Die Grenzen des Integrals sind also nicht die gleichen.
Verändere jetzt die Wurzel mit der Beziehung aus die du gerade ausgerechnet hast.
Schau genau hin! Die Wurzel und das Quadrat kürzen sich und kannst du ebenfalls aus der Wurzel ziehen.
Setze ein.
Das kannst du als Vorfaktor aus dem Integral heraus ziehen.
Berechne das Integral. Erinnere dich, wie du die Exponentialfunktion aufleitest und wie du beim Integrieren "nachdifferenzierst".
Beachte:
Und schon bist du beim richtigen Ergebnis. Super gemacht! :)
7 Aufgabe 2 - Aufgabenstellung
Die Enden eines Seils werden an zwei vertikalen Masten, die voneinander entfernt sind, in gleicher Höhe über dem Erdboden befestigt. Der Graph aus Aufgabe 1 beschreibt im Bereich modellhaft den Verlauf des Seils, wobei die Fußpunkte und der Masten durch die Punkte bzw. dagestellt werden (vgl. Abbildung). Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
Der Höhenunterschied zwischen den Aufhängepunkten und dem tiefsten Punkt des Seils wird als Durchhang bezeichnet. Berechnen Sie auf der Grundlage des Modells den Durchhang des Seils auf Zentimeter genau. (2 BE)
Berechnen Sie auf der Grundlage des Modells die Größe des Winkels, den das Seil mit Mast 2 im Aufhängepunkt einschließt, sowie mithilfe der Kurvenlänge aus Aufgabe 1h die Länge des zwischen den Masten hängenden Seils auf Zentimeter genau. (5 BE)
Der Graph von soll durch eine Parabel näherungsweise dargestellt werden.Dazu wird die in definierte quadratische Funktion betrachtet, derenGraph den Scheitelpunkt hat und durch den Punkt verläuft.
Ermitteln Sie den Term der Funktion , ohne dabei zu runden. (4 BE)
Für jedes wird der Abstand der vertikal übereinander liegenden Punkte und der Graphen von bzw betrachtet, wobei in diesem Bereich gilt. Der größte dieser Abstände ist ein Maß dafür, wie gut die Parabel den Graphen im Bereich annähert. Beschreiben Sie die wesentlichen Schritte, mithilfe derer man diesen größten Abstand rechnerisch bestimmen kann. (3 BE)
8 Lösung 2a
Die Enden eines Seils werden an zwei vertikalen Masten, die voneinander entfernt sind, in gleicher Höhe über dem Erdboden befestigt. Der Graph aus Aufgabe 1 beschreibt im Bereich modellhaft den Verlauf des Seils, wobei die Fußpunkte und der Masten durch die Punkte bzw. dagestellt werden (vgl. Abbildung). Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
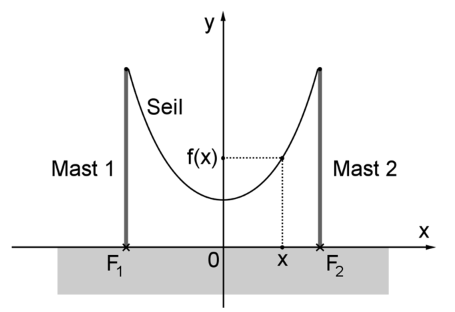
Der Höhenunterschied zwischen den Aufhängepunkten und dem tiefsten Punkt des Seils wird als Durchhang bezeichnet. Berechenen Sie auf der Grundlage des Modells den Durchhang des Seils auf Zentimeter genau. (2 BE)
Lösung
Berechnung des Durchhangs
In der Abbildung kann man erkennen, dass der tiefste Punkt des Seils bei liegt. Du musst also die Differenz berechnen. Aus Aufgabe 1 weißt du bereits:
Beachte hierbei, dass du auf zwei Dezimalen runden musst, wenn du eine Länge in Meter auf Zentimeter genau angeben sollst.
Länge des Durchhangs:
Die Länge des Durchhangs beträgt also und .
9 Lösung 2b
Die Enden eines Seils werden an zwei vertikalen Masten, die voneinander entfernt sind, in gleicher Höhe über dem Erdboden befestigt. Der Graph aus Aufgabe 1 beschreibt im Bereich modellhaft den Verlauf des Seils, wobei die Fußpunkte und der Masten durch die Punkte bzw. dagestellt werden (vgl. Abbildung). Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
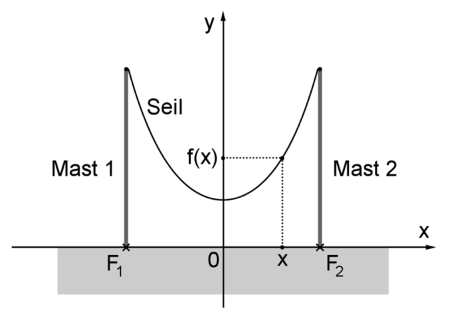
Der Höhenunterschied zwischen den Aufhängepunkten und dem tiefsten Punkt des Seils wird als Durchhang bezeichnet. Berechenen Sie auf der Grundlage des Modells den Durchhang des Seils auf Zentimeter genau. (2 BE)
Berechen Sie auf der Grundlage des Modells die Größe des Winkels, den das Seil mit Mast 2 im Aufhängepunkt einschließt, sowie mithilfe der Kurvenlänge aus Aufgabe 1h die Länge des zwischen den Masten hängenden Seils auf Zentimeter genau. (5 BE)
Lösung
Berechnung des Winkels
Um den Winkel zwischen dem Seil und dem Mast 2 auszurechnen, benötigst du zunächst die Tangente im Aufhängepunkt . Daraufhin kannst du im Steigungsdreieck mithilfe von Sinus und Kosinus den Winkel berechnen (siehe Abbildung). Da wir nur das Steigungsdreieck betrachten genügt es hierbei die Steigung der Tangente (also den Wert der Ableitung in dem Aufhängepunkt) zu bestimmen. Die Ableitungsfunktion hast du bereits in Aufgabe 1c bestimmt:
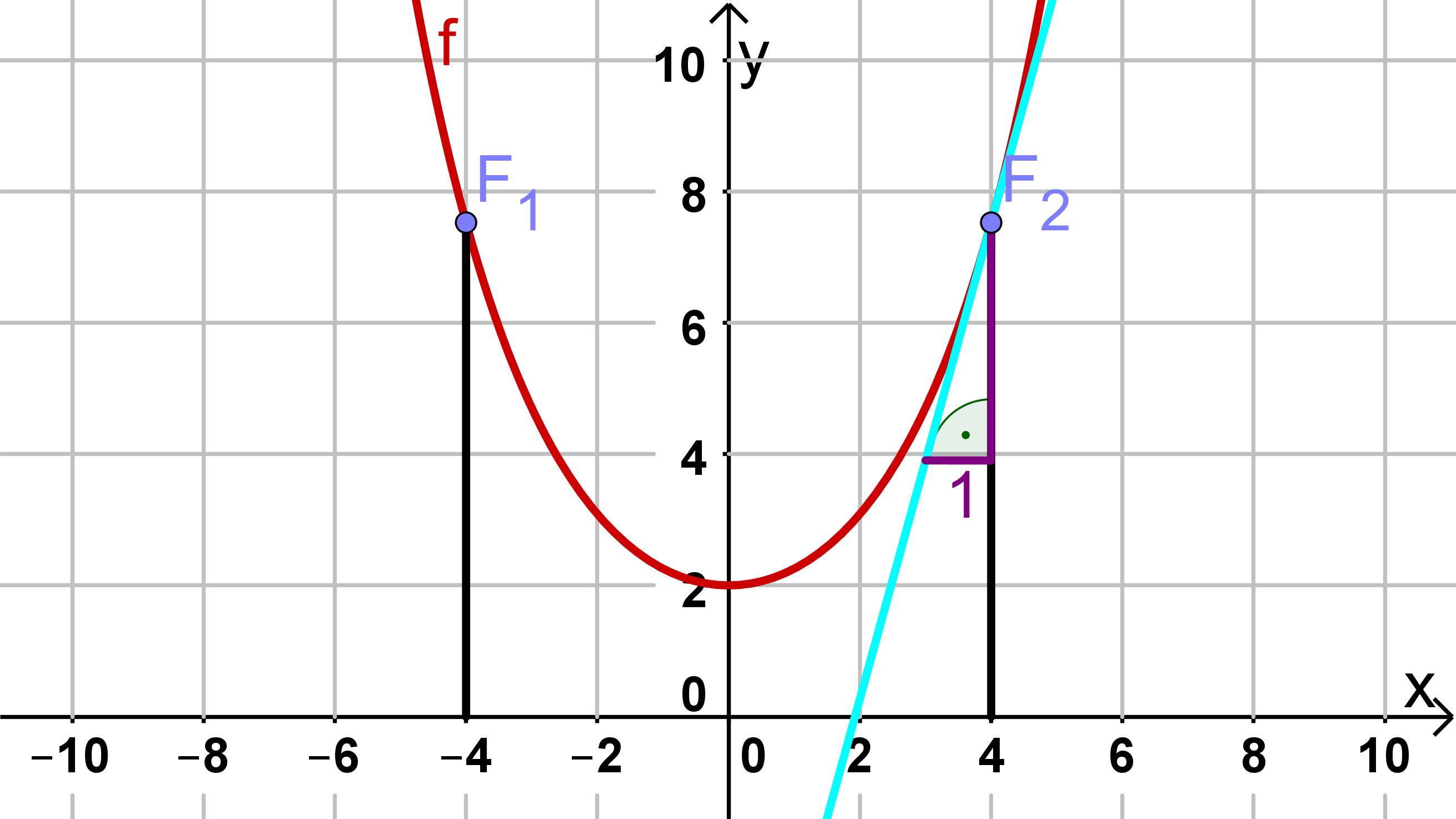
Bestimmung der Tangentensteigung im Aufhängepunkt:
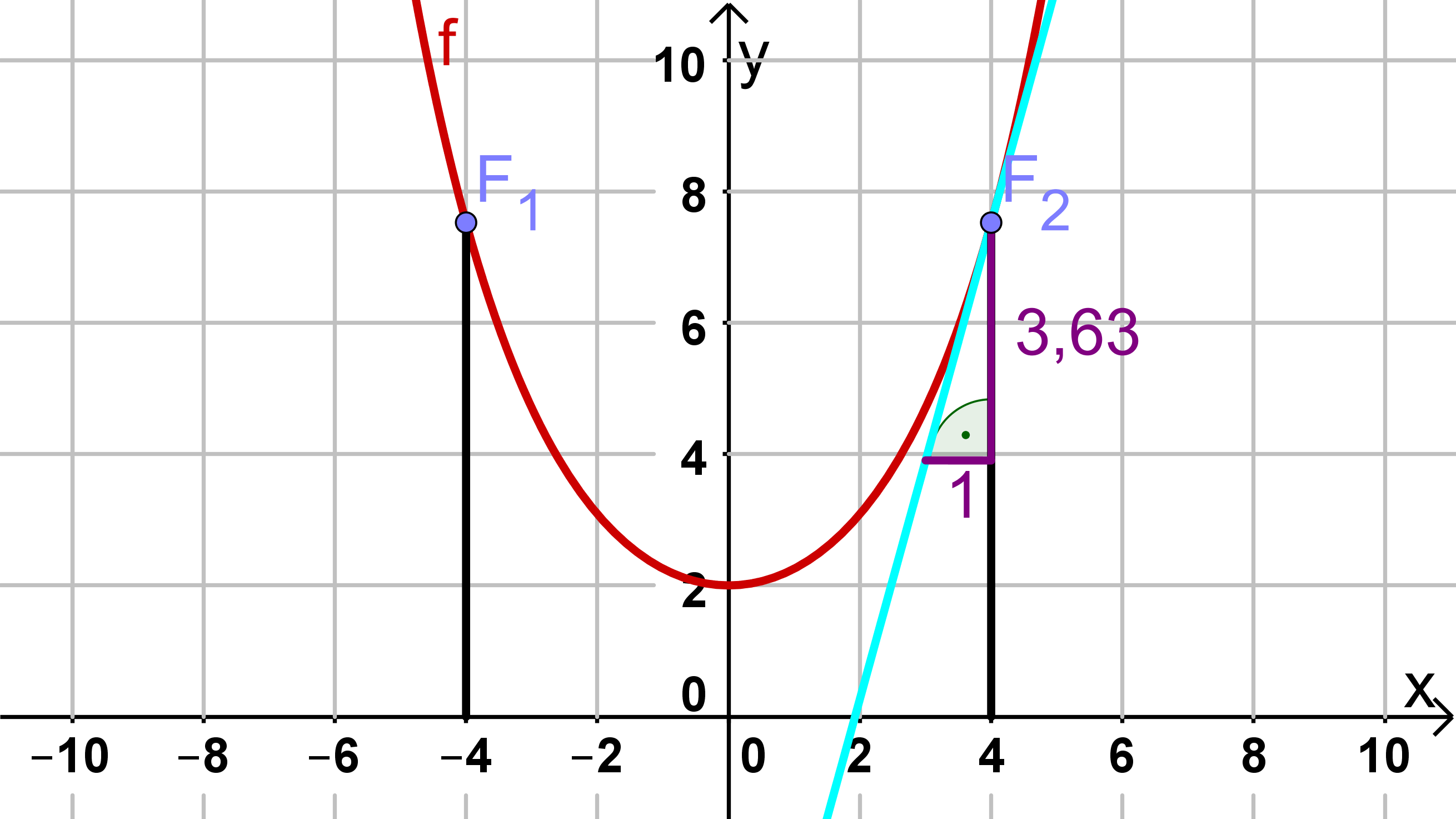
Du siehst nun in der Abbildung, dass du mit dem Steigungsdreieck ein rechtwinkliges Dreieck hast. Von diesem kennst du bereits zwei Seiten, die Gegenkathete und die Ankathete des gesuchten Winkels. Mithilfe der Formel kannst du zunächst den Tangens der Winkels und dann über die Umekehrfunktion des Tangens den gesuchten Winkel berechnen.
Die Umkehrfunktion des Tangens kannst du bei deinem Taschenrechner mit der Taste aufrufen.
Achte hierbei auch darauf, dass dein Taschenrechner auf Gradmaß und nicht auf Bogenmaß eingestellt ist!
Im Folgenden werden wir den gesuchten Winkel mit bezeichnen.
Berechnung des Tangens:
Berechnung des Winkels mithilfe der Umkehrfunktion des Tangens:
Das Seil schließt mit dem Mast im Aufhängepunkt 2 einen Winkel von ca. ein.
Berechnung der Seillänge
Aus Aufgabe 1h hast du bereits die Formel . Außerdem siehst du, dass der Graph achsensymmetrisch zur -Achse ist. Also kannst du statt der Länge zwischen den beiden Masten auch die einem Masten und dem Tiefpunkt berechnen und diese dann verdoppeln:
Beachte, dass du wieder auf zwei Nachkommastellen runden musst.
Länge des Seils in Meter:
Die Länge des Seils zwischen den beiden Masten beträgt Meter und Zentimeter.
10 Lösung 2c
Die Enden eines Seils werden an zwei vertikalen Masten, die voneinander entfernt sind, in gleicher Höhe über dem Erdboden befestigt. Der Graph aus Aufgabe 1 beschreibt im Bereich modellhaft den Verlauf des Seils, wobei die Fußpunkte und der Masten durch die Punkte bzw. dagestellt werden (vgl. Abbildung). Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
Der Höhenunterschied zwischen den Aufhängepunkten und dem tiefsten Punkt des Seils wird als Durchhang bezeichnet. Berechenen Sie auf der Grundlage des Modells den Durchhang des Seils auf Zentimeter genau. (2 BE)
Berechen Sie auf der Grundlage des Modells die Größe des Winkels, den das Seil mit Mast 2 im Aufhängepunkt einschließt, sowie mithilfe der Kurvenlänge aus Aufgabe 1h die Länge des zwischen den Masten hängenden Seils auf Zentimeter genau. (5 BE)
Dazu wird die in definierte quadratische Funktion betrachtet, derenGraph den Scheitelpunkt hat und durch den Punkt verläuft.
Lösung
Quadratische Funktion erstellen
Aus der Angabe kannst du den Scheitelpunkt übernehmen. Trage diesen in die Scheitelform ein. Diese lautet mit dem Scheitelpunkt .
Setze ein.
Du findest heraus, indem du den gegebenen Punkt einsetzt und nach auflöst.
Setze alle Werte ein, damit du eine vollständige quadratische Funktion erhältst.
11 Lösung 2d
Die Enden eines Seils werden an zwei vertikalen Masten, die voneinander entfernt sind, in gleicher Höhe über dem Erdboden befestigt. Der Graph aus Aufgabe 1 beschreibt im Bereich modellhaft den Verlauf des Seils, wobei die Fußpunkte und der Masten durch die Punkte bzw. dagestellt werden (vgl. Abbildung). Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
Der Höhenunterschied zwischen den Aufhängepunkten und dem tiefsten Punkt des Seils wird als Durchhang bezeichnet. Berechenen Sie auf der Grundlage des Modells den Durchhang des Seils auf Zentimeter genau. (2 BE)
Berechen Sie auf der Grundlage des Modells die Größe des Winkels, den das Seil mit Mast 2 im Aufhängepunkt einschließt, sowie mithilfe der Kurvenlänge aus Aufgabe 1h die Länge des zwischen den Masten hängenden Seils auf Zentimeter genau. (5 BE)
Der Graph von soll durch eine Parabel näherungsweise dargestellt werden.Dazu wird die in definierte quadratische Funktion betrachtet, derenGraph den Scheitelpunkt hat und durch den Punkt verläuft.
Ermitteln Sie den Term der Funktion , ohne dabei zu runden. (4 BE)
Für jedes wird der Abstand der vertikal übereinander liegenden Punkte und der Graphen von bzw betrachtet, wobei in diesem Bereich gilt. Der größte dieser Abstände ist ein Maß dafür, wie gut die Parabel den Graphen im Bereich annähert. Beschreiben Sie die wesentlichen Schritte, mithilfe derer man diesen größten Abstand rechnerisch bestimmen kann. (3 BE)
Lösung
Den Abstand zwischen zwei Funktionen bestimmst du, indem du die beiden Funktionen ganz einfach voneinander abziehst. Anschließend bekommst du daraus eine neue Funktion. Diese Funktion kannst du ableiten und das Maximum berechnen, indem du die Ableitung Null setzt. (Hierbei musst du darauf achten, dass sich das Maximum in dem angegebenen Intervall liegt.) Wenn du dann noch die zweite Ableitung ausrechnest, hast du bewiesen, dass es sich bei dem Extrempunkt aus der ersten Ableitung auf jeden Fall um ein Maximum und nicht um ein Terrassenpunkt handelt.
Schritte:
Funktionen voneinander abziehen. Betrag nehmen, dann ist die Reihenfolge egal ()
Ableitung der neuen Funktion bilden und Null setzen
Extrempunkt herausfinden (sollte im Intervall liegen)
Zweite Ableitung bilden und Extrempunkt (Maximum) bestätigen
