Berechne für folgende Parabeln die Nullstellen, den Scheitelpunkt mithilfe der quadratischen Ergänzung und die Achsenschnittpunkte. Zeichnen Sie den Graphen unter zu Hilfenahme des Scheitelpunkts.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Quadratische Ergänzung
Um den Scheitelpunkt aus der Scheitelform zu bestimmen, muss eine quadratische Ergänzung mit dem Funktionsterm durchgeführt werden.
↓ ↓ In eine Binomische Formel umschreiben.
Scheitelpunkt:
Nullstellen berechnen
Das Berechnen der Nullstellen funktioniert für quadratische Funktionen allgemein immer mit der Mitternachtsformel. In manchen speziellen Fällen kann aber auch der Satz von Vieta zu einer schnellen Lösung führen.
Setze . Satz von Vieta anwenden.
Schnittpunkt mit der x-Achse
Wenn man die Nullstellen berechnet hat, folgt daraus, dass der y-Wert 0 sein muss.
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu berechnen, muss der x-Wert gleich 0 sein.
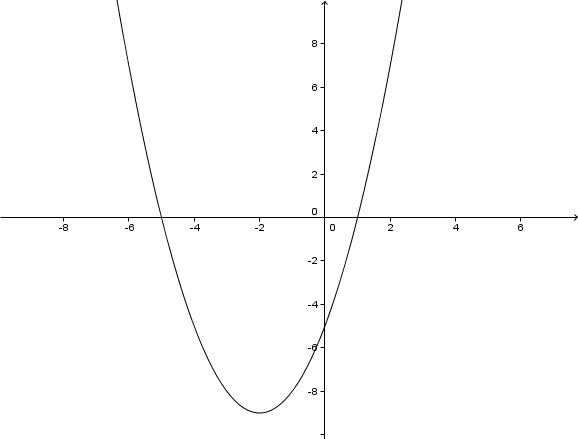
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Quadratische Ergänzung
Um den Scheitelpunkt aus der Scheitelform zu bestimmen, muss eine quadratische Ergänzung mit dem Funktionsterm durchgeführt werden.
↓ Minus ausklammern. Distributivgesetz.
↓ ↓ In eine Binomische Formel umschreiben.
↓ Zusammenfassen
↓ Ausmultiplizieren
Scheitelpunkt:
Nullstellen berechnen
Das Berechnen der Nullstellen funktioniert für quadratische Funktionen allgemein immer mit der Mitternachtsformel. In manchen speziellen Fällen kann aber auch der Satz von Vieta zu einer schnellen Lösung führen.
Setze f(x)=0. Minus ausklammern. Distributivgesetz.
Satz von Vieta anwenden.
Schnittpunkt mit der x-Achse
Wenn man die Nullstellen berechnet hat, folgt daraus, dass der y-Wert 0 sein muss.
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu berechnen, muss der x-Wert gleich 0 sein.
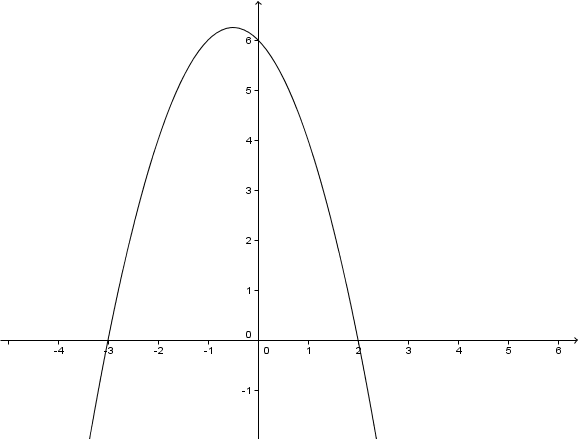
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Quadratische Ergänzung
Um den Scheitelpunkt aus der Scheitelform zu bestimmen, muss eine quadratische Ergänzung mit dem Funktionsterm durchgeführt werden.
↓ Minus ausklammern. Distributivgesetz.
↓ ↓ In eine Binomische Formel umschreiben.
↓ Zusammenfassen
Scheitelpunkt:
Nullstellen berechnen
Das Berechnen der Nullstellen funktioniert für quadratische Funktionen allgemein immer mit der Mitternachtsformel. In manchen speziellen Fällen, kann aber auch der Satz von Vieta zu einer schnellen Lösung führen.
Setze . Minus ausklammern. Distributivgesetz.
Satz von Vieta anwenden.
Doppelte Nullstelle
Schnittpunkt mit der x-Achse
Wenn man die Nullstellen berechnet hat, folgt daraus, dass der y-Wert 0 sein muss.
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu berechnen, muss der x-Wert gleich 0 sein.
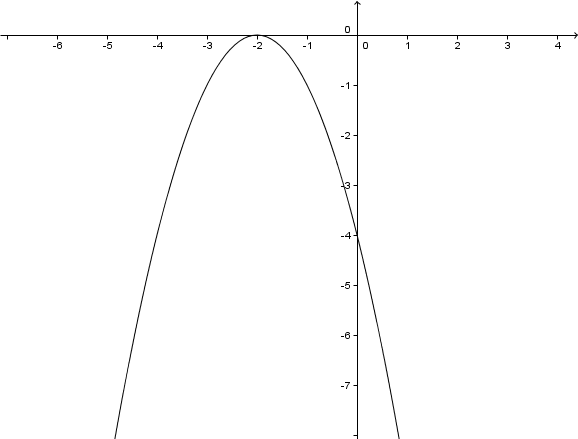
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Quadratische Ergänzung
Um den Scheitelpunkt aus der Scheitelform zu bestimmen, muss eine quadratische Ergänzung mit dem Funktionsterm durchgeführt werden.
↓ ausklammern. Distributivgesetz
↓ ↓ In eine Binomische Formel umschreiben
↓ Zusammenfassen
↓ Ausmultiplizieren
Scheitelpunkt:
Nullstellen berechnen
Das Berechnen der Nullstellen funktioniert für quadratische Funktionen allgemein immer mit der Mitternachtsformel. In manchen speziellen Fällen, kann aber auch der Satz von Vieta zu einer schnellen Lösung führen.
Setze .
ausklammern. Distributivgesetz.
↓ ↓ Schnittpunkt mit der x-Achse
Wenn man die Nullstellen berechnet hat, folgt daraus, dass der y-Wert 0 sein muss.
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu berechnen, muss der x-Wert gleich 0 sein.
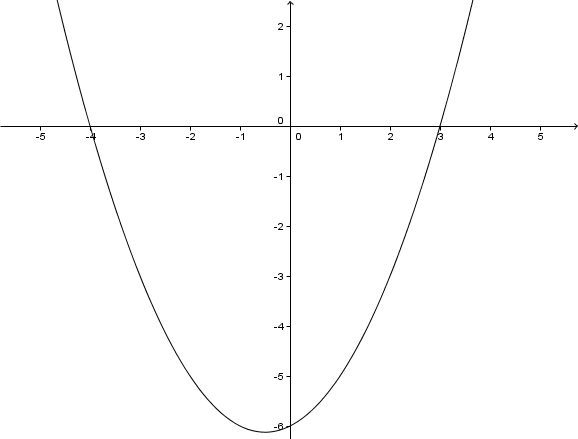
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Quadratische Ergänzung
Um den Scheitelpunkt aus der Scheitelform zu bestimmen, muss eine quadratische Ergänzung mit dem Funktionsterm durchgeführt werden.
↓ ausklammern. Distributivgesetz.
↓ ↓ In eine Binomische Formel umschreiben.
↓ Distributivgesetz. anwenden.
Scheitelpunkt:
Nullstellen berechnen
Das Berechnen der Nullstellen funktioniert für quadratische Funktionen allgemein immer mit der Mitternachtsformel.
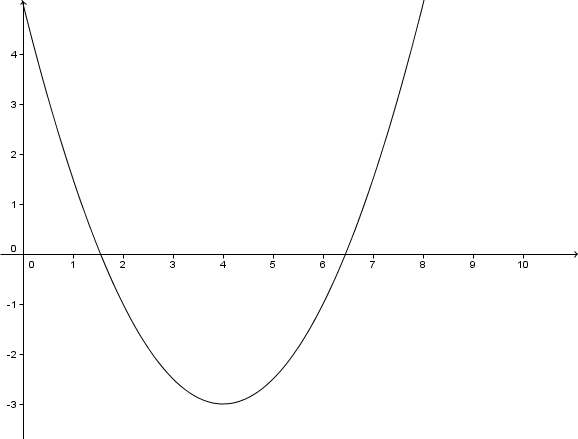
Setze . Mitternachtsformel anwenden. Dafür die Diskriminante D berechnen.
2 Lösungen
Mitternachtsformel anwenden.
Schnittpunkt mit der x-Achse
;
Wenn man die Nullstellen berechnet hat, folgt daraus, dass der y-Wert 0 sein muss.
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu berechnen, muss der x-Wert gleich 0 sein.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Quadratische Ergänzung
Um den Scheitelpunkt aus der Scheitelform zu bestimmen, muss eine quadratische Ergänzung mit dem Funktionsterm durchgeführt werden.
↓ ↓ In eine Binomische Formel umschreiben.
Scheitelpunkt:
Nullstellen berechnen
Das Berechnen der Nullstellen funktioniert für quadratische Funktionen allgemein immer mit der Mitternachtsformel.
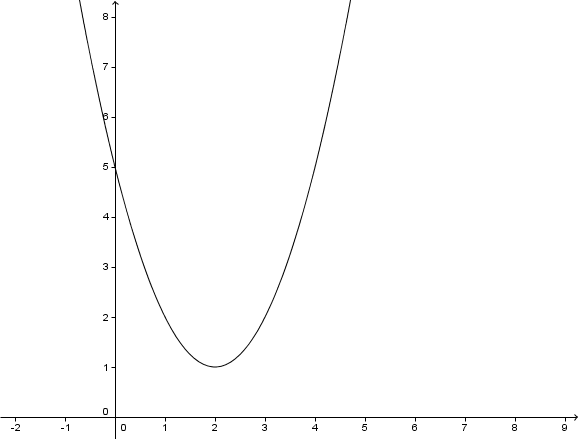
Setze . Mitternachtsformel anwenden. Dafür die Diskriminante D berechnen.
keine Lösung
Schnittpunkt mit der x-Achse
keine Lösung. Da es keine Nullstelle gibt, kann es auch keinen Schnittpunkt mit der x-Achse geben.
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu berechnen, muss der x-Wert gleich 0 sein.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Quadratische Ergänzung
Um den Scheitelpunkt aus der Scheitelform zu bestimmen, muss eine quadratische Ergänzung mit dem Funktionsterm durchgeführt werden.
↓ ausklammern. Distributivgesetz.
↓ ↓ In eine Binomische Formel umschreiben.
↓ Distributivgesetz anwenden.
↓ Zusammenfassen
Scheitelpunkt:
Nullstellen berechnen
Das Berechnen der Nullstellen funktioniert für quadratische Funktionen allgemein immer mit der Mitternachtsformel.
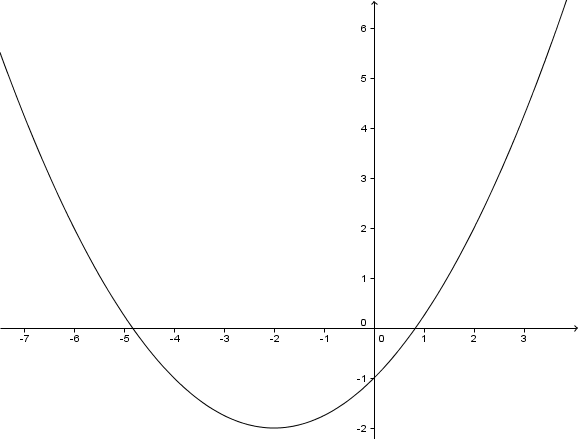
Setze . Mitternachtsformel anwenden. Dafür die Diskriminante D berechnen.
2 Lösungen
Mitternachtsformel anwenden.
Schnittpunkt mit der x-Achse
;
Wenn man die Nullstellen berechnet hat, folgt daraus, dass der y-Wert 0 sein muss.
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu berechnen, muss der x-Wert gleich 0 sein.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Quadratische Ergänzung
Um den Scheitelpunkt aus der Scheitelform zu bestimmen, muss eine quadratische Ergänzung mit dem Funktionsterm durchgeführt werden.
↓ 4 ausklammern. Distributivgesetz.
↓ ↓ In eine Binomische Formel umschreiben.
↓ Distributivgesetz. anwenden.
Scheitelpunkt:
Nullstellen berechnen
Das Berechnen der Nullstellen funktioniert für quadratische Funktionen allgemein immer mit der Mitternachtsformel.
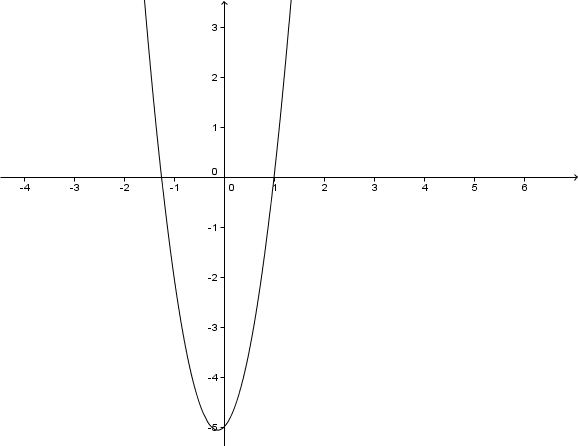
Setze . Mitternachtsformel anwenden. Dafür die Diskriminante D berechnen.
2 Lösungen
Mitternachtsformel anwenden.
Schnittpunkt mit der x-Achse
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu berechnen, muss der x-Wert gleich 0 sein.
Hast du eine Frage oder Feedback?
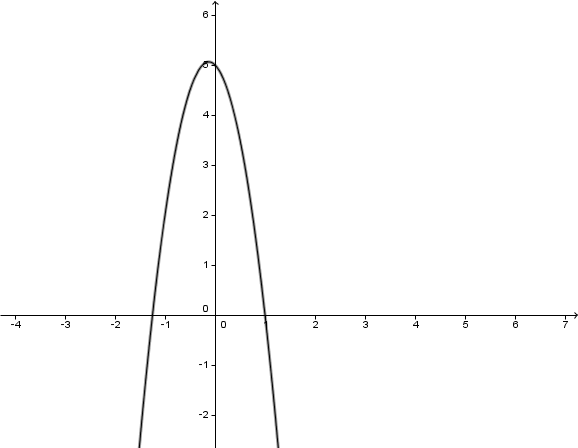
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Quadratische Ergänzung
Um den Scheitelpunkt aus der Scheitelform zu bestimmen, muss eine quadratische Ergänzung mit dem Funktionsterm durchgeführt werden.
↓ -4 ausklammern. Distributivgesetz.
↓ ↓ In eine Binomische Formel umschreiben.
↓ Zusammenfassen
↓ Distributivgesetz. anwenden.
Scheitelpunkt:
Nullstellen berechnen
Das Berechnen der Nullstellen funktioniert für quadratische Funktionen allgemein immer mit der Mitternachtsformel.
Setze . Mitternachtsformel anwenden. Dafür die Diskriminante D berechnen.
2 Lösungen
Mitternachtsformel anwenden.
Schnittpunkt mit der x-Achse
Wenn man die Nullstellen berechnet hat, folgt daraus, dass der y-Wert 0 sein muss.
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu berechnen, muss der x-Wert gleich 0 sein.
Hast du eine Frage oder Feedback?
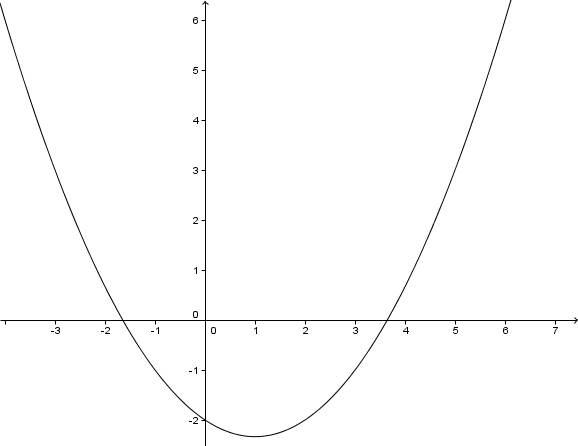
Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadratische Funktionen
Quadratische Ergänzung
Um den Scheitelpunkt aus der Scheitelform zu bestimmen, muss eine quadratische Ergänzung mit dem Funktionsterm durchgeführt werden.
↓ ausklammern. Distributivgesetz.
↓ Zusammenfassen
↓ ↓ In eine Binomische Formel umschreiben.
↓ Zusammenfassen
↓ Ausmultiplizieren
Scheitelpunkt:
Nullstellen berechnen
Das Berechnen der Nullstellen funktioniert für quadratische Funktionen allgemein immer mit der Mitternachtsformel.
Setze . Mitternachtsformel anwenden. Dafür die Diskriminante D berechnen.
↓ Gemeinsamen Hauptnenner bilden und auf diesen erweitern.
2 Lösungen, die sich nach Formel ergeben zu:
Schnittpunkt mit der x-Achse
Wenn man die Nullstellen berechnet hat, folgt daraus, dass der y-Wert 0 sein muss.
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der y-Achse zu berechnen, muss der x-Wert gleich 0 sein.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?
