Wahlteil - lernen mit Serlo!

Analysis A1.1

Für jedes $k > 0$ ist eine Funktion $f_{k}$ festgelegt durch

f_{k} (x) = \frac{e^{k x} + e^{- k x}}{2 k}; x \in ℝ

Ihr Schaubild sei $C_{k}$ .

a) Skizzieren Sie für $k = 0,5, k = 1$ und $k = 2$ die Schaubilder $C_{k}$ in ein gemeinsames Koordinatensystem.

Zeigen Sie, dass $C_{1}$ achsensymmetrisch zur y-Achse ist.

Bestimmen Sie den Tiefpunkt von $C_{1}$ .

b) Das Schaubild $C_{k}$ schließt mit der $x$ -Achse und den Geraden $x = 0$ und $x = 1 / k$ eine Fläche ein. Bestimmen Sie den Inhalt dieser Fläche.

Eine Hängebrücke in einem Klettergarten wird durch die untere Skizze dargestellt.

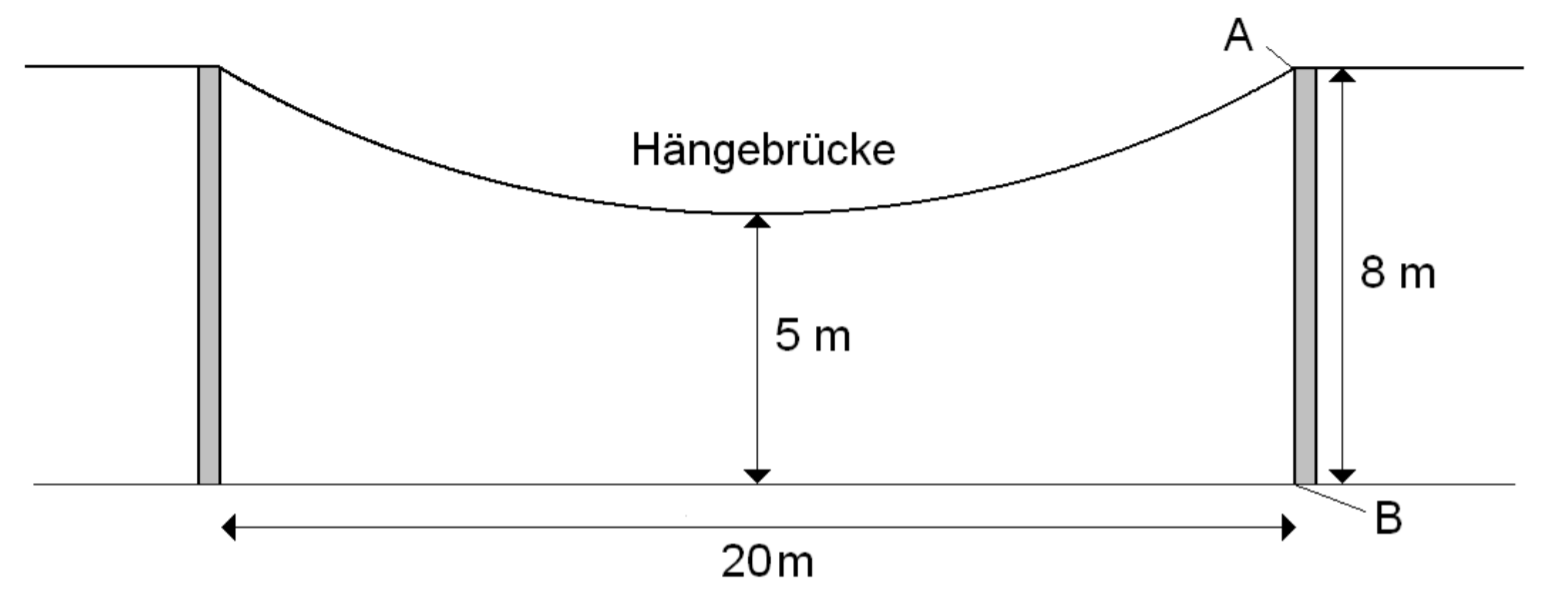
c) Das Profil der Brücke soll durch den Graphen der Funktion $g (x) = a \cdot \frac{e^{k x} + e^{- k x}}{2 k}$ ( $x$ und $y$ in $m$ ) beschrieben werden. Bestimmen Sie $a$ und $k$ .

d) Bestimmen Sie unter welchem Winkel die Brücke im Punkt $A$ auf die waagrechte Plattform trifft.

e) Zur Stabilisierung der Brücke wird im Punkt $B$ ein Halteseil am Boden befestigt und senkrecht im Punkt $P$ an die Brücke angebracht. Bestimmen Sie die Koordinaten des Befestigungspunktes $P$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion

Lösung zu a)

Zum Schaubild $C_{1}$ gehört die Funktion $f_{1} (x) = \frac{1}{2} \cdot (e^{x} + e^{- x})$ .

Bei Achsensymmetrie zur $y$ -Achse gilt: $f_{1} (- x) = f_{1} (x)$

$\Rightarrow f_{1} (- x) = \frac{1}{2} \cdot (e^{- x} + e^{- (- x})) = \frac{1}{2} \cdot (e^{- x} + e^{x}) = f_{1} (x) ✓$

Antwort: $C_{1}$ ist achsensymmetrisch zur y-Achse.

Im Tiefpunkt von $C_{1}$ gilt: $f_{1}^{'} (x) = 0$

$f_{1}^{'} (x)$	$=$	$0$
$\frac{1}{2} \cdot (e^{x} - e^{- x})$	$=$	$0$	$\cdot 2$
$e^{x} - e^{- x}$	$=$	$0$	$\cdot e^{x}$
	↓	Beseitige den negativen Exponenten.
$e^{2 x} - 1$	$=$	$0$	$+ 1$
	↓	Löse nach $x$ auf.
$e^{2 x}$	$=$	$1$	$\ln$
$2 x$	$=$	$\ln (1)$
$2 x$	$=$	$0$	$: 2$
$x$	$=$	$0$

An der Stelle $x = 0$ liegt ein Extremum vor. Da im Aufgabentext von einem Tiefpunkt die Rede ist, muss die hinreichende Bedingung nicht überprüft werden.

Berechne $f (0)$ : $f (0) = \frac{1}{2} \cdot (e^{0} + e^{- 0}) = \frac{1}{2} \cdot 2 = 1$

Antwort: Der Tiefpunkt hat die Koordinaten $T P (0 | 1)$ .

Lösung zu b)

$A_{k} = \int_{0}^{\frac{1}{k}} \frac{1}{2 k} \cdot (e^{k x} + e^{- k x}) d x$

$= \frac{1}{2 k} \cdot {[\frac{e^{k x}}{k} - \frac{e^{- k x}}{k}]}_{0}^{\frac{1}{k}}$

$= \frac{1}{2 k^{2}} \cdot {[e^{k x} - e^{- k x}]}_{0}^{\frac{1}{k}}$

$= \frac{1}{2 k^{2}} \cdot [(e^{1} - e^{- 1}) - (1 - 1)]$

$= \frac{1}{2 k^{2}} \cdot (e^{1} - e^{- 1})$

Antwort: Der Inhalt der eingeschlossenen Fläche beträgt $A_{k} = \frac{1}{2 k^{2}} \cdot (e^{1} - e^{- 1})$ .

Lösung zu c)

Lege das Koordinatensystem symmetrisch zur Hängebrücke, d.h. die $x$ -Achse ist der Boden und die $y$ -Achse geht durch die Brückenmitte.

Gegeben ist die Funktion $g (x) = a \cdot \frac{e^{k x} + e^{- k x}}{2 k}$

Da die Hängebrücke für $x = 0$ eine Höhe von $5 m$ hat, gilt $g (0) = 5$

$\Rightarrow g (0) = a \cdot \frac{e^{k \cdot 0} + e^{- k \cdot 0}}{2 k} = a \cdot \frac{1 + 1}{2 k} = a \cdot \frac{2}{2 k} = \frac{a}{k} = 5$

Andererseits gilt $g (10) = 8$

$\Rightarrow \frac{}{} a \cdot \frac{e^{k \cdot 10} + e^{- k \cdot 10}}{2 k} = 8$

$\Rightarrow \frac{a}{k} \cdot \frac{e^{k \cdot 10} + e^{- k \cdot 10}}{2} = 8$

$\Rightarrow \frac{a}{k} \cdot (e^{k \cdot 10} + e^{- k \cdot 10}) = 16$

Mit $\frac{a}{k} = 5$ folgt dann: $5 \cdot (e^{k \cdot 10} + e^{- k \cdot 10}) = 16$ bzw. $e^{k \cdot 10} + e^{- k \cdot 10} = \frac{16}{5}$

$e^{10 \cdot k} + e^{- 10 \cdot k}$	$=$	$\frac{16}{5}$	$\cdot e^{10 \cdot k}$
	↓	Beseitige den negativen Exponenten.
$e^{20 \cdot k} + 1$	$=$	$\frac{16}{5} \cdot e^{10 \cdot k}$	$- \frac{16}{5} \cdot e^{10 \cdot k}$
	↓	Bringe die Terme auf eine Seite.
$e^{20 \cdot k} - \frac{16}{5} \cdot e^{10 \cdot k} + 1$	$=$	$0$
	↓	Setze $z = e^{10 \cdot k}$ .
$z^{2} - \frac{16}{5} z + 1$	$=$	$0$

Du hast eine quadratische Gleichung erhalten. Diese kannst du mit der Mitternachtsformel (abc-Formel) oder mit der pq-Formel lösen. Hier erfolgt die Lösung mit der pq-Formel.

Lies dazu die Werte von p und q ab: $p = - \frac{16}{5}$ und $q = 1$

$z_{1,2}$	$=$	$- \frac{p}{2} \pm \sqrt{{(\frac{p}{2})}^{2} - q}$
	↓	Setze $p = - \frac{16}{5}$ und $q = 1$ ein.
	$=$	$- \frac{(- \frac{16}{5})}{2} \pm \sqrt{{(\frac{- \frac{16}{5}}{2})}^{2} - 1}$
	↓	Vereinfache.
	$=$	$\frac{8}{5} \pm \sqrt{{(\frac{8}{5})}^{2} - 1}$
	$=$	$\frac{8}{5} \pm \sqrt{\frac{64}{25} - 1}$
	$=$	$\frac{8}{5} \pm \sqrt{\frac{39}{25}}$
	$=$	$\frac{8 \pm \sqrt{39}}{5}$
$z_{1}$	$=$	$\frac{8 - \sqrt{39}}{5}$
$z_{1}$	$\approx$	$0,351$
$z_{2}$	$=$	$\frac{8 + \sqrt{39}}{5}$
$z_{2}$	$\approx$	$2,849$

Rücksubstitution ergibt: $0,351 = e^{10 k}$ $\Rightarrow k_{1} = 0,1 \cdot \ln (0,351) \approx - 0,105$

Die Lösung $k_{1} = - 0,105$ entfällt, da $k$ laut Aufgabenstellung $> 0$ sein soll.

Damit folgt aus der zweiten Lösung $2,849 = e^{10 k} \Rightarrow k = 0,1 \cdot \ln (2,849) \approx 0,105$

Mit der am Anfang ermittelten Beziehung $\frac{a}{k} = 5 \Rightarrow a = 5 \cdot k \Rightarrow a = 5 \cdot 0,105 = 0,525$

Antwort: Die gesuchten Parameter lauten $k = 0,105$ und $a = 0,525$ .

Lösung zu d)

Der Punkt $A$ hat die Koordinaten $A (10 | 8)$ .

Die Funktion $g (x)$ lautet:

$g (x) = \frac{0,525}{2 \cdot 0,105} \cdot (e^{0,105 \cdot x} + e^{- 0,105 \cdot x}) = 2,5 \cdot (e^{0,105 \cdot x} + e^{- 0,105 \cdot x})$

Berechne die Ableitung, beachte dabei die Kettenregel:

$g^{'} (x) = 2,5 \cdot 0,105 \cdot (e^{0,105 \cdot x} - e^{- 0,105 \cdot x})$

$g^{'} (x) = 0,2625 \cdot (e^{0,105 \cdot x} - e^{- 0,105 \cdot x})$

An der Stelle $x = 10$ erhältst du für die Ableitung:

$g^{'} (10) = 0,2625 \cdot (e^{0,105 \cdot 10} - e^{- 0,105 \cdot 10}) = 0,2625 \cdot (e^{1,05} - e^{- 1,05}) \approx 0,658$

Um den Winkel zu berechnen, setze $\tan (α) = g^{'} (10) = 0,658 \Rightarrow α \approx {33,3}^{\circ}$

Antwort: Die Brücke trifft unter einem Winkel von etwa ${33,3}^{\circ}$ im Punkt $A$ auf die waagrechte Plattform.

Lösung zu e)

Gesucht ist zunächst die Gleichung der Normalen vom Punkt $B (10 | 0)$ an den Graphen von $g (x)$ .

Allgemein lautet die Normalengleichung im Punkt $P (x_{0} | g (x_{0})$ :

$n (x) = - \frac{1}{g^{'} (x_{0})} \cdot (x - x_{0}) + g (x_{0})$

Setze $g^{'} (x_{0})$ in $n (x)$ ein:

$\Rightarrow n (x) = - \frac{1}{0,2625 \cdot (e^{0,105 \cdot x_{0}} - e^{- 0,105 \cdot x_{0}})} \cdot (x - x_{0}) + g (x_{0})$

$\Rightarrow n (x) = - \frac{1}{0,2625 \cdot (e^{0,105 \cdot x_{0}} - e^{- 0,105 \cdot x_{0}})} \cdot (x - x_{0}) + 2,5 \cdot (e^{0,105 \cdot x_{0}} + e^{- 0,105 \cdot x_{0}})$

Der Punkt $B (10 | 0)$ muss die Normalengleichung erfüllen. $B$ eingesetzt ergibt die folgende Gleichung:

$0 = - \frac{1}{0,2625 \cdot (e^{0,105 \cdot x_{0}} - e^{- 0,105 \cdot x_{0}})} \cdot (10 - x_{0}) + 2,5 \cdot (e^{0,105 \cdot x_{0}} + e^{- 0,105 \cdot x_{0}})$

Umgeformt erhältst du:

$10 - x_{0} = 2,5 \cdot (e^{0,105 \cdot x_{0}} + e^{- 0,105 \cdot x_{0}}) \cdot 0,2625 \cdot (e^{0,105 \cdot x_{0}} - e^{- 0,105 \cdot x_{0}})$

Beachte die $3$ . binomische Formel:

$10 - x_{0} = 0,65625 \cdot (e^{0,21 \cdot x_{0}} - e^{- 0,21 \cdot x_{0}})$

Die Gleichung kannst du mit der SOLVE - Funktion deines Taschenrechners lösen.

Du erhältst: $x_{0} \approx 7,18$

Eingesetzt in $g (x)$ folgt: $g (7,18) = 2,5 \cdot (e^{0,105 \cdot 7,18} + e^{- 0,105 \cdot 7,18}) \approx 6,49$

Antwort: Der Befestigungspunkt $P$ hat die Koordinaten $P (7,18 | 6,49)$ .

Dieses Werk steht unter der freien Lizenz
CC BY 4.0 mit Namensnennung Landesbildungsserver Baden-Württemberg → Was bedeutet das?