Wahlteil
- 1
Analysis A1.1
Für jedes ist eine Funktion festgelegt durch
Ihr Schaubild sei .
a) Skizzieren Sie für und die Schaubilder in ein gemeinsames Koordinatensystem.
Zeigen Sie, dass achsensymmetrisch zur y-Achse ist.
Bestimmen Sie den Tiefpunkt von .
b) Das Schaubild schließt mit der -Achse und den Geraden und eine Fläche ein. Bestimmen Sie den Inhalt dieser Fläche.
Eine Hängebrücke in einem Klettergarten wird durch die untere Skizze dargestellt.
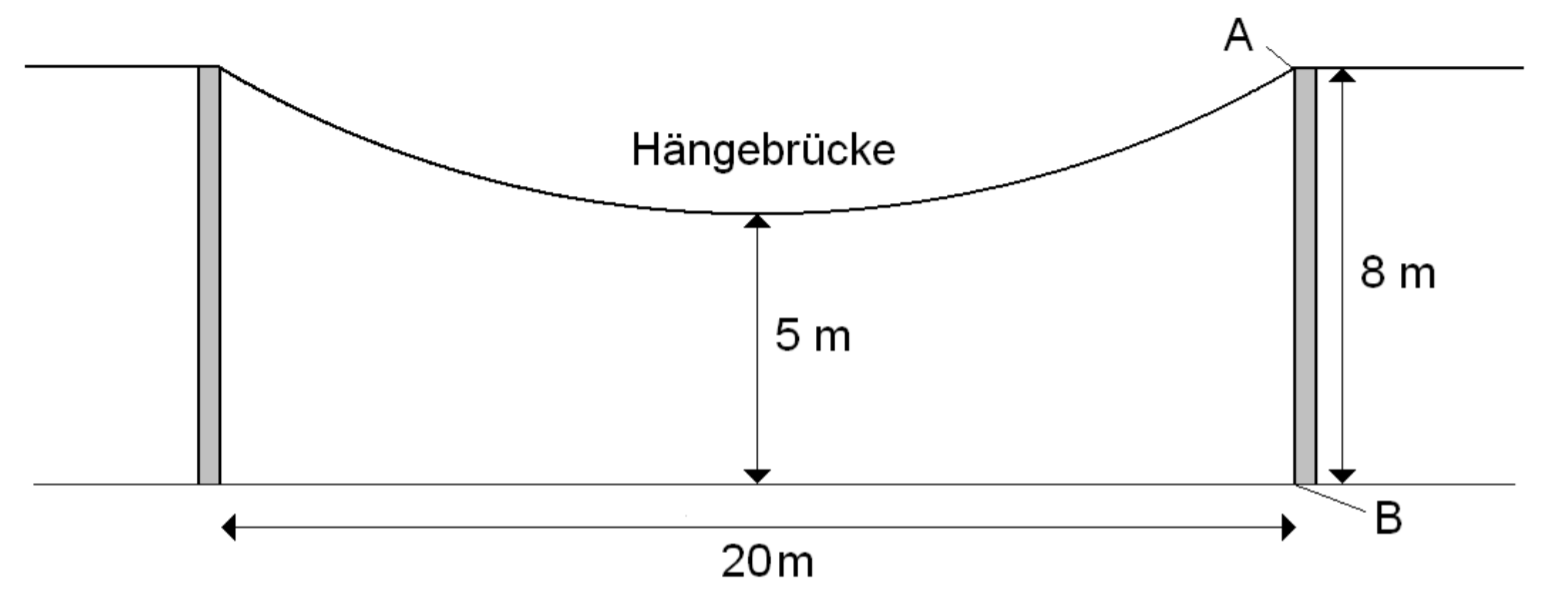
c) Das Profil der Brücke soll durch den Graphen der Funktion ( und in ) beschrieben werden. Bestimmen Sie und .
d) Bestimmen Sie unter welchem Winkel die Brücke im Punkt auf die waagrechte Plattform trifft.
e) Zur Stabilisierung der Brücke wird im Punkt ein Halteseil am Boden befestigt und senkrecht im Punkt an die Brücke angebracht. Bestimmen Sie die Koordinaten des Befestigungspunktes .
- 2
Analysis A1.2
Ein Kegel mit dem Radius und der Höhe entsteht, indem das Schaubild einer Funktion um die -Achse rotiert.
Bestimmen Sie die Funktionsgleichung von .
Berechnen Sie das Volumen des Kegels mithilfe eines geeigneten Integrals und weisen Sie so die Richtigkeit der Formel nach.
- 3
Analytische Geometrie B1
Ein rechteckiger Spiegel hat die Eckpunkte , und . Er lässt sich um die Strecke durch die Punkte und drehen.
Weiterhin ist für jedes eine Ebene durch die Gleichung gegeben. Für jedes wird durch die Ebene eine mögliche Lage des Spiegels dargestellt.
a) Zeichnen Sie den Spiegel und die Strecke in ein Koordinatensystem.
Zeigen Sie, dass der Spiegel in der Ebene liegt.
Zeichnen Sie die Ebene ein.
Der Spiegel dreht sich nun so, dass er in der Ebene liegt. Berechnen Sie, um wieviel Grad er sich dabei gedreht hat.
Beschreiben Sie, wie sich die Stellung des Spiegels in Abhängigkeit von ändert.
Bestimmen Sie, welche Stellung des Spiegels durch keine Ebene dargestellt wird.
b) Bestimmen Sie die Koordinaten der Eckpunkte des Spiegels, wenn der Spiegel in der Ebene liegt und zeichnen Sie den Spiegel für diese Lage ein.
c) Im Punkt befindet sich eine Lichtquelle, welche einen Lichtstrahl in Richtung aussendet.
Zeigen Sie, dass der Lichtstrahl den Spiegel unabhängig von dessen Stellung immer im gleichen Punkt trifft.
- 4
Stochastik C1
Der Body-Mass-Index ist eine Maßzahl für die Bewertung des Körpergewichts eines Menschen in Relation zu seiner Körpergröße.
Menschen mit einem BMI > 25 gelten laut diesem Index bereits als übergewichtig.
a) Laut statistischem Bundesamt waren im Jahr 2017 60 % der männlichen Bevölkerung übergewichtig (BMI >25).
Berechnen Sie, die Wahrscheinlichkeit folgender Ereignisse:
A: „Unter 10 zufällig ausgewählten Männern sind genau 6 Männer übergewichtig.“
B: „Unter 10 zufällig ausgewählten Männern sind mehr als die Hälfte übergewichtig.“
C: „Unter 10 zufällig ausgewählten Männern sind nur die ersten drei nicht übergewichtig.“
b) Wie hoch müsste der Anteil der Übergewichtigen in der weiblichen Bevölkerung mindestens sein, damit mit einer Wahrscheinlichkeit von mindestens 95 % unter 100 zufällig ausgewählten Frauen mindestens 50 Übergewichtige sind.
c) In der Gesamtbevölkerung Deutschlands betrug der Anteil der Übergewichtigen im Jahr 2017 laut statistischem Bundesamt 54 %.
Ein Dorf hat 500 Einwohner. Bestimmen Sie ein Intervall, in dem die Anzahl der Übergewichtigen in dem Dorf mit 95 %-iger Sicherheit liegen wird.
Ein Sportverein in dem Dorf hat 90 Mitglieder. Der Vereinsvorsitzende behauptet, dass der Anteil der Übergewichtigen in seinem Verein geringer als in der sonstigen Bevölkerung ist.
Um dies zu überprüfen, wird die Nullhypothese auf dem Signifikanzniveau 10 % getestet und das BMI der 90 Mitglieder ermittelt.
Bestimmen Sie die zugehörige Entscheidungsregel.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?





