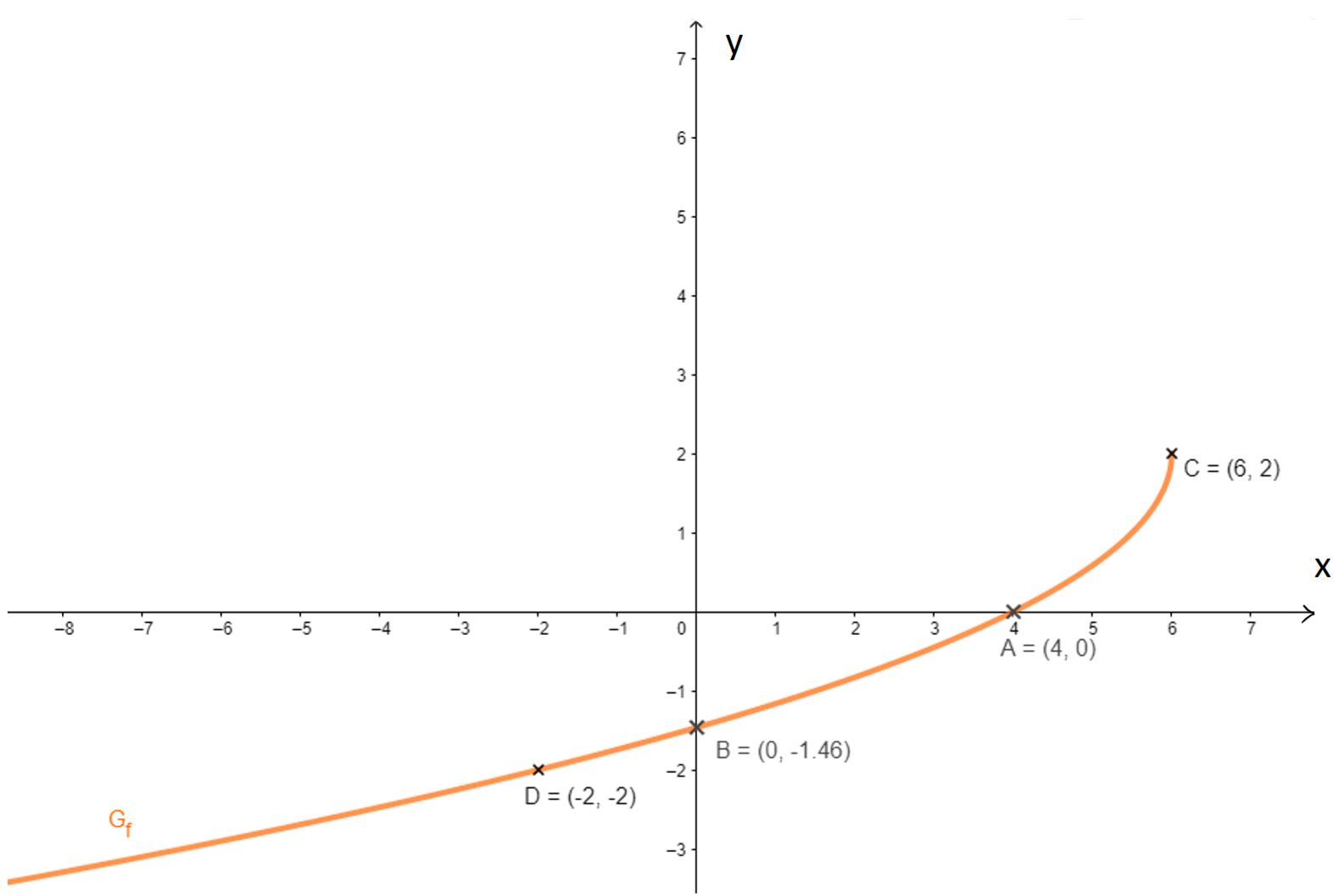
Gegeben ist die Funktion mit maximaler Definitionsmenge . Der Graph von wird mit bezeichnet.
Berechnen Sie die Koordinaten der Schnittpunkte von mit den Koordinatenachsen. Bestimmen Sie das Verhalten von für und geben Sie an. (5BE)
Bestimmen Sie den Term der Ableitungsfunktion von und geben Sie die maximale Definitionsmenge von an.Bestimmen Sie und beschreiben Sie, welche Eigenschaften von aus diesem Ergebnis folgt. (zur Kontrolle: ) (5BE)
Geben Sie das Monotonieverhalten von und die Wertemenge von an. (2BE)
Geben Sie an und zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse in ein Koordinatensystem ein (Platzbedarf im Hinblick auf die folgenden Aufgaben: ). (3BE)
Die Funktion ist in umkehrbar. Geben Sie die Definitionsmenge der Umkehrfunktion von an und zeigen Sie, dass gilt. (4BE)