Eine Wahrscheinlichkeitsverteilung ist eine Funktion, die den Ergebnissen eines Zufallsexperimentes ihre Wahrscheinlichkeiten zuordnet.
Jede Wahrscheinlichkeitsverteilung erfüllt die drei Axiome von Kolmogorow:
Bei endlichen Zufallsvariablen gibt man die Wahrscheinlichkeitsverteilung oft in tabellarischer Form an.
Manchmal wird die Wahrscheinlichkeitsverteilung auch Wahrscheinlichkeitsmaß oder Wahrscheinlichkeitsgesetz genannt.
Beispiele, bei denen man die Zuordnung mit festen Formel ermitteln kann:
Binomialverteilung (diskrete Verteilung)
Normalverteilung (stetige Verteilung)
Hypergeometrische Verteilung (diskrete Verteilung)
Poissonverteilung (diskrete Verteilung)
Diskrete Verteilungen sind Verteilungen auf diskreten, also abzählbaren Zufallsgrößen.
Stetige Verteilungen sind Verteilungen auf reellen Zahlen.
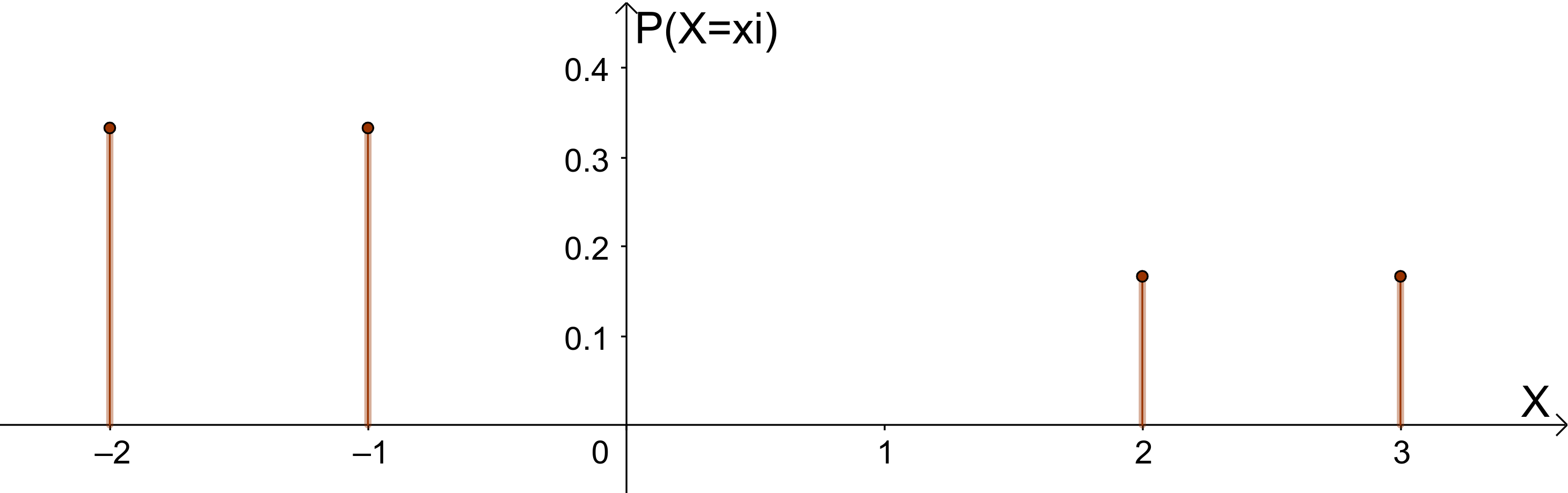
Stabdiagramm einer Wahrscheinlichkeitsverteilung
Beispiel
Folgendes Spiel wird angeboten: Nachdem man 2€ Einsatz gezahlt hat, darf man einmal würfeln. Fällt eine Sechs, bekommt man 5€ ausgezahlt. Fällt eine 2, bekommt man 4€ ausgezahlt. Bei den Zahlen 1 und 3 bekommt man 1€ ausgezahlt. X sei der Gewinn in diesem Spiel.
Um auf die Werte von X zu kommen, musst du von den Auszahlungen den Einsatz abziehen.
Fällt eine 4 oder 5, hat man zwei Euro verloren, bei einer 1 oder 3 hat man einen Euro verloren. Bei einer 2 gewinnt man zwei Euro, bei einer 6 sogar drei Euro.
Wahrscheinlichkeitsverteilung
-2 | -1 | 2 | 3 | |
|---|---|---|---|---|
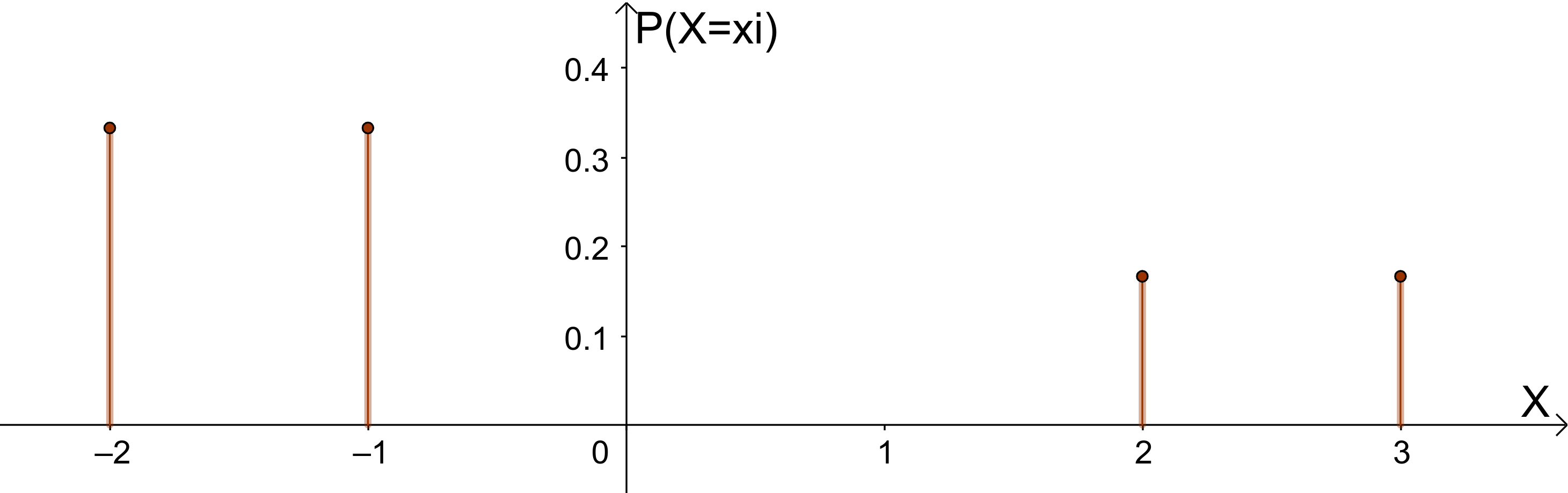
Stabdiagramm der Wahrscheinlichkeitsverteilung
Beispiel
Folgendes Zufallsexperiment soll untersucht werden: Eine Münze wird dreimal geworfen. Es soll geprüft werden, wie oft sich das vorangegangene Ergebnis wiederholt.
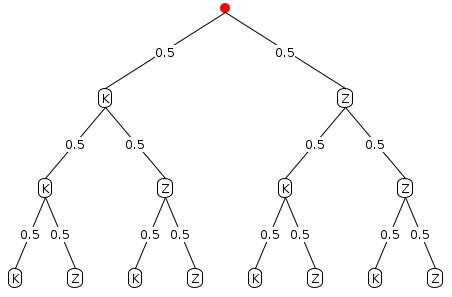
Baumdiagramm zum dreimaligen Münzwurf
Im ganz linken Pfad wird zwei mal Kopf wiederholt. Im ganz rechten wird zweimal Zahl wiederholt. Beim zweiten, vierten, fünften und siebten Pfad wird einmal ein Ergebnis wiederholt. Bei den restlichen wird nichts wiederholt.
Wahrscheinlichkeitsverteilung
0 | 1 | 2 | |
|---|---|---|---|
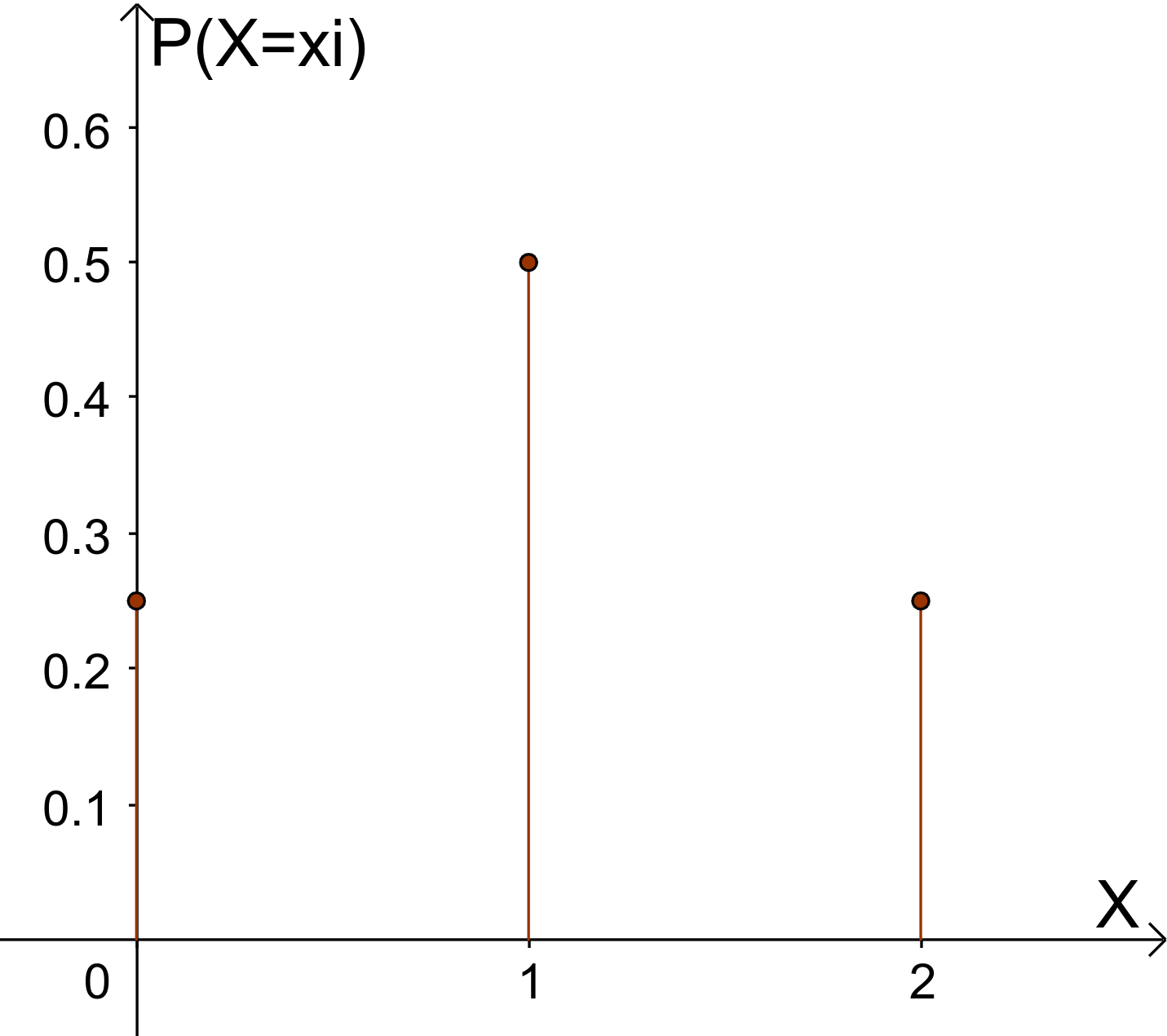
Stabdiagramm der Wahrscheinlichkeitsverteilung
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Zufallsgrößen und Verteilungsfunktion
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
