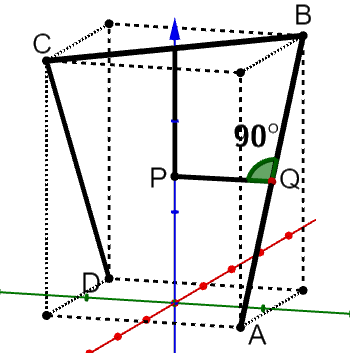
Aufgabe 3A
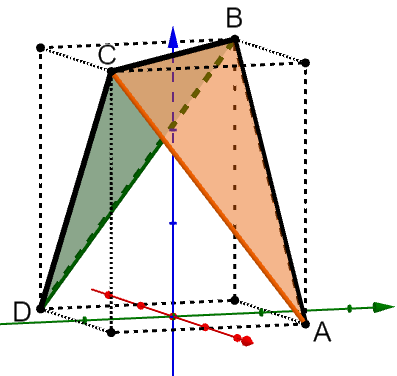
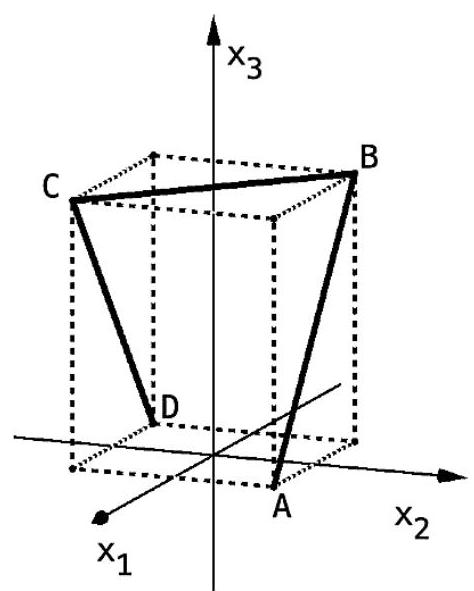
Die Abbildung zeigt das sogenannte Saarpolygon, ein im Inneren begehbares Denkmal zur Erinnerung an den stillgelegten Kohlebergbau im Saarland. Das Saarpolygon kann in einem Koordinatensystem modellhaft durch den Streckenzug dargestellt werden, der aus den drei Strecken und mit
und besteht. und sind Eckpunkte eines Quaders.
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.

Begründen Sie, dass die Punkte und symmetrisch bezüglich der -Achse liegen. (2 BE)
Berechnen Sie die Länge des Streckenzugs in der Wirklichkeit. (3 BE)
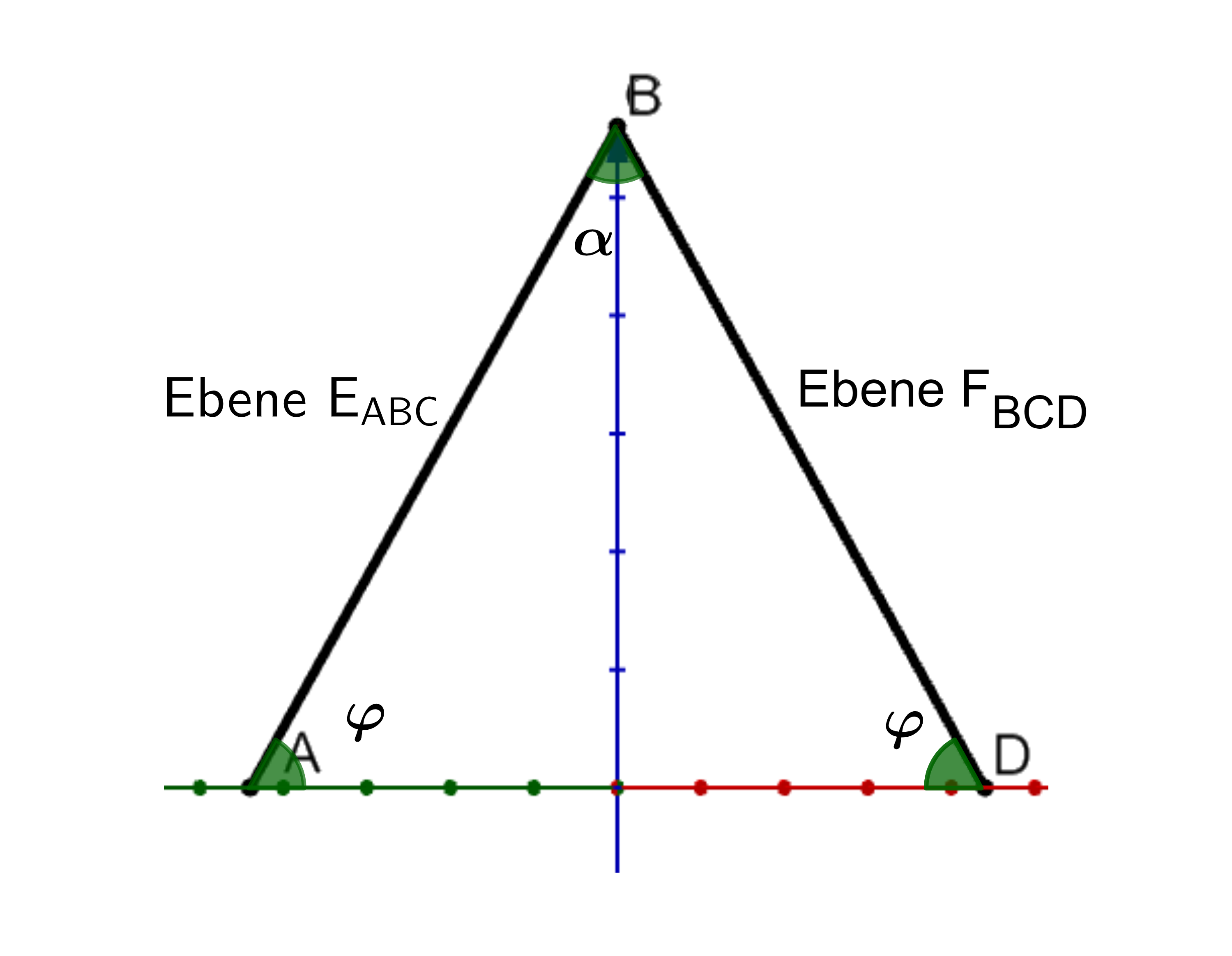
Die Ebene enthält die Punkte und , die Ebene enthält die Punkte und .
Bestimmen Sie eine Gleichung von in Koordinatenform. (3 BE)
[Zur Kontrolle: ]
Berechnen Sie die Größe des Winkels, unter dem die -Ebene schneidet.
Geben Sie einen Term an, mit dem aus die Größe des Winkels zwischen den Ebenen und berechnet werden kann. (5 BE)
Die Ebene teilt den Quader in zwei Teilkörper.
Bestimmen Sie das Verhältnis der Volumina der beiden Teilkörper. (4 BE)
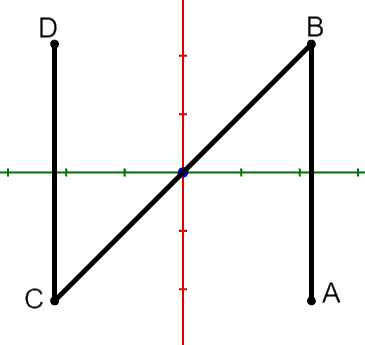
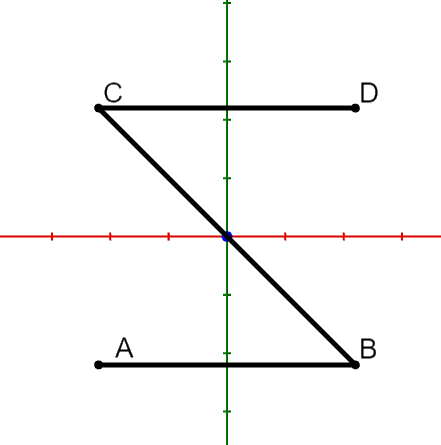
Das Saarpolygon wird von verschiedenen Positionen aus betrachtet. Die Abbildungen 1 und 2 stellen das Saarpolygon für zwei dieser Positionen schematisch dar.

Abbildung 1
Geben Sie zu jeder der beiden Abbildungen einen möglichen Vektor an, der die zu der Position gehörige Blickrichtung beschreibt.
Stellen Sie das Saarpolygon schematisch für eine Betrachtung von oben dar. (4 BE)
Abbildung 2
Der Punkt liegt innerhalb des Quaders und hat von den drei Strecken und den gleichen Abstand. Das folgende Gleichungssystem liefert den Wert von :
i.
ii.
iii.
Erläutern Sie die Überlegungen, die diesem Vorgehen zur Bestimmung des Wertes von zugrunde liegen. (4 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?