1 Quadratwurzeln
In diesem Kurs geht es um die Einführung von Quadratwurzeln und die zugehörigen Rechenregeln.
Dauer: ca. 1,5 h
Vorwissen
Du solltest wissen, was die Menge der rationalen Zahlen ist. Außerdem sind Kenntnisse rund um den Betrag hilfreich.
Du lernst:
Definition einer Quadratwurzel
Rechnen mit Quadratwurzeln
teilweises Wurzelziehen
Rationalmachen des Nenners

2 Motivation (1/2)
Karl ist absoluter Profi, wenn es darum geht, sich etwas zu merken. (Spitzname: Ein-Merk-Karl)
Heute hat er 42 quadratische Karten, mit denen er ein Memorier-Spiel spielen möchte.
Karl findet, dass er sich die Position der Karten besser merken kann, wenn in jeder Reihe und Spalte gleich viele Karten liegen, wie das zum Beispiel in der Abbildung rechts gezeigt wird.
Wird es Karl gelingen, die 42 Karten in Form eines Quadrats anzuordnen?

3 Motivation (2/2)
Karl fängt an, die Karten in immer größeren Quadraten anzuorden.
Dabei stellt er fest, dass das größte Quadrat, das er aus Karten legen kann, an jeder Seite Karten hat. Somit besteht das größte Karten-Quadrat aus Karten, Karten bleiben übrig.

Karls Freund, der schlaue Mathematicus, mag Karls Herangehensweise nicht. Karl probiert zu viel aus, bemängelt er.
Mathematicus hat eine bessere Strategie, bei der ihm sogar der Taschenrechner helfen kann.
Die Anzahl der Karten einer (Quadrat-)Seite bezeichnet Mathematicus mit . Da das Quadrat dann Reihen à Karten hat, benötigt er dafür insgesamt Karten.
Die Karten, die im Spiel enthalten sind, sollen zu einem Quadrat mit Karten gelegt werden. Daher stellt Mathematicus die Gleichung auf.
Diese Gleichung möchte er nach auflösen. Die Definition auf der nächsten Seite hilft ihm dabei.
4 Definition
Die Quadratwurzel ist diejenige nicht negative Zahl, deren Quadrat ergibt. Dabei muss eine nicht negative Zahl sein.
„Nicht negativ“ heißt „positiv oder “.
Die Zahl unter der Wurzel heißt Radikand.
Das Berechnen der Wurzel heißt Wurzelziehen oder Radizieren.
Beispiel
Weitere Beispiele findest du auf der nächsten Seite.
5 Beispiele für Wurzeln
Wie du schon in der Definition gelernt hast, ist eine nicht negative Zahl. Im folgenden schauen wir uns ein paar Lösungen von einfachen Wurzeln an, indem wir für die Zahlen einsetzen:
Allgemein können wir also eine Wurzelgleichung der Form lösen, wenn ist. Wie sieht es aber bei einem negativen Radikanden aus?
:
Wir wählen zum Beispiel :
Wir suchen eine Zahl , für die wir wie oben schreiben können:
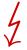
Hier kannst du allerdings kein finden, welches löst.

Wenn du eine beliebige rationale Zahl mit sich selbst multiplizierst, erhältst du immer eine positive Zahl oder . Somit gibt es keine Zahl, die du für einsetzen kannst, damit die Aussage stimmt.
6 Wurzeln und Quadrat (1/2)
Wenn du die Wurzel von einem Quadrat berechnen möchtest, kannst du einfach die Basis in Betrag setzen.
Du weißt aus der Definition, dass eine Quadratwurzel nicht negativ sein kann.
Du kannst in diesem Fall für auch negative Zahlen einsetzen, da durch das Quadrieren nur positive Zahlen oder die unter der Wurzel stehen.
Nach Definition ist das Ergebnis vom Wurzelziehen keine negative Zahl. Um das zu verhindern, verwendest du den Betrag . Durch den Betrag werden alle Zahlen, die du einsetzen kannst, positiv.
Wie du vielleicht schon bemerkt hast, haben wir diese Regel bei den vorherigen Beispielen schon angewandt.

7 Wurzeln und Quadrat (2/2)
Wenn allerdings eine Wurzel quadriert wird, sind Betragsstriche nicht notwendig:
Warum kann man hier die Betragsstriche weglassen? Zwar wäre die Lösung auch richtig, jedoch darfst du in nach Definition der Quadratwurzel nur positive rationale Zahlen einsetzen. Da du für gar keine negativen Zahlen einsetzen darfst, sind die Betragsstriche überflüssig.

8 Wurzeln: Zwei Lösungen? (1/2)
Karl und Mathematicus besuchen dieselbe Klasse. Als Hausaufgabe sollen die beiden folgende quadratische Gleichung mit Hilfe der Quadratwurzel lösen:
Am Abend unterhalten sich beide über die Hausaufgabe.
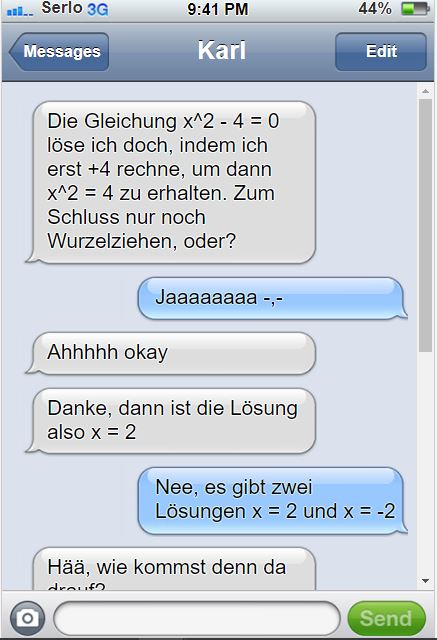
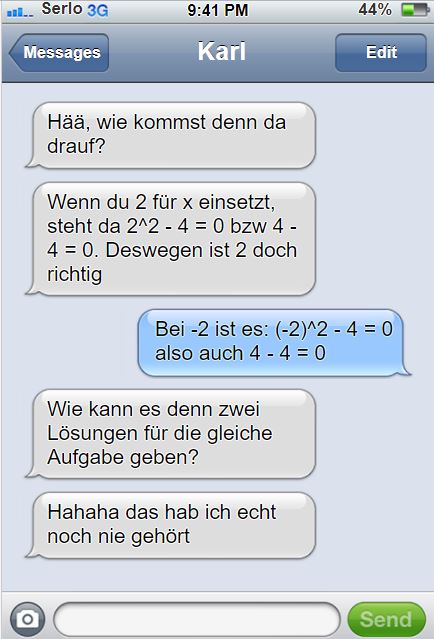
Wer von den beiden hat recht?
9 Wurzeln: Zwei Lösungen? (2/2)
Mathematicus hat recht.
Die richtige Lösung der Aufgabe ist deswegen:
Hier verwendest du die Regel, dass Betragsstriche gesetzt werden müssen, wenn der Radikand quadriert ist.
;
(alternativ: )
Bei Sachaufgaben muss man aufpassen, welche Lösungen im Sachkontext Sinn ergeben.
10 Aufgaben zur Einführung
Aufgabe 1
Laden
Aufgabe 2
Laden
11 Wurzelgesetze (1/3)
Addition und Subtraktion von Wurzeln
Addition von Wurzeln
Beispiel:
Subtraktion von Wurzeln
Beispiel:
Du siehst, dass in diesen beiden Wurzelgesetzen die Umkehrung des Distributivgesetzes benutzt wurde.
Beispiele:
12 Wurzelgesetze (2/3)
Multiplikation und Division von Wurzeln
Multiplikation von Wurzeln
Division von Wurzeln
13 Wurzelgesetze (3/3)
Bezeichnung
Allgemeine Form
Beispiel
Wurzel aus Quadrat
Quadrat einer Wurzel
Wurzel als Potenz
14 Aufgaben zu Wurzelgesetze
Aufgabe 1
Laden
Aufgabe 2
Laden
Aufgabe 3
Laden
15 Nenner rational machen
Mit Zahlen der Form kannst du besser weiterrechnen, wenn du den Bruch umformst. Dabei möchtest du erreichen, dass im Nenner keine Wurzel (also keine irrationale Zahl) steht.
Dafür erweiterst du den Bruch mit . Dadurch erhältst du:
Beispiel:
16 Aufgabe zu Nenner rational machen
Aufgabe 1
Laden
Aufgabe 2
Laden
17 Teilweises Wurzelziehen
Du weißt, dass du nicht im Kopf berechnen kannst.Jedoch gibt es eine Möglichkeit diesen Ausdruck zu vereinfachen, indem du den Radikand möglichst klein machst.
Mithilfe des Wurzelgesetzes zum Multiplizieren von Wurzeln, kannst du die Wurzel in zwei Teile teilen. Aus einem dieser Teile kannst du die Wurzel ziehen, der andere Teil bleibt unverändert.
Du kannst die Wurzel durch diese Zerlegung teilweise lösen und Rechenausdrücke sowie Terme vereinfachen.
Eine Schritt für Schritt Anleitung:
1) Zerlege den Radikanden in Primfaktoren.
2) Suche gerade Exponenten in der Zerlegung.
3) Zerlege die Wurzel in zwei Teile
Einen Teil, in dem nur gerade Exponenten vorkommen (aus denen du die Wurzel ziehen kannst).
Einen Teil, aus dem sie nicht gezogen werden kann
4) Ziehe die Wurzel bei dem ersten Teil.
5) Vereinfache den Rechenausdruck, falls möglich.
Der Term kann nicht weiter vereinfacht werden.
18 Aufgabe zum teilweisen Wurzelziehen
Laden
19 Zusammenfassung
Du weißt jetzt, was eine Quadratwurzel ist und wie du damit rechnest. Außerdem hast du gelernt, wie du Wurzeln umformen kannst, sodass du besser damit weiterrechnen kannst.
Wenn du jetzt noch wissen willst, wie du z. B. den Wert von annäherungsweise berechnen kannst, dann schau dir doch mal den Kurs Berechnung von Wurzeln an.
Interessiert dich, warum z. B. keine rationale Zahl ist und in welcher Zahlenmenge liegt, dann findest mehr dazu im Kurs Reelle Zahlen.
Möchtest du wissen, wie du die Lösung von berechnest und wie du Gleichungen mit höheren Potenzen löst, dann schau doch mal bei höheren Wurzeln vorbei.

