Mehrere lineare Gleichungen mit mehreren Unbekannten (Variablen) nennt man lineares Gleichungssystem.
Beispiel
Ein Supermarkt verkauft verschiedene Süßigkeiten. Dabei kosten 3 rote Bonbons genauso viel wie 2 grüne Lollis. 1 grüner Lolli und 3 rote Bonbons kosten zusammen 9€.
Wie viel kostet ein rotes Bonbon und ein grüner Lolli?
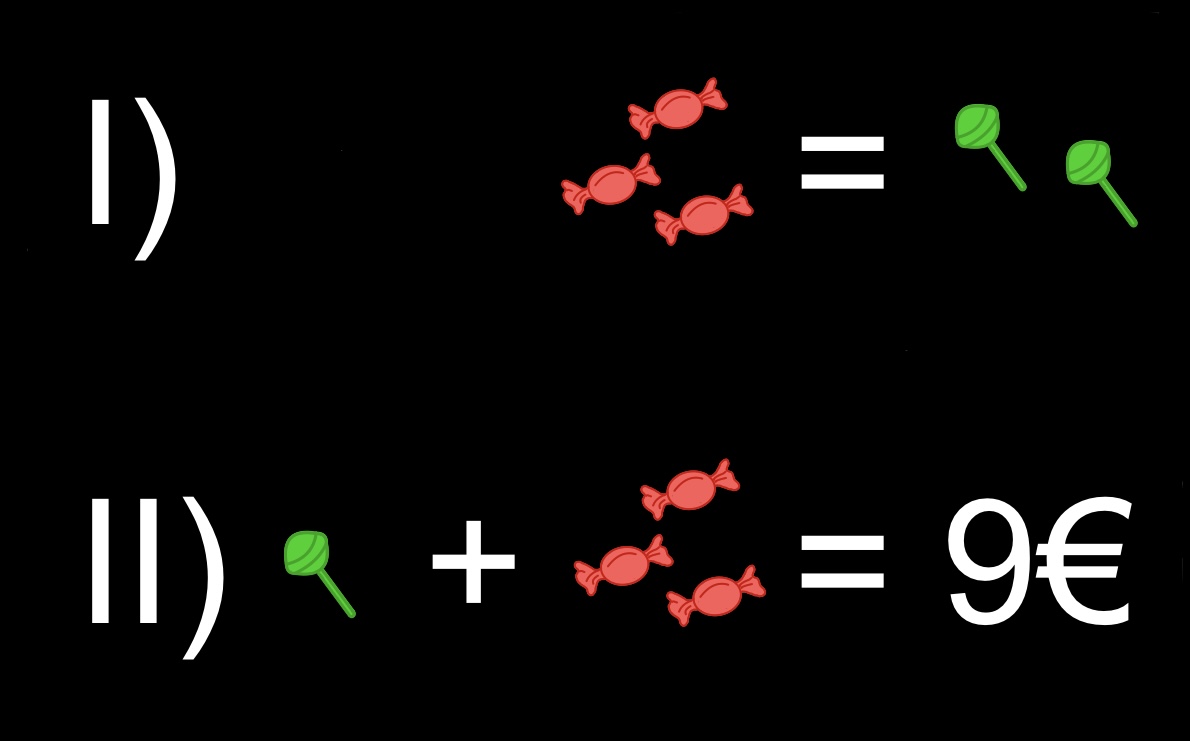
Beispiel
Wir haben schon bei linearen Gleichungen gesehen, dass die Variablen immer durch Buchstaben dargestellt werden.
Wir können also die roten Bonbons durch x ersetzen, und grünen Lollis durch y:
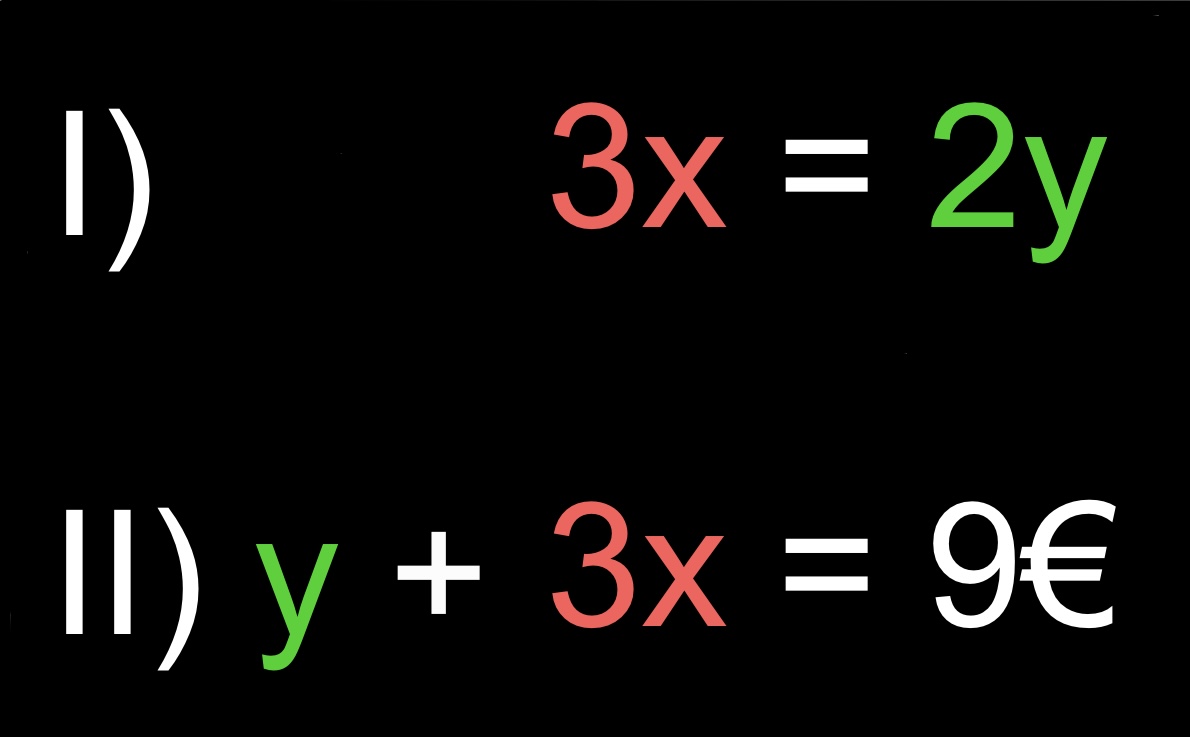
Es entsteht ein lineares Gleichungssystem
Gleichungssysteme lösen
Wie können wir nun ein lineares Gleichungssystem lösen? Das Ziel ist, für jede Variable genau einen Wert rauszubekommen. Im Beispiel oben will man herausfinden, wie viel ein rotes Bonbon und wie viel ein grüner Lolli kostet.
Es gibt verschiedene Verfahren, um ein Gleichungssystem zu lösen:
Verfahren | Anwendung |
|---|---|
Wenn man die beiden Gleichungen addieren kann, und dadurch eine Variable wegfällt | |
Wenn man leicht nach einer Variable auflösen kann | |
Wenn man zwei Gleichungen leicht nach der gleichen Variable auflösen kann |
Man kann lineare Gleichungssysteme auch graphisch lösen. Das graphische Lösen bietet sich an, wenn sich der Graph der beiden Gleichungen gut zeichnen lässt.
Detaillierte Einführung
Eine schrittweise Einführung zum Thema findest du im Kurs Einführung in lineare Gleichungssysteme - Teil 1.
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Anwendungsaufgaben zu Gleichungssystemen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
Artikel
- Additionsverfahren
- Einsetzungsverfahren
- Cramersche Regel
- Gaußverfahren
- Lösbarkeit von linearen Gleichungssystemen
