Gemischte Aufgaben zur Oberflächenberechnung

1
Berechne.
1. Eine Kugel hat die Oberfläche $O = 100 {cm}^{2}$ . Berechne den Radius $r$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Radius
  gegeben: $O = 100 π {cm}^{2}$
  gesucht: $r$
  Um den Radius zu berechnen, wenn die Oberfläche gegeben ist, benutzt du die passende Formel und forme nach $r$ um.
  $O$ $=$ $4 π r^{2}$ $: 4 π$
  $\frac{O}{4 π}$ $=$ $r^{2}$ $\sqrt{}$
  $\pm \sqrt{\frac{O}{4 π}} = r$
  Der Radius kann nur positiv sein. Du kannst also das negative Ergebnis ignorieren.
  $\sqrt{\frac{O}{4 π}} = r$
  Setze den Wert für $O$ ein.
  $r = \sqrt{\frac{100 {cm}^{2}}{4 π}}$
  Rechne mit dem Taschenrechner und runde das Ergebnis.
  $r \approx 2,821 cm$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ein Würfel hat das Volumen $V = 125 c m^{3}$ . Berechne die Oberfläche $O$ .
  cm²
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Würfel
  Gegeben: $V_{Würfel} = 125 c m^{3}$ Gesucht: $O_{Würfel}$
  Gesucht ist die Oberfläche eines Würfels. Stelle daher zunächst die Formel auf.
  $O_{Würfel} = 6 \cdot a^{2}$
  Du musst also die Seitenlänge $a$ berechnen. Diese erhältst du aus der Volumenformel:
  $V_{Würfel} = a^{3} = 125 c m^{3}$
  Daraus kannst du nun $a$ bestimmen, indem du die 3. Wurzel $\sqrt[3]{}$ ziehst. (Das bedeutet: Welche Zahl a ergibt hoch 3 genommen 125)
  $\Rightarrow a = 5 cm$ , denn $5 cm \cdot 5 cm \cdot 5 cm = 125 c m^{3}$
  Mit $a$ kannst du nun die Oberfläche berechnen.
  $O = 6 \cdot a^{2} = 6 \cdot (5 cm)^{2} = 6 \cdot 25 c m^{2} = 150 c m^{2}$
  Lösung: Die Oberfläche des Würfels ist $O = 150 c m^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Berechne die Oberfläche eines $20 cm$ hohen Zylinders mit dem Durchmesser $10 cm$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
  Gegeben: $h =$ 20 cm, $d = 2 \cdot r =$ 10 cm
  Gesucht: $O = ?$
  Stelle die Formel für die Zylinderoberfläche auf. Diese setzt sich zusammen aus der Mantelfläche $M$ und zwei Kreisflächen $A_{Kreis}$
  $O = M + 2 \cdot A_{Kreis}$
  Mantelfläche
  $M = ?$
  Stelle die Formel für die Mantelfläche auf.
  $M = U \cdot h = 2 π r \cdot h$
  Die Höhe ist gegeben als $20 cm$ . Den Radius kannst du aus dem Durchmesser berechnen. Die gegebenen Werte findest du oben. Setze diese Werte nun in die Formel ein und berechne die Mantelfläche
  $M = 2 π \cdot 5 cm \cdot 20 cm = π \cdot 200 c m^{2} \approx 628,32 c m^{2}$
  Kreisflächen
  $A = ?$
  Stelle die Formel für die Kreisfläche auf.
  $A = r^{2} \cdot π$
  Setze den Radius $r = 5 cm$ ein und berechne die Kreisfläche.
  $A = (5 cm)^{2} \cdot π = π \cdot 25 c m^{2} \approx 78,54 c m^{2}$
  Gesamte Oberfläche
  $O = M + 2 \cdot A_{Kreis}$
  Setze die eben berechneten Werte für die Mantelfläche und Kreisfläche ein und berechne die Oberfläche
  $O \approx 628,32 c m^{2} + 2 \cdot 78,54 c m^{2} = 785,4 c m^{2}$
  Lösung: Die Oberfläche des Zylinders ist $785,4 c m^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Berechne die Oberfläche der Figuren
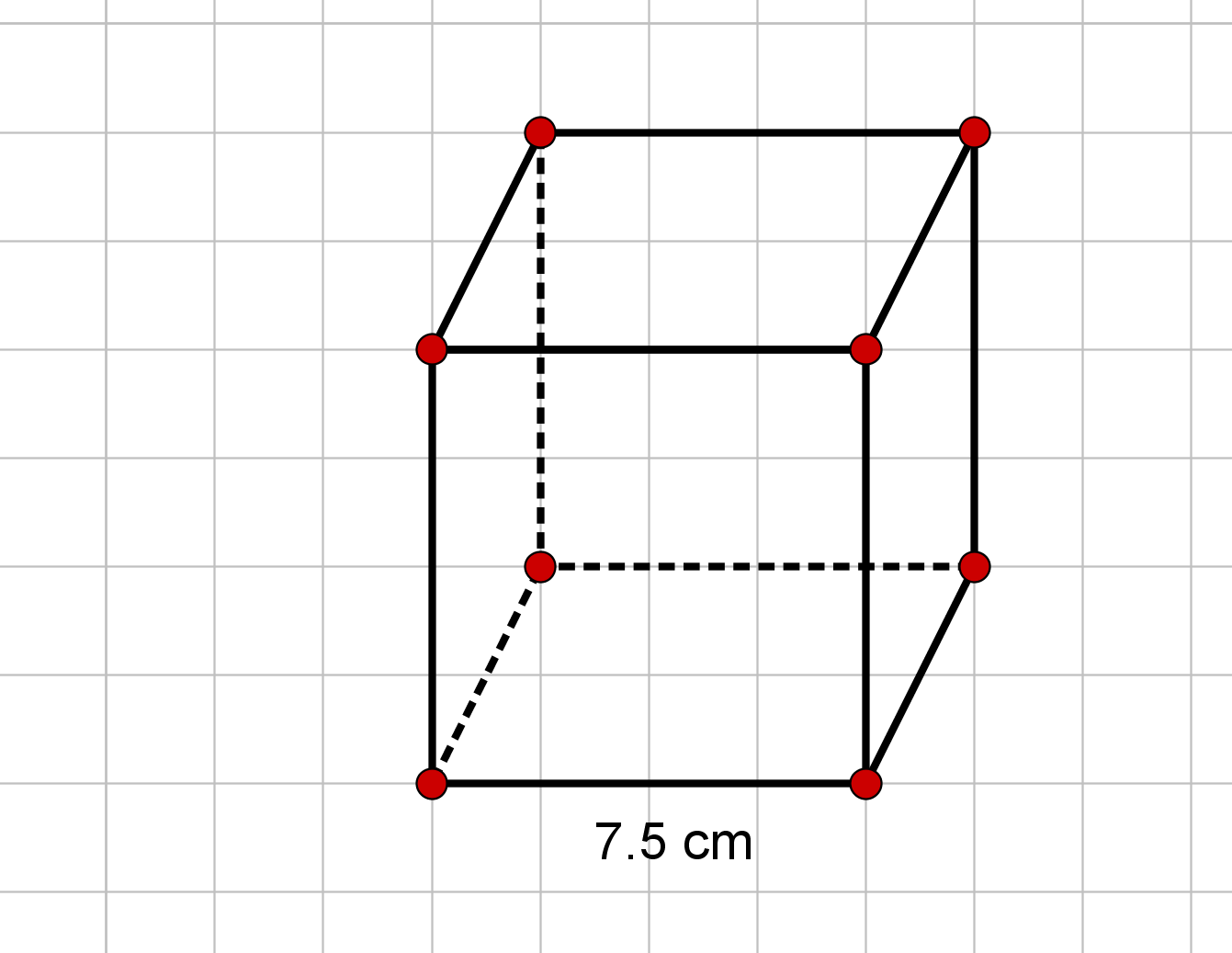1. cm²
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Oberfläche eines Würfels
  Oberfläche des Würfels
  $O = a^{2} \cdot 6$
  Setze den Wert aus dem Bild ein.
  $O = (7,5 cm)^{2} \cdot 6$
  Rechne aus.
  $O = 337,5 {cm}^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Radius $6,75 cm$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Oberfläche einer Kugel
  Oberfläche der Kugel
  $O_{K} = 4 \cdot r^{2} \cdot π$
  Setze den Wert in die Formel ein.
  $O_{k} = 4 \cdot (6,75 cm)^{2} \cdot π$
  Rechne aus
  $O_{k} = 4 \cdot 45,5625 c m^{2} \cdot π = 182,25 c m^{2} \cdot π \approx 572,56 c m^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
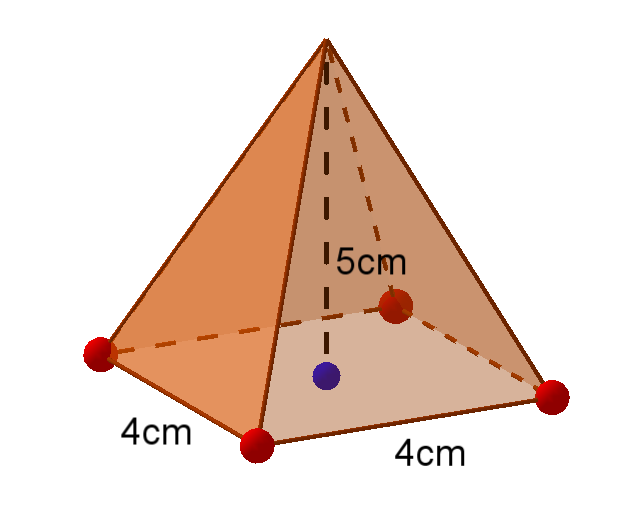
4. Für diese Aufgabe benötigst Du folgendes Grundwissen: Oberfläche einer Pyramide
  Oberfläche der Pyramide
  $O = G + M$
  Die Grundfläche G ist ein Quadrat, die Mantelfläche sind 4 Dreiecke.
  Berechne zuerst die Grundfläche
  Grundfläche: Quadrat
  Stelle die Formel für ein Quadrat auf.
  $A_{Quadrat} = a^{2}$
  Die Seitenlänge ist $4 cm$ . Setze diesen Wert in die Formel ein.
  $A_{Quadrat} = (4 cm)^{2} = 16 c m^{2}$
  Mantelfläche: Vier Dreiecke
  Höhe der Seitenflächen
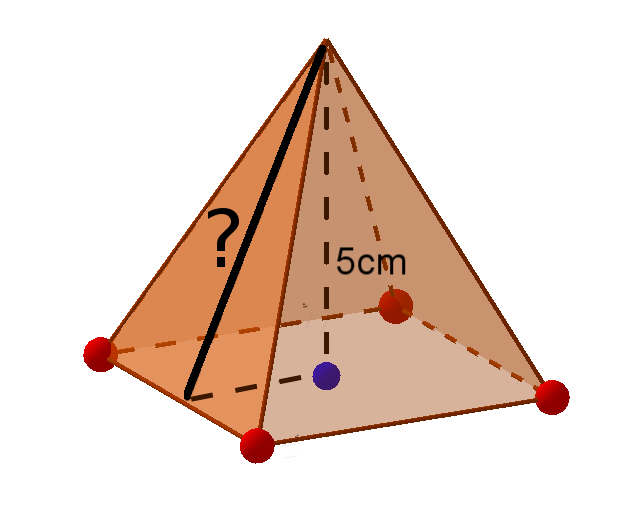
  Die Dreiecke sind alle gleich, da die Grundfläche ein Quadrat ist.
  Um die Seitenflächen zu berechnen benötigst du zuerst die Höhe der Dreiecke. Diese kannst du mit dem Satz des Pythagoras berechnen.
  $c^{2} = a^{2} + b^{2}$
  a ist die Halbe Seitenlänge des Quadrats, b ist die Höhe der Pyramide.
  $a = 4 cm : 2 = 2 cm$
  $b = 5 cm$
  Setze die Werte ein.
  $c^{2} = (2 cm)^{2} + (5 cm)^{2} = 4 c m^{2} + 25 c m^{2} = 29 c m^{2}$
  Ziehe die Wurzel um die Höhe des Dreiecks zu erhalten.
  $\Rightarrow c = \sqrt{29 c m^{2}} \approx 5,4 cm$
  Berechne damit nun die Seitenflächen.
  Seitenfläche
  Stelle die Formel für ein Dreieck auf.
  $A = \frac{1}{2} \cdot g \cdot h$
  Setze die Werte ein.
  $A = \frac{1}{2} \cdot 4 cm \cdot 5,4 cm = 10,8 c m^{2}$
  Mantelfläche
  $M = 4 \cdot A = 4 \cdot 10,8 c m^{2} = 43,2 c m^{2}$
  Oberfläche der Pyramide
  Berechne nun die Oberfläche der Pyramide, indem du Grundfläche und Mantelfläche addierst.
  $O = G + M = 16 c m^{2} + 43,2 c m^{2} = 59,2 c m^{2}$
  Lösung: Die Oberfläche der Pyramide ist $59,2 c m^{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Ein Tempel soll restauriert werden, da er ziemlich verfallen ist. Im Rahmen der Sanierungsarbeiten soll er auch einen neuen Anstrich bekommen.

Die Maße des Tempels kannst du aus dem Bild unten entnehmen.

Zusätzlich gibt dir der Bauleiter folgende Informationen:

Die Länge des Tempels ist insgesamt $90 m$ , die in drei gleich lange Teilstücke aufgeteilt sind.
Auf der Rückseite befinden sich $9$ Säulen, an jeder Breitseite jeweils $5$ und vorne insgesamt $10$ .
Der Boden mit der Treppenstufe muss nicht saniert werden

Berechne, für wie viel Fläche die Farbe reichen muss, wenn nur die Säulen gestrichen werden sollen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
Berechnung der Mantelfläche einer Säule
Die zu streichende Fläche einer Säule berechnest du über die Formel zur Berechnung der Mantelfläche eines Zylinders:
$M_{S \ddot{a} u l e} = U \cdot h$
$U$ ist der Umfang der Säule und $h$ die Höhe.
In der Angabe siehst du, dass die Säule einen Durchmesser $d$ von $3 m$ hat. Du kannst damit den Umfang berechnen:
$U = 2 \cdot r \cdot π = d \cdot π$
Setze die Werte in die Formel oben ein.
$M_{Säule}$ $=$ $U \cdot h$
↓
Setze $U = d \cdot π$ ein.
$=$ $d \cdot π \cdot h$
↓
Setze $d = 3 m$ und $h = 20 m$ ein.
$=$ $3 m \cdot π \cdot 20 m$
$=$ $60 π m^{2}$
$\approx$ $188,50 m^{2}$
Jetzt hast du den Mantel einer Säule. Du brauchst aber 25 Säulen.
Berechnung der Mantelfläche aller Säulen
$M_{Säulen}$ $=$ $25 \cdot M_{Säule}$
↓
Rechne mit dem ungerundeten Wert und setze $M_{Säule} = 60 π m^{2}$ .
$=$ $25 \cdot 60 π m^{2}$
$=$ $1500 π m^{2}$
$=$ $4712,39 m^{2}$
Die Farbe muss für $4712,39 m^{2}$ reichen.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zuerst musst du überlegen, wie viele Säulen der Tempel hat. Die Angabe sagt dir, dass auf der Rückseite 9, auf der Vorderseite 10 und an jeder Breitseite jeweils 5 Säulen sind. Das Problem ist jetzt, dass die Ecksäulen nicht doppelt gezählt werden dürfen.
Du darfst also nur 3 Säulen auf jeder Breitseite zählen und die Vorder- und Rückseite. Insgesamt sind es also $3 + 3 + 9 + 10 = 25$ .
Dann musst du dir überlegen, welche Figur eine Säule ist, nämlich ein Zylinder. Du musst also die Zylinderoberfläche von den 25 Säulen ausrechnen. Allerdings brauchst du dazu nur die Mantelfläche, da der "Boden" und der "Deckel" nicht gestrichen werden können.

Das Dach bekommt einen wasserfesten Anstrich. Dazu wird alles gestrichen, was vom Regen erreicht werden kann, das heißt alles außer die Unterseite des Daches.

Berechne, für wie viel Fläche die wasserfeste Farbe reichen muss.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Oberflächenformeln von Körpern

Oberfläche der Seitendächer

Die Seitendächer sind Quader, dessen Oberfläche du so berechnen kannst:

O_{Q u a d e r} = 2 \cdot l \cdot b + 2 \cdot l \cdot h + 2 \cdot b \cdot h

( $l$ : Länge des Quaders, $b$ : Breite des Quaders, $h$ : Höhe des Quaders)

Überlege dir jetzt, welche Seiten wirklich gestrichen werden müssen. Du brauchst nur eine $l \cdot b$ Seite und nur eine $l \cdot h$ Seite und zwei $b \cdot h$ Seiten.

$O_{S e i t e n d a c h}$	$=$	$l \cdot b + l \cdot h + 2 \cdot b \cdot h$
	↓	Setze die gegebenen Werte ein: $l = 90 m : 3 = 30 m, h = 50 m, h = 5 m$
	$=$	$30 m \cdot 50 m + 50 m \cdot 5 m + 2 \cdot 30 m \cdot 5 m$
	$=$	$2050 m^{2}$

Das ganze brauchst du zwei mal, da es zwei Seitendächer gibt.

O_{S e i t e n d \ddot{a} c h e r} = 2 \cdot 2050 m^{2} = 4100 m^{2}

Oberfläche Mittelteil

Zur Oberfläche vom Mittelteil gelangst du, indem du

die zwei Seiten vom Spitzdach
die Vorder und Rückseite, die sich aus Rechteck und Dreieck zusammensetzen
die zwei Seitenflächen vom Vordach

ausrechnest. $A$ bezeichnet hier immer die Fläche.

A_{S p i t z d a c h O b e r s e i t e} = 2 \cdot l \cdot b

Die Seitenflächen brauchst du zweimal. Die Länge ist $60 m$ . Aber wie lang ist die Breite?

Berechnung der Breite des Seitendachs

Betrachte dazu das Dreieck, das du auf der Vorderseite siehst. Aus diesem musst du jetzt die fehlende Länge ausrechnen. Dies machst du mit dem Satz des Pythagoras.

Wie kommst du jetzt auf die fehlende Strecke?

$h^{2} + c^{2} = b^{2}$ $\Rightarrow$ $b = \sqrt{h^{2} + c^{2}}$ .

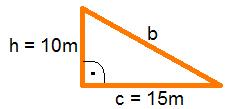
Setze die Werte ein.

$b$	$=$	$\sqrt{h^{2} + c^{2}}$
	↓	Setze $h = 10 m$ und $c = 30 m : 2 = 15 m$ ein.
	$=$	$\sqrt{{(10 m)}^{2} + {(15 m)}^{2}}$
	$=$	$\sqrt{100 m^{2} + 225 m^{2}}$
	$=$	$\sqrt{325 m^{2}}$
	↓	Zerlege $325$ in seine Primfaktoren um teilweise zu radizieren.
	$=$	$\sqrt{5 \cdot 5 \cdot 13} m$
	↓	Radiziere teilweise.
	$=$	$5 \sqrt{13} m$

Mit dieser Breite kannst du jetzt weiter rechnen.

Berechnung der Fläche der Oberseite des Spitzdachs

$A_{S p i t z d a c h O b e r s e i t e}$	$=$	$2 \cdot l \cdot b$
	↓	Die Breite hast du gerade ausgerechnet und die Länge ist $60 m$ .
	$=$	$2 \cdot 60 m \cdot 5 \sqrt{13} m$
	$\approx$	$2163,33 m^{2}$

Berechnung der Oberfläche des Spitzdachs vorne

A_{S p i t z d a c h V o r d e r s e i t e} = A_{D r e i e c k} + A_{R e c h t e c k}

Wie geht die Flächenformel für Dreiecke? Jetzt benötigst du aber wieder ein anderes Dreieck, nämlich das, was du auf der Vorderseite des Daches siehst.

$A_{S p i t z d a c h V o r d e r s e i t e}$	$=$	$A_{D r e i e c k} + A_{R e c h t e c k}$
	↓	Die Fläche des Dreiecks bestimmst du mithilfe der Höhe $h$ und die Länge der Grundseite $g$ .
	$=$	$\frac{1}{2} \cdot g \cdot h + l \cdot b$
	↓	Setze die gegebenen Werte ein: $g = 30 m, h = 10 m, l = 30 m$ und $b = 5 m$ .
	$=$	$\frac{1}{2} \cdot 30 m \cdot 10 m + 30 m \cdot 5 m$
	↓	Berechne.
	$=$	$300 m^{2}$

Da es sowohl eine Vorder- als auch eine Rückseite gibt, die den gleichen Flächeninhalt haben, kannst du die Fläche mal 2 nehmen.

A_{Spitzdach Vorderseite und Rückseite} = 2 \cdot 300 m^{2} = 600 m^{2}

Jetzt fehlen noch zwei kleine Seiten vom Vordach, mit der Länge $10 m$ und Breite $5 m$ .

$A_{S e i t e n f l \ddot{a} c h e n}$	$=$	$2 \cdot l \cdot b$
	↓	Setze die gegebenen Werte ein: $l = 10 m$ und $b = 5 m$
	$=$	$2 \cdot 10 m \cdot 5 m$
	$=$	$100 m^{2}$

Gesamtfläche Dach

\begin{array}{rcl} O_{g e s a m t} & = & O_{S e i t e n d \ddot{a} c h e r} \\ + A_{S p i t z d a c h O b e r s e i t e} \\ + A_{S p i t z d a c h V o r d e r s e i t e u n d R \ddot{u} c k s e i t e} \\ + A_{S e i t e n f l \ddot{a} c h e n} \end{array}

Setze die Werte ein. Am besten die genauen, ungerundeten Werte, ansonsten auf zwei Nachkommastellen gerundet.

\begin{array}{rcl} O_{g e s a m t} & = & 4100 m^{2} \\ + 2163,33 m^{2} \\ + 600 m^{2} \\ + 100 m^{2} \\ = & 6963,33 m^{2} \end{array}

Es wird also insgesamt so viel Farbe benötigt, dass sie für eine Fläche von $6963,33 m^{2}$ reicht.

Hast du eine Frage oder Feedback?

Kommentiere hier 👉

Wie viele $10 l$ Eimer Farbe werden für den ganzen Tempel benötigt, wenn ein Liter für $7 m^{2}$ reicht.

Oberfläche Tempel insgesamt
$O_{g e s a m t}$ $=$ $O_{D a c h} + O_{S \ddot{a} u l e n}$
↓
Setze die Werte aus Teilaufgabe a) und b) ein.
$\approx$ $6963,33 m^{2} + 4712,39 m^{2}$
$=$ $11675,72 m^{2}$
Wie viele Liter sind das?
Nenne die Anzahl der Liter $x$ . Schaue dir jetzt noch einmal die Angabe an. Es heißt: " $1 l$ reicht für $7 m^{2}$ ". Was sagt dir das?
Das bedeutet, dass man $7 m^{2}$ mit einem Liter Farbe streichen kann. Du musst nun also $O_{G e s a m t}$ durch 7 teilen, um die benötigte Menge an Farbe $x$ zu bestimmen.
$x$ $=$ $O_{g e s a m t} : 7 \frac{m^{2}}{l}$
↓
Setze $O_{G e s a m t}$ ein.
$=$ $11675,72 m^{2} : 7 \frac{m^{2}}{l}$
$=$ $1667,96 l$
Es werden also 1667,96 Liter benötigt.
Wie viele Eimer sind das?
Berechne nun die Anzahl $e$ der Eimer. In einem Eimer sind $10 l$ Farbe.
$e$ $=$ $\frac{x}{10 l}$
↓
Setze $x$ ein.
$=$ $\frac{1667,96 l}{10 l}$
$=$ $166,796$
Es werden also $166,796$ Eimer benötigt. Da man nur ganze Eimer kaufen kann, musst du immer aufrunden.
Antwort: Es werden 167 Eimer Farbe benötigt.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Zuerst musst du die Teilaufgaben a) und b) anschauen und zusammenrechnen, wie viel Quadratmeter Oberfläche du insgesamt ausgerechnet hast. Als nächstes musst du die Quadratmeter durch 7 teilen, um zu wissen, wie viele Liter du benötigst und anschließend nochmal durch 10 teilen, um die Anzahl der Eimer heraus zu finden.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$O$	$=$	$4 π r^{2}$	$: 4 π$
$\frac{O}{4 π}$	$=$	$r^{2}$	$\sqrt{}$

$M_{Säule}$	$=$	$U \cdot h$
	↓	Setze $U = d \cdot π$ ein.
	$=$	$d \cdot π \cdot h$
	↓	Setze $d = 3 m$ und $h = 20 m$ ein.
	$=$	$3 m \cdot π \cdot 20 m$
	$=$	$60 π m^{2}$
	$\approx$	$188,50 m^{2}$

$M_{Säulen}$	$=$	$25 \cdot M_{Säule}$
	↓	Rechne mit dem ungerundeten Wert und setze $M_{Säule} = 60 π m^{2}$ .
	$=$	$25 \cdot 60 π m^{2}$
	$=$	$1500 π m^{2}$
	$=$	$4712,39 m^{2}$

$O_{g e s a m t}$	$=$	$O_{D a c h} + O_{S \ddot{a} u l e n}$
	↓	Setze die Werte aus Teilaufgabe a) und b) ein.
	$\approx$	$6963,33 m^{2} + 4712,39 m^{2}$
	$=$	$11675,72 m^{2}$

$x$	$=$	$O_{g e s a m t} : 7 \frac{m^{2}}{l}$
	↓	Setze $O_{G e s a m t}$ ein.
	$=$	$11675,72 m^{2} : 7 \frac{m^{2}}{l}$
	$=$	$1667,96 l$

$e$	$=$	$\frac{x}{10 l}$
	↓	Setze $x$ ein.
	$=$	$\frac{1667,96 l}{10 l}$
	$=$	$166,796$

Gemischte Aufgaben zur Oberflächenberechnung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Mantelfläche

Kreisflächen

Gesamte Oberfläche

Hast du eine Frage oder Feedback?

Oberfläche des Würfels

Hast du eine Frage oder Feedback?

Oberfläche der Kugel

Hast du eine Frage oder Feedback?

Oberfläche der Pyramide

Grundfläche: Quadrat

Mantelfläche: Vier Dreiecke

Höhe der Seitenflächen

Seitenfläche

Mantelfläche

Oberfläche der Pyramide

Hast du eine Frage oder Feedback?

Berechnung der Mantelfläche einer Säule

Berechnung der Mantelfläche aller Säulen

Hast du eine Frage oder Feedback?

Oberfläche der Seitendächer

Oberfläche Mittelteil

Berechnung der Breite des Seitendachs

Berechnung der Fläche der Oberseite des Spitzdachs

Berechnung der Oberfläche des Spitzdachs vorne

Gesamtfläche Dach

Hast du eine Frage oder Feedback?

Oberfläche Tempel insgesamt

Wie viele Liter sind das?

Wie viele Eimer sind das?

Hast du eine Frage oder Feedback?