Gegeben sind eine Kugel mit dem Mittelpunkt und dem Radius sowie eine Ebene .
1) Zeige, dass die Ebene und die Kugel mehr als einen Punkt gemeinsam haben und berechne den Mittelpunkt und den Radius des Schnittkreises.
2) Berechne anschließend so, dass auf der Kugeloberfläche liegt.
3) Ermittle die Gleichung der Tangentialebene , welche die Kugel im Punkt berührt, in der Koordinatenform.
4) Bestimme die Gleichung einer zu parallelen Ebene in Koordinatenform, deren Schnittkreis mit der Kugel den Radius hat.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreis und Kugel
Teilaufgabe 1
Bestimmung der Art des Schnitts von Ebene und Kugel
Wandle die Parameterform der Ebene in eine Koordinatenform um.
Berechne den Normalenvektor der Ebene als Kreuzprodukt der beiden Richtungsvektoren.
Wähle einen beliebigen Punkt mit dem Ortsvektor , der in der Ebene liegt. Hier z.B. den Aufpunkt der Ebene:
Setze die Vektoren und in die allgemeine Normalenform ein und multipliziere das Skalarprodukt aus:
Das Skalarprodukt wird mit Hilfe des Distributivgesetzes ausmultipliziert:
Um die Hessesche Normalenform einer Ebene zu berechnen, teilt man die Ebenengleichung in Koordinatenform durch den Betrag des Normalenvektors . Der Normalenvektor wurde oben mit Hilfe des Kreuzproduktes berechnet. Wenn die Koordinatengleichung der Ebene gegeben ist, kann der Normalenvektor aus der Koordinatengleichung der Ebene abgelesen werden. Die Koeffizienten in der Ebenengleichung ergeben den Normalenvektor.
Setze nun die Koordinaten des Kugelmittelpunktes in die HNF ein:
Der Abstand des Kugelmittelpunktes von der Ebene beträgt und ist somit kleiner als der Kugelradius Die Ebene schneidet somit die Kugel in einem Schnittkreis.
Antwort: Damit ist gezeigt, dass die Ebene und die Kugel mehr als einen Punkt gemeinsam haben.
Berechnung des Mittelpunktes des Schnittkreises
Stelle die Gleichung der Lotgeraden von auf die Ebene auf, indem du für den Stützvektor den Vektor zum Kugelmittelpunkt und als Richtungsvektor den Normalenvektor der Ebene verwendest.
Schneide mit der Ebene :
Setze in die Geradengleichung ein und du erhältst den Vektor zum Mittelpunkt des Schnittkreises.
Antwort: Der Mittelpunktes des Schnittkreises hat folgende Koordinaten:
Bestimmung des Radius des Schnittkreises
Den Radius des Schnittkreises berechnest du mit Hilfe des Satzes von Pythagoras. (Anmerkung: In der Abbildung wird der Radius mit bezeichnet.)

Antwort: Der Radius des Schnittkreises beträgt etwa 2,98.
Zusätzliche Zeichnung zur Veranschaulichung
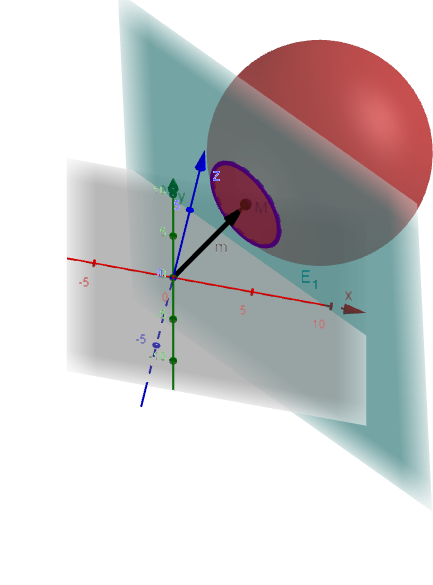
Teilaufgabe 2
Setze die Koordinaten von in die Kugelgleichung ein und berechne .
Die Kugel mit dem Mittelpunkt und dem Radius hat folgende Gleichung:
Setze die Koordinaten von und den Radius ein:
Wenn der Punkt auf der Kugeloberfläche liegen soll, müssen seine Koordinaten die Kugelgleichung erfüllen. Setze die Koordinaten ein und löse nach auf.
Da aber sein soll, gibt es nur die Lösung .
Antwort: Der Punkt mit den Koordinaten liegt auf der Kugeloberfläche.
Teilaufgabe 3
Die Gleichung für eine Tangentialebene im Punkt der Kugel mit dem Mittelpunkt lautet:
Setze und in ein:
Das Skalarprodukt wird mit Hilfe des Distributivgesetzes ausmultipliziert:
Antwort: Die obige Gleichung ist die Gleichung der Tangentialebene in Koordinatenform, die die Kugel im Punkt berührt.
Teilaufgabe 4
Eine zu T parallele Ebene hat den gleichen Normalenvektor wie die Ebene . Die rechte Seite der Ebenengleichung ist allerdings verschieden.
Eine zu parallele Ebene hat somit folgende Gleichung:
Die Unbekannte kannst du über die Bedingung, dass der Schnittkreisradius sein soll, bestimmen.
Wiederum gilt der Satz von Pythagoras: .
Mit und folgt:
Da der Abstand positiv sein soll gilt: .
Die Tangentialebene muss also den Abstand vom Kugelmittelpunkt haben.
Erstelle von die Hessesche Normalenform:
Setze nun die Koordinaten des Kugelmittelpunktes in die von ein und verlange, dass der Abstand sein soll.
Führe nun eine Fallunterscheidung durch:
Aus folgt:
Aus folgt:
Somit hast du zwei Lösungen gefunden.
Antwort: Es gibt zwei Ebenen die zu parallel sind und deren Schnittkreisradius mit der Kugel beträgt.
Zusätzliche Visualisierung
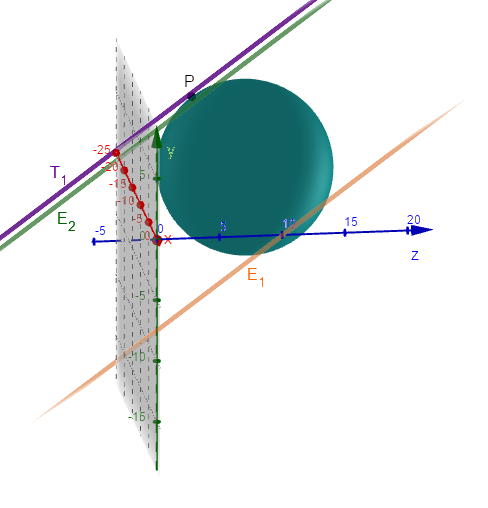
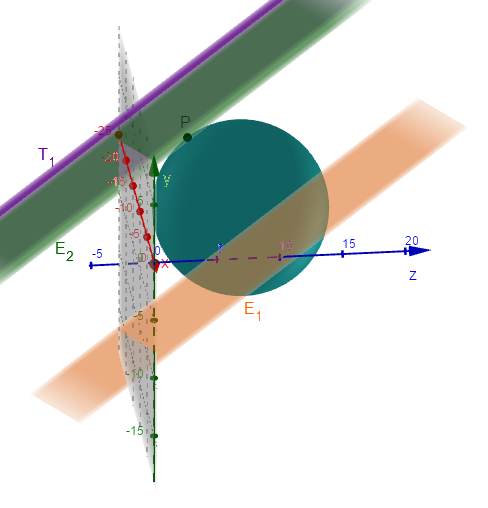
Du kannst die Aufgabe mit folgender Strategie lösen:
Strategie zu Teilaufgabe 1
Berechne den Abstand des Kugelmittelpunktes von der Ebene . Dazu benötigst du die Hessesche Normalenform. Wandle dazu die Parameterform der Ebene in eine Koordinatenform um. Aus der Koordinatenform erhältst du die Hessesche Normalenform. Setze den Kugelmittelpunkt in die Hessesche Normalenform ein und du erhältst den Abstand des Kugelmittelpunktes von der Ebene . Hier kannst du dann drei Fälle unterscheiden; die Ebene schneidet die Kugel, die Ebene berührt die Kugel oder es gibt keine gemeinsamen Punkte zwischen der Kugel und der Ebene.
Den Mittelpunkt des Schnittkreises berechnest du indem du die Lotgerade von auf die Ebene mit der Ebene schneidest.
Den Radius des Schnittkreises berechnest du mit Hilfe des Satzes von Pythagoras.
Strategie zu Teilaufgabe 2
Setze die Koordinaten von in die Kugelgleichung ein und berechne . Beachte, dass sein soll.
Strategie zu Teilaufgabe 3
Setze den berechneten Punkt in die Tangentialebenengleichung ein.
Strategie zu Teilaufgabe 4
Stelle die Gleichung einer zu parallelen Ebene mit unbekannter rechten Seite auf. Der Radius des Schnittkreises soll betragen. Das liefert die Bedingung für den Abstand des Kugelmittelpunktes zu . Aus dem berechneten Abstand und der der Ebene kannst du die unbekannte rechte Seite der parallelen Ebene berechnen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
