Analysis, Teil A, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion $f$ : $\;\displaystyle x\mapsto\frac{e^{2x}}{x}$ mit Definitionsbereich $D_f= \mathbb{R}\setminus$ {0}.
Bestimmen Sie Lage und Art des Extrempunktes des Graphen von $f$ .
(5 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema
Bilde die 1. Ableitung der Funktion $f$ .
Zur Berechnng der Ableitung kannst du die Quotientenregel benutzen.
Gegeben ist: $\;\;\;f(x)=\displaystyle \frac{e^{2x}}{x}\;\;\;\;\Rightarrow$
$\begin {array}{rcll}f'(x)&=&\displaystyle \underbrace{\frac {\overbrace{\color{red}{2} \cdot e^{2x}}^{\color{red}{\text{Kettenregel}}} \cdot x - 1\cdot e^{2x}}{x^{\color{red}{2}}}}_{\color{red}{\text{Quotientenregel}}}&|\;e^{2x}\;\text{ausklammern}\\&=&\displaystyle \frac{e^{2x}(2x-1)}{x^2}\end{array}$
Setze $f^{'} (x)$ gleich Null und löse die Gleichung:
$\def\arraystretch{1.25} \begin{array}{rcll}\displaystyle \frac{e^{2x}(2x-1)}{x^2}&=&0&\;|\,\cdot x^2\\\underbrace{e^{2x}}_{\color{red}{>0}}(2x-1)&=&\color{red}{0}&\;|:e^{2x}\\2x-1&=&0\\x&=&0{,}5\end{array}$
Setze $x = 0,5$ in $f (x)$ ein, um die 2. Koordinate des möglichen Extremums zu erhalten:
$f(0{,}5)=\displaystyle \frac{e^{2\cdot 0{,}5}}{0{,}5}=\frac{e}{0{,}5}=2e$
Der Punkt $M (0,5 ∣ 2 e)$ ist ein mögliches lokales Extremum.
Art des Extremums
Für das Vorliegen eines lokalen Extremums ist die Bedingung, dass die 1. Ableitung Null ist notwendig, aber nicht hinreichend.
Ob $M (0,5 ∣ 2 e)$ ein lokales Maximum, ein lokales Minimum oder aber ein Wendepunkt mit horizontaler Tangente ist, bestimmst du indem du entweder zeigst, dass
a) die 2. Ableitung für $x = 0,5$ ungleich Null ist oder
b) die 1. Ableitung bei $x = 0,5$ ihr Vorzeichen wechselt, d.h. die Funktionswerte links und rechts von $x = 0,5$ verschiedene Vorzeichen haben.
Berechnung der 2. Ableitung
$f'(x)=\displaystyle \frac{e^{2x}(2x-1)}{x^2}\quad\Rightarrow$
$\def\arraystretch{1.25} \begin{array}{rcll}f''(x)&=&\displaystyle\overbrace{\frac{\overbrace{[2e^{2x}(2x-1)+e^{2x}\cdot 2]}^{\color{red}{\text{Produktregel}}}\cdot x^2-2xe^{2x}(2x-1)}{x^{\color{red}4}}}^{\color{red}{\text{Quotientenregel}}}\\&=&\displaystyle\frac{x\cdot e^{2x}[(4x-2+2)\cdot x-4x+2]}{x^4}\\&=&\displaystyle\frac{x\cdot e^{2x}(4x^2-4x+2)}{x^4}\\&=&\displaystyle\frac{2e^{2x}(2x^2-2x+1)}{x^3}\end{array}$
Setze $x = 0,5$ in $f^{''} (x)$ ein:
$f''(0{,}5)=\displaystyle \frac{2\cdot e^1\cdot 0{,}5}{0{,}5^3}=8e\,\color{red}{>}0$
Daraus folgt, dass $M (0,5 ∣ 2 e)$ das lokale Minimum der Funktion $f$ ist.
Betrachtung des Vorzeichenwechsels der 1. Ableitung als alternativer Nachweis für die Extremwerteigenschaft des Punktes $M$ :
Der Nachweis, dass die Funktionswerte einer Funktion links bzw. rechts einer bestimmten Stelle $x_{0}$ verschiedenes Vorzeichen haben, ist bei Summentermen in der Regel nicht ohne weiteres möglich.
Ist der Funktionsterm aber ein Produkt, so liest du einen eventuellen Vorzeichenwechsel mühelos aus den Vorzeichen der einzelnen Faktoren ab.
Der Funktionsterm der Funktion $f^{'}$ ist das Produkt von drei Faktoren:
$f'(x)= \underbrace{e^{2x}}_{\text{1. Faktor}}\cdot \underbrace{(2x-1)}_\text{2. Faktor}\cdot \underbrace{x^{-2}}_{\text{3. Faktor}}$
Daraus liest du den Vorzeichenwechsel von $f^{'}$ ab:
Der 1. und der 3. Faktor sind "vorzeichenstabil". Sie sind sowohl für kleinere x-Werte als 0,5 wie auch für größere stets positiv.
Der 2. Faktor aber ist für $x < 0,5$ negativ und für $x > 0,5$ positiv.
Damit wechseln die Funktionswerte von $f^{'}$ - als Produktwerte - beim Durchgang von links nach rechts bei $x = 0,5$ ihr Vorzeichen von minus nach plus.
Für $x = 0,5$ ergibt sich also ein lokales Minimum.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die in $\mathbb{R}\setminus$ {0} definierte Funktion $f:x\mapsto1-\displaystyle\frac{1}{x^2}$ ,
welche die Nullstellen $x_{1} = - 1$ und $x_{2} = 1$ hat.
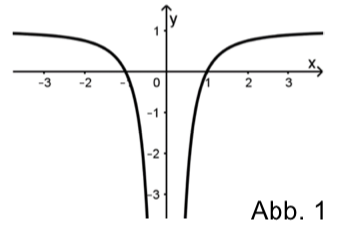
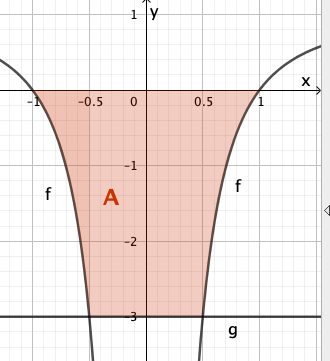
Abbildung1 zeigt den Graphen von $f$ , der symmetrisch bezüglich der y-Achse ist.
Weiterhin ist die Gerade $g$ mit der Gleichung $y = - 3$ gegeben.
a)
Zeigen Sie, dass einer der Punkte, in denen $g$ den Graphen von $f$ schneidet, die x-Koordinate $\frac12$ hat.
b)
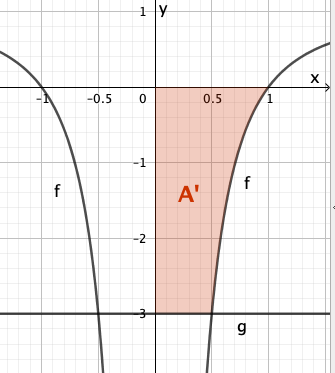
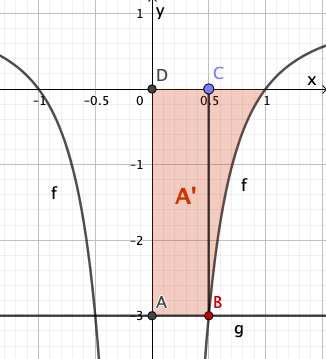
Bestimmen Sie rechnerisch den Inhalt der Fläche, die der Graph von $f$ , die x-Achse und die Gerade $g$ einschließen.

Im Zusammenhang mit einer gegebenen gebrochenrationalen Funktion ist ein Flächenstück zu berechnen.
Lösung Teilaufgabe a)
In dieser Teilaufgabe sind die beiden Funktionen
$f:x\mapsto 1-\frac{1}{x^2}$ und
$g:x\mapsto -3$
zu schneiden.
Setze die beiden Funktionsterme gleich und löse die Gleichung.
$\def\arraystretch{1.25} \begin{array}{rcll}\displaystyle 1-\frac{1}{x^2}&=&-3&|\cdot\,x^2\\ x^2-1&=&-3x^2&|+3x^2+1\\4x^2&=&1&|:4\\x^2&=&\displaystyle \frac{1}{4}&| \sqrt{}\\x_1&=&\displaystyle +\frac 12\\x_2&=&\displaystyle -\frac 12\end{array}$
Einer der beiden Schnittpunkte der Graphen von $f$ und $g$ ist der Punkt $S (0,5 ∣ - 3)$ .
Lösung Teilaufgabe b)
Die Teilaufgabe verlangt eine Flächenberechnung.
Schraffiere zunächst die zu berechnende Fläche in einer Skizze.
Achtung:
Gemeint ist eine Fläche, deren Rand allein aus Teilen des Graphen von $f$ , aus Teilen der x-Achse und Teilen des Graphen von $g$ besteht.
Die richtige Fläche
Eine falsche Fläche
Die Fläche $A^{'}$ ist deshalb nicht die gemeinte Fläche, da ihr Rand einen Teil der y-Achse enthält.
Dennoch ist $A^{'}$ hilfreich zur Berechnung der Fläche $A$ , da - wegen der Symmetrie des Graphen von $f$ zur y-Achse - gilt: $A=2\cdot A'$
So berechnest du die Fläche $A^{'}$ :
$\def\arraystretch{2} \begin{array}{rcll}A'&=&\text{Rechteck}_{ABCD}\;+\displaystyle{\big|}\int_{0{,}5}^1f\left(x\right)\mathrm{dx}\;{\big|}\\&=&\quad 0{,}5\cdot 3\quad\quad+\,\big |\displaystyle \int_{0{,}5}^1 (1-\frac{1}{x^2})\mathrm{dx}\,\big |&\text{Beachte:}\int \frac{1}{x^2}\mathrm{dx}=\int x^{-2}\mathrm{dx}=-x^{-1}+c\\&=&\quad\;\,1{,}5\quad\quad\quad+\big |\,\big [x+x^{-1}\big ]_{0{,}5}^1\,\big |\\&=&\quad\;\,1{,}5\quad\quad\quad +\big |(1+1)-(0{,}5+2) \big |\\&=&\quad\;\,1{,}5\quad\quad\quad+\quad\quad 0{,}5\\A'&=&\quad\;\;\,2\end{array}$
Damit gilt für die gesuchte Fläche $A$ der Teilaufgabe:
$\displaystyle A= 2 \cdot A'= 4$
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
a)
(3 BE)
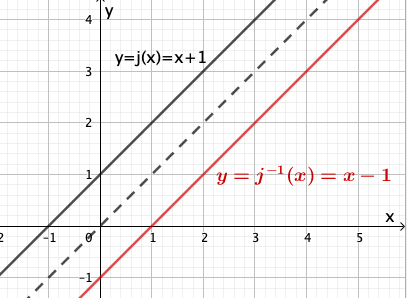
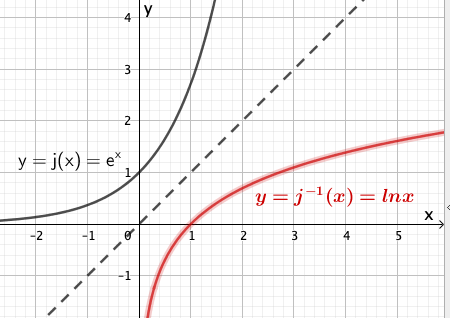
Betrachtet wird eine Schar von Funktionen $h_{k}$ mit $k\in\mathbb{R}^+$ , die sich nur in ihren jeweiligen Definitionsbereichen $D_{k}$ unterscheiden.
Es gilt $\;h_k:\,x\mapsto cos \,x$ mit $D_{k} = [0; k]$ .
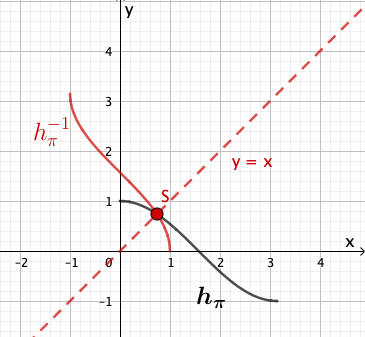
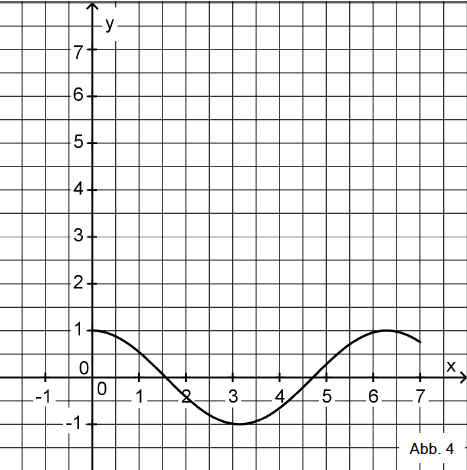
Abbildung 4 zeigt den Graphen der Funktion $h_{7}$ . Geben Sie den größtmöglichen Wert von $k$ an, sodass die zugehörige Funktion $h_{k}$ umkehrbar ist. Zeichnen Sie für diesen Wert von $k$ den Graphen der Umkehrfunktion von $h_{k}$ in Abbildung 4 ein und berücksichtigen Sie dabei insbesondere den Schnittpunkt der Graphen von Funktion und Umkehrfunktion.
b)
(2 BE)
Geben Sie den Term einer in $\mathbb{R}$ definierten und umkehrbaren Funktion $j$ an, die folgende Bedingung erfüllt: Der Graph von $j$ und der Graph der Umkehrfunktion von $j$ haben keinen gemeinsamen Punkt.
Im Teil a) sind die Funktionen einer Funktionenschar zu erkennen und zu unterscheiden. Zu einer umkehrbaren Funktion der Schar ist graphisch die Umkehrfunktion zu zeichnen.
Im Teil b) ist eine umkehrbare Funktion mit vorgegebenen Eigenschaften anzugeben.
Die Aufgabe verlangt Verständnis für die Bedeutung des Scharparameters in einer Funktionenschar und Kenntnisse zur Umkehrbarkeit von Funktionen.
Lösung Teilaufgabe a)
Die Funktionenschar besteht wegen $k\in \mathrm{R}^+$ aus unendlich vielen Graphen mit dem Funktionsterm $cos\,x$ , die alle bei $x = 0$ beginnen und für jedes gewählte $k$ bei $x = k$ enden, da gilt $D_{k} = [0; k]$ .
Die Graphen sind also Kosinusgraphen unterschiedlicher Länge.
Der größtmögliche Wert für $k$ , damit $h_{k}$ umkehrbar ist, ist $k=\pi$ .
Begründung:
Alle $h_{k}$ mit $0<k\leq\pi$ sind monton fallend und damit umkehrbar.
Lösung Teilaufgabe b)
Eine streng monotone in $\mathrm{R}$ definierte Funktion $j$ nimmt sicher keine Wert mehr als einmal an, daher ist es eine gute Idee, bei der Suche nach Beispielen damit zu beginnen.
Damit der Graph von $j$ und der Graph ihrer Umkehrfunktion $j^{- 1}$ keinen Punkt gemeinsam haben, darf der Graph von $j$ mit der Winkelhalbierenden $w:x\mapsto x$ keinen Punkt gemeinsam haben.
Beispiele sind:
Eine lineare Funktion: $j: x \mapsto x +c;\; c\neq 0$ mit $D=\mathrm{R}$
Die e-Funktion: $j:x\mapsto e^x$ mit $D=\mathrm{R}$ . Hierbei ist der Definitionsbereich der Umkehrfunktion allerdings nicht $\mathrm{R}$ , sonden nur das Intervall $(0,\infty)$ .
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
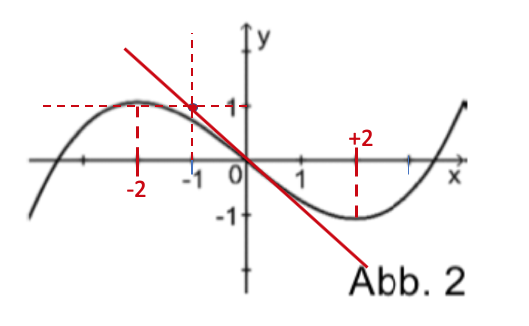
Die nebenstehende Abbildung 2 zeigt den Graphen einer Funktion $f$ .
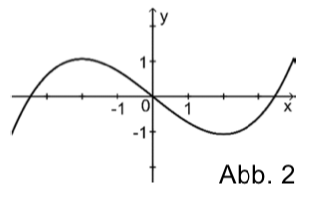
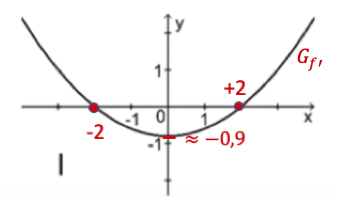
1. Einer der folgenden Graphen I, II und III gehört zur ersten Ableitungsfunktion von $f$ . Geben Sie diesen Graphen an. Begründen Sie, dass die beiden anderen Graphen dafür nicht infrage kommen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktionen
  Aus gegebenen Graphen sind charakteristische Eigenschaften der zugehörigen Funktionen zu erschließen bzw. im Rahmen der Zeichengenauigkeit vernünftig abzuschätzen.
  Infrage kommt nur der Graph I.
  Begründung:
  Der Graph der Funktion $f$ hat für die (geschätzten) Werte $x_{1} = - 2$ und $x_{2} = + 2$ lokale Extrema.
  Die Ableitungsfunktion $f^{'}$ der Funktion $f$ muss deshalb (etwa) für diese Werte Nullstellen haben.
  Damit scheidet Graph II aus.
  Dem Graphen von $f$ entnimmt man für $x = 0$ eine (Wende-)Tangente mit einer geschätzten Steigung von -1.
  Damit scheidet Graph III aus. Denn für diesen Graph gilt $f'(0)\approx-2$ . Der Graph I dagegen passt mit $\approx -0{,}9$ gut.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
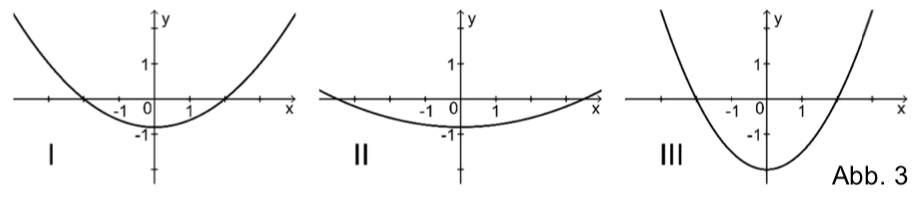
2. Die Funktion $F$ ist eine Stammfunktion von $f$ . Geben Sie das Monotonieverhalten von $F$ im Intervall $[1; 3]$ an. Begründen Sie Ihre Angabe.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktionen
  Die Lösung der Aufgabe verlangt die Vertrautheit mit dem Zusammenhang einer Funktion und einer ihrer Stammfunktionen und Kenntnis eines Monotoniekriteriums.
  Ergebnis:
  Jede Stammfunktion $F$ ist im Intervall $[1; 3]$ monoton fallend.
  Begründung:
  Für jede Stammfunktion $F$ ist $f$ die zugehörige Ableitungsfunktion.
  Da $f$ im Intervall $[1; 3]$ negativ ist, ist nach dem Monotoniekriterium differenzierbarer Funktion $F$ monoton fallend.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉