Stochastik, Teil A, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Ein Glücksrad besteht aus fünf gleich großen Sektoren. Einer der Sektoren ist mit "0" beschriftet, einer mit "1" und einer mit "2"; die beiden anderen Sektoren sind mit "9" beschriftet.
a)
(2 BE)
Das Glücksrad wird viermal gedreht. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Zahlen $2$ , $0$ , $1$ und $9$ in der angegebenen Reihenfolge erzielt werden.
b)
(3 BE)
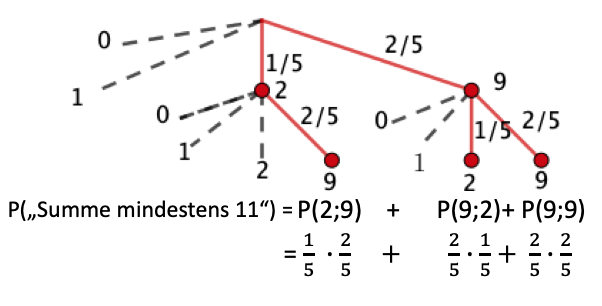
Das Glücksrad wird zweimal gedreht. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Summe der erzielten Zahlen mindestens $11$ beträgt.

In dieser Aufgabe musst du Wahrscheinlichkeiten von mehrstufigen Zufallsexperimenten am Beispiel eines Glücksrades berechnen.
Da die Sektoren gleich groß sind, kannst du davon ausgehen, dass beim einmaligen Drehen jeder Sektor mit der gleichen Wahrscheinlichkeit "gezogen" wird.
Wie die Zahlen den Sektoren zugeordnet sind, ist unerheblich.
Der Ergebnisraum des einmaligen Drehens des Glücksrads ist $Ω = {0; 1; 2; 9}$
Die obenstehende Graphik ist ein Beispiel, bei dem gerade das Ergebnis $0$ eingetreten ist.
Für die Wahrscheinlichkeiten der Elementarereignisse beim einmaligen Drehen erhältst du dann:
$P (0) = P (1) = P (2) = \frac{1}{5} und P (9) = \frac{2}{5} .$
Lösung der Teilaufgabe a)
Dass die Reihenfolge der Ergebnisse bei dem viermaligen Drehen mit $2 \to 0 \to 1 \to 9$ vorgegeben ist, macht die Berechnung der Wahrscheinlichkeit für dieses Ereignis leicht.
Es gilt: $P (2,0,1,9) = \frac{1}{5} \cdot \frac{1}{5} \cdot \frac{1}{5} \cdot \frac{2}{5}$
$P (2,0,1,9) = \frac{2}{625}$
Begründung:
Von einer Drehung zur anschließenden ist das Ergebnis vorgeschrieben und die 1. Pfadregel bei Baumdiagrammen erklärt das Ergebnis.
Du ersparst dir bei dieser Aufgabenstellung allerdings die aufwendige Zeichnung eines vierstufigen Baumdiagramms, da lediglich die Wahrscheinlichkeit eines einzigen Durchlaufs (Pfads) zu berechnen ist.
Die Wahrscheinlichkeit, dass beim viermaligen Drehen des Glücksrades die Zahlen in der angegebenen Reihenfolge erscheinen, beträgt 0,32 Prozent.
Lösung Teilaufgabe b)
Der Ergebnisraum beim zweimaligen Drehen des Glückrades besteht aus allen geordneten Zahlenpaaren der Zahlen $0,1,2,9$ .
Das Ereignis "Summe mindestens 11" erfasst die Paare $(2,9), (9,2), (9,9)$ .
Mit der Produktregel und der Summenregel für mehrstufige Experimente erhältst du:
$\begin{array}{rcll} P ("S. mind. 11") & = & P (2,9) + P (9,2) + P (9,9) \\ = & \frac{1}{5} \cdot \frac{2}{5} + \frac{2}{5} \cdot \frac{1}{5} + \frac{2}{5} \cdot \frac{2}{5} \\ = \frac{8}{25} \end{array}$
Das nachfolgende verkürzt gezeichnete zweistufige Baumdiagramm verdeutlicht die Berechnung.
Ergebnis:
Die Wahrscheinlichkeit, dass die Summe der erzielten Zahlen beim zweimaligen Drehen mindestens $11$ beträgt, ist 32 Prozent.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Zufallsgröße $X$ kann ausschließlich die Werte $1$ , $4$ , $9$ und $16$ annehmen. Bekannt sind $P (X = 9) = 0,2$ und $P (X = 16) = 0,1$ sowie der Erwartungswert $E (X) = 5$ . Bestimmen Sie mithilfe des Ansatzes für den Erwartungswert die Wahrscheinlichkeiten $P (X = 1)$ und $P (X = 4)$ .
(3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Erwartungswert
Die Zufallsgröße $X$ erfasst du mit folgender Tafel:
$x$
$1$
$4$
$9$
$16$
$P (X = x)$
$a$
$b$
$0,2$
$0,1$
Du hast also die beiden Unbekannten $a, b$ , mit $P (X = 1) = a$ und $P (X = 4) = b$ und benötigst zwei Bedingungen, um sie mithilfe eines linearen Gleichungssystems zu berechnen.
Eine Gleichung ergibt der gegebene Erwartungswert $E (X)$ von $X$ .
$E (X) = 1 \cdot a + 4 \cdot b + 9 \cdot 0,2 + 16 \cdot 0,1 = 5$
$\Rightarrow a + 4 b = 1,6$
Die zweite Gleichung liefert die Bedingung, dass die Summe aller einzelnen Wahrscheinlichkeiten der Verteilung von $X$ den Wert 1 ergibt.
$\Rightarrow a + b + 0,2 + 0,1 = 1$
$a + b = 0,7$
Damit hast du folgendes Gleichungssystem zu lösen:
$\begin{array}{rrcll} I & a + 4 b & = & 1,6 \\ II & a + b & = & 0,7 & | I - I I \\ I - II & 3 b & = & 0,9 & | : 3 \\ b & = & 0,3 & | b in I \\ a + 4 \cdot 0,3 & = & 1,6 & | - 1,2 \\ a & = & 0,4 \end{array}$
Ergebnis:
Die Wahrscheinlichkeit $P (X = 1)$ ist $0,4$ . Die Wahrscheinlichkeit $P (X = 4)$ ist $0,3$ .
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
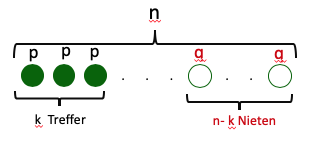
Gegeben ist eine Bernoullikette mit der Länge $n$ und der Trefferwahrscheinlichkeit $p$ . Erklären Sie, dass für alle $k \in {0; 1; 2; \dots; n}$ die Beziehung $B (n; p; k) = B (n; 1 - p; n - k)$ gilt.
(2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Bernoulliketten
$B (n; p; k)$ misst die Wahrscheinlichkeit von genau $k$ Treffern einer Bernoullikette der Länge $n$ mit der Trefferwahrscheinlichkeit $p$ .
Zu jeweils $k$ Treffern gehören $n - k$ Nieten mit der Nietenwahrscheinlichkeit $q = 1 - p$ .
Die Wahrscheinlichkeit für jedes $k \in {0; 1; 2; \dots; n}$ genau $n - k$ Nieten zu erhalten ist aber gleich $B (n; q; n - k)$ .
Somit gilt, wenn Treffer mit Nieten vertauscht werden:
$B (n; p; k) = B (n; 1 - p; n - k)$
Unnötig umständlich und zeitraubend kannst du die Behauptung auch wie folgt rechnerisch begründen:
Beginne mit der Berechnung der Wahrscheinlichkeit für genau $n - k$ "Treffern" bei der "Treffer"-wahrscheinlichkeit $1 - p$ .
$\begin{array}{rcll} B (n; 1 - p; n - k) & = & (\binom{n}{n - k}) \cdot (1 - p)^{n - k} \cdot [1 - (1 - p)]^{n - (n - k)} \\ = & (\binom{n}{n - k}) \cdot (1 - p)^{n - k} \cdot p^{k} \\ = & (\binom{n}{n - k}) \cdot p^{k} \cdot (1 - p)^{n - k} \\ = & (\binom{n}{k}) \cdot p^{k} \cdot (1 - p)^{n - k} \\ = & B (n; p; k) \end{array}$
Die Symmetrieeigenschaft der Binomialkoeffizienten zeigst du so:
$(\binom{n}{k}) = \frac{n!}{k! \cdot (n - k)!}$
$(\binom{n}{n - k}) = \frac{n!}{(n - k)! \cdot [n - (n - k)]!} = \frac{n!}{k! \cdot (n - k)!} = (\binom{n}{k})$

$x$	$1$	$4$	$9$	$16$
$P (X = x)$	$a$	$b$	$0,2$	$0,1$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Stochastik, Teil A, Aufgabengruppe 1

Lösung der Teilaufgabe a)

Lösung Teilaufgabe b)