Aufgaben zur skalaren Multiplikation und zu Vektorketten

1
Multipliziere den Vektor mit dem Skalar.
1. $5 \cdot (\begin{array}{c} 3 \\ 5 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalare Multiplikation
  $5 \cdot (\begin{array}{c} 3 \\ 5 \end{array})$
  Multipliziere komponentenweise.
  $= (\begin{array}{c} 5 \cdot 3 \\ 5 \cdot 5 \end{array}) = (\begin{array}{c} 15 \\ 25 \end{array})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $- 1 \cdot (\begin{array}{c} 3 \\ 1 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalare Multiplikation
  $- 1 \cdot (\begin{array}{c} 3 \\ 1 \end{array})$
  Multipliziere komponentenweise.
  $= (\begin{array}{c} - 1 \cdot 3 \\ - 1 \cdot 1 \end{array}) = (\begin{array}{c} - 3 \\ - 1 \end{array})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $\frac{7}{9} \cdot (\begin{array}{c} 27 \\ 22,5 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalare Multiplikation
  $\frac{7}{9} \cdot (\begin{array}{c} 27 \\ 22,5 \end{array})$
  Multipliziere komponentenweise.
  $= (\begin{array}{c} \frac{7}{9} \cdot 27 \\ \frac{7}{9} \cdot 22,5 \end{array}) = (\begin{array}{c} 21 \\ 17,5 \end{array})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Berechne den Lösungsvektor.
1. $(\begin{array}{c} 1 \\ 1 \end{array}) + 2 \cdot (\begin{array}{c} 1 \\ - 2 \end{array}) + (\begin{array}{c} 0 \\ 6 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren, Skalare Multiplikation
  $(\begin{array}{c} 1 \\ 1 \end{array}) + 2 \cdot (\begin{array}{c} 1 \\ - 2 \end{array}) + (\begin{array}{c} 0 \\ 6 \end{array})$
  Multipliziere zuerst den Vektor komponentenweise mit dem Skalar.
  $= (\begin{array}{c} 1 \\ 1 \end{array}) + (\begin{array}{c} 2 \cdot 1 \\ 2 \cdot (- 2) \end{array}) + (\begin{array}{c} 0 \\ 6 \end{array})$
  Addiere die Vektoren komponentenweise.
  $= (\begin{array}{c} 1 + 2 \cdot 1 + 0 \\ 1 + 2 \cdot (- 2) + 6 \end{array}) = (\begin{array}{c} 3 \\ 3 \end{array})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $4 \cdot (\begin{array}{c} 0 \\ - 2 \end{array}) + (\begin{array}{c} 6 \\ 0 \end{array}) - (\begin{array}{c} 0 \\ 3 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren und subtrahieren, Skalare Multiplikation
  $\begin{array}{l} 4 \cdot (\begin{array}{c} 0 \\ - 2 \end{array}) + (\begin{array}{c} 6 \\ 0 \end{array}) - (\begin{array}{c} 0 \\ 3 \end{array}) \end{array}$
  Multipliziere zuerst den ersten Vektor mit dem Skalar.
  $\begin{array}{l} = (\begin{array}{c} 0 \\ - 8 \end{array}) + (\begin{array}{c} 6 \\ 0 \end{array}) - (\begin{array}{c} 0 \\ 3 \end{array}) \end{array}$
  Addiere und subtrahiere die Vektoren komponentenweise.
  $= (\begin{array}{c} 0 + 6 - 0 \\ - 8 + 0 - 3 \end{array}) = (\begin{array}{c} 6 \\ - 11 \end{array})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $5 \cdot (\begin{array}{c} - 3 \\ 3 \end{array}) - 3 \cdot (\begin{array}{c} - 9 \\ 2 \end{array}) + 4 \cdot (\begin{array}{c} - 3 \\ - 2,25 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren und subtrahieren, Skalare Multiplikation
  $5 \cdot (\begin{array}{c} - 3 \\ 3 \end{array}) - 3 \cdot (\begin{array}{c} - 9 \\ 2 \end{array}) + 4 \cdot (\begin{array}{c} - 3 \\ - 2,25 \end{array})$
  Multipliziere die Vektoren komponentenweise mit den Skalaren.
  $= (\begin{array}{c} 5 \cdot (- 3) \\ 5 \cdot 3 \end{array}) - (\begin{array}{c} 3 \cdot (- 9) \\ 3 \cdot 2 \end{array}) + (\begin{array}{c} 4 \cdot (- 3) \\ 4 \cdot (- 2,25) \end{array})$
  Addiere bzw. subtrahiere komponentenweise.
  $= (\begin{array}{c} 5 \cdot (- 3) - 3 \cdot (- 9) + 4 \cdot (- 3) \\ 5 \cdot 3 - 3 \cdot 2 + 4 \cdot (- 2,25) \end{array}) = (\begin{array}{c} 0 \\ 0 \end{array})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Gegeben seien die Punkte $A (- 4 | 0)$ , $B (2 | - 1)$ und $C (5 | 2)$ . Vervollständige zu einem Parallelogramm ABCD und berechne neben den Koordinaten von D auch die Lage des Schnittpunktes M seiner Diagonalen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektorkette
Zeichnerische Bestimmung von D
Trage A, B und C ein. Übertrage den Vektor $\vec{B C}$ an A.
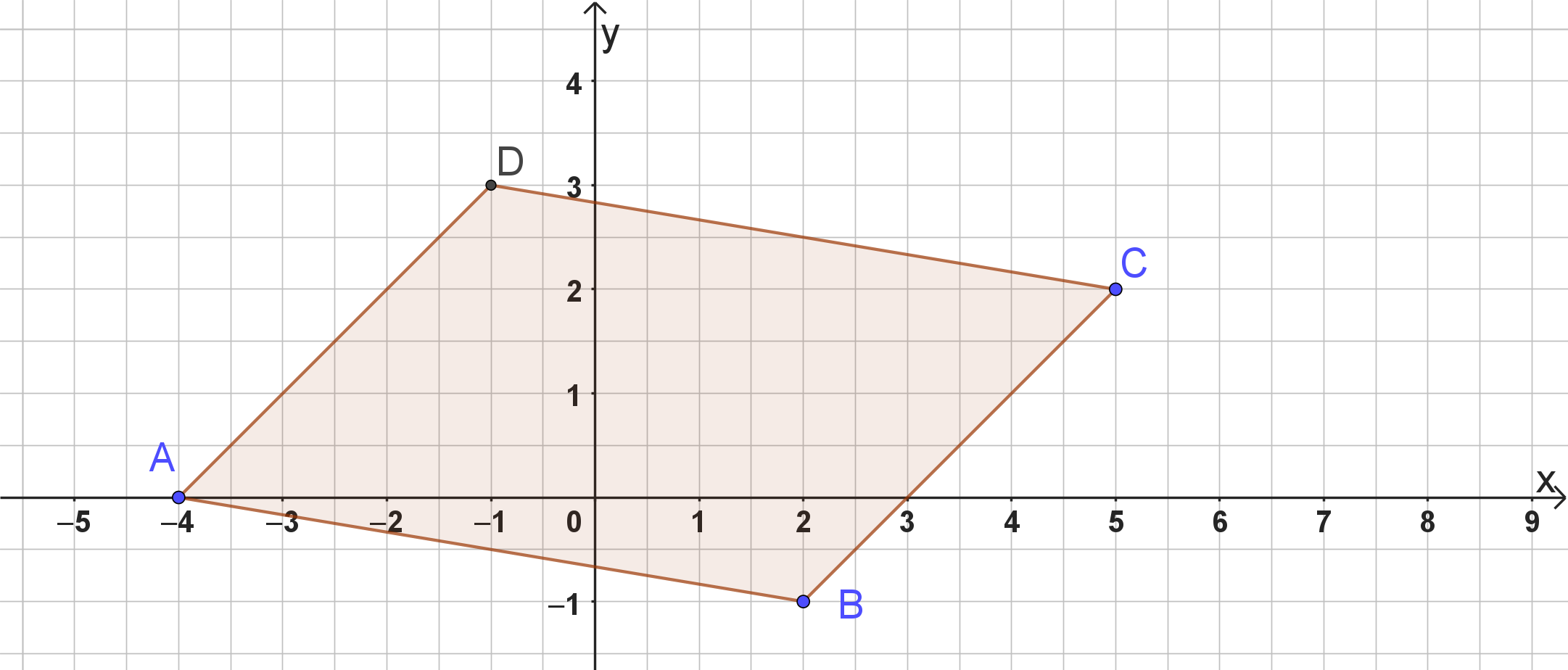
D liegt also bei $D (- 1 | 3)$
Da es sich nicht immer um so schöne Zahlwerte handelt, ist es gut, auch die rechnerische Bestimmung zu können.
Rechnerische Bestimmung
Bestimme zuerst $\vec{a} = \vec{A B}$ oder $\vec{b} = \vec{B C}$ .
$\vec{a} = (\begin{array}{cc} 2 - & (- 4) \\ - 1 & - 0 \end{array}) = (\begin{array}{c} 6 \\ - 1 \end{array})$
$\vec{b} = (\begin{array}{cc} 5 & - 2 \\ 2 - & (- 1) \end{array}) = (\begin{array}{c} 3 \\ 3 \end{array})$
Da $A B C D$ ein Parallelogramm ist, gilt außerdem $\vec{A B} = \vec{D C}$ und $\vec{B C} = \vec{A D}$ .
Die Koordinaten von D berechnest du, indem du eine Vektorkette bildest. Beginne diese mit dem Ortsvektor $\vec{A}$ von A.
$\vec{D} = \vec{A} + \vec{B C} = (\begin{array}{c} - 4 \\ 0 \end{array}) + (\begin{array}{c} 3 \\ 3 \end{array}) = (\begin{array}{c} - 1 \\ 3 \end{array})$
Somit ist $D (- 1 | 3)$ .
Lage des Diagonalenschnittpuntkts
In einem Parallelogramm halbieren sich die Diagonalen. Du suchst also den Mittelpunkt M der Strecke $A C$ oder $B D$ .
Bilde wieder eine Vektorkette:
$\vec{M} = \vec{A} + \frac{1}{2} \cdot \vec{A C} = (\begin{array}{c} - 4 \\ 0 \end{array}) + \frac{1}{2} \cdot (\begin{array}{c} 5 - (- 4) \\ 2 - 0 \end{array}) = (\begin{array}{c} - 4 \\ 0 \end{array}) + \frac{1}{2} \cdot (\begin{array}{c} 9 \\ 2 \end{array}) = (\begin{array}{c} 0,5 \\ 1 \end{array})$
Die Diagonalen schneiden sich also in $M (0,5 | 1)$
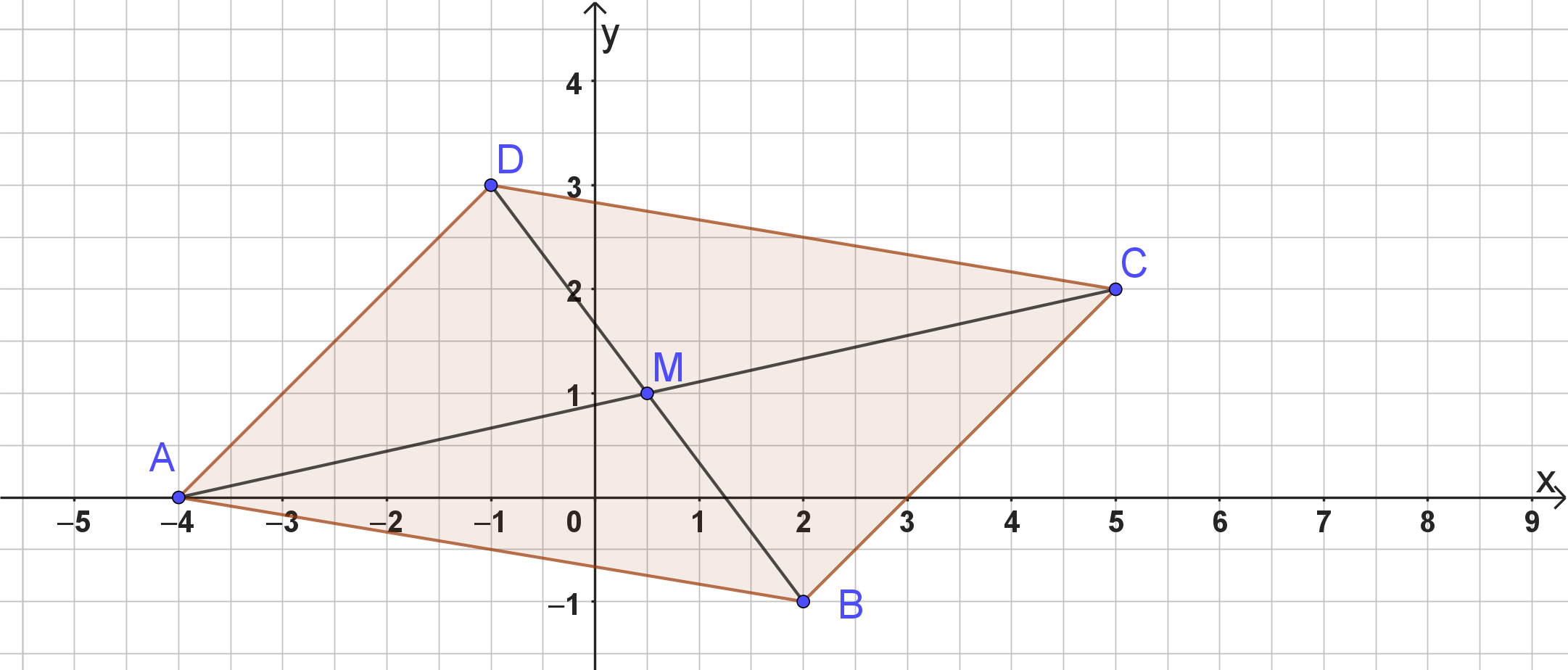
Löse durch Zeichnen oder mithilfe einer Vektorkette.
Nutze dabei, dass die Seiten $B C$ und $A D$ parallel und gleich lang sind.
Außerdem halbieren sich die Diagonalen im Parallelogramm.
4
Bestimme jeweils das Skalarprodukt der folgenden Vektoren:
1. $\begin{array}{l} v_{1} = (\begin{array}{c} - 2 \\ 7 \end{array}) \end{array}$ und $v_{2} = (\begin{array}{c} 5 \\ 3 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Das Skalarprodukt wird allgemein gebildet durch
  $\vec{a} \circ \vec{b} = (\begin{array}{c} a_{1} \\ a_{2} \end{array}) \circ (\begin{array}{c} b_{1} \\ b_{2} \end{array}) = a_{1} \cdot b_{1} + a_{2} \cdot b_{2} .$
  Hier also:
  ${\vec{v}}_{1} \circ {\vec{v}}_{2} = (\begin{array}{c} - 2 \\ 7 \end{array}) \circ (\begin{array}{c} 5 \\ 3 \end{array}) = (- 2) \cdot 5 + 7 \cdot 3 = - 10 + 21 = 11.$
  Das heißt: Das Skalarprodukt von ${\vec{v}}_{1}$ und ${\vec{v}}_{2}$ ist $11$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $\begin{array}{l} w_{1} = (\begin{array}{c} 1 \\ 3 \end{array}) \end{array}$ und $w_{2} = (\begin{array}{c} - 9 \\ 3 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Das Skalarprodukt wird allgemein gebildet durch
  $\vec{a} \circ \vec{b} = (\begin{array}{c} a_{1} \\ a_{2} \end{array}) \circ (\begin{array}{c} b_{1} \\ b_{2} \end{array}) = a_{1} \cdot b_{1} + a_{2} \cdot b_{2} .$
  Hier also:
  ${\vec{w}}_{1} \circ {\vec{w}}_{2} = (\begin{array}{c} 1 \\ 3 \end{array}) \circ (\begin{array}{c} - 9 \\ 3 \end{array}) = 1 \cdot (- 9) + 3 \cdot 3 = - 9 + 9 = 0$
  Hier stehen die Vektoren senkrecht aufeinander, da das Skalarprodukt $0$ ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $\begin{array}{l} c_{1} = (\begin{array}{c} - 8 \\ 1 \end{array}) \end{array}$ und $c_{2} = (\begin{array}{c} 0 \\ 6 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Das Skalarprodukt wird allgemein gebildet durch
  $\vec{a} ⊙ \vec{b} = (\begin{array}{c} a_{1} \\ a_{2} \end{array}) ⊙ (\begin{array}{c} b_{1} \\ b_{2} \end{array}) = a_{1} \cdot b_{1} + a_{2} \cdot b_{2} .$
  Hier also:
  ${\vec{c}}_{1} ⊙ {\vec{c}}_{2} = (\begin{array}{c} - 8 \\ 1 \end{array}) ⊙ (\begin{array}{c} 0 \\ 6 \end{array}) = (- 8) \cdot 0 + 1 \cdot 6 = 6$
  Das Skalarprodukt von ${\vec{c}}_{1}$ und ${\vec{c}}_{2}$ ist $6$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $\begin{array}{l} d_{1} = (\begin{array}{c} 0 \\ 107 \end{array}) \end{array}$ und $d_{2} = (\begin{array}{c} - 342 \\ 0 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Das Skalarprodukt wird allgemein gebildet durch
  $\vec{a} ⊙ \vec{b} = (\begin{array}{c} a_{1} \\ a_{2} \end{array}) ⊙ (\begin{array}{c} b_{1} \\ b_{2} \end{array}) = a_{1} \cdot b_{1} + a_{2} \cdot b_{2} .$
  Hier also:
  ${\vec{d}}_{1} ⊙ {\vec{d}}_{2} = (\begin{array}{c} 0 \\ 107 \end{array}) ⊙ (\begin{array}{c} - 342 \\ 0 \end{array}) = 0 \cdot (- 342) + 107 \cdot 0 = 0.$
  Das Skalarprodukt von ${\vec{d}}_{1}$ und ${\vec{d}}_{2}$ ist $0$ . Die Vektoren stehen somit senkrecht aufeinander.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $\vec{u} = (\begin{array}{c} 0,5 \\ - 1 \end{array})$ und $\vec{v} = (\begin{array}{c} 4 \\ 2 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Benutze die Formel zur Berechnung des Skalarprodukts:
  $\begin{array}{rcl} \vec{u} \circ \vec{v} & = & (\begin{array}{c} 0,5 \\ - 1 \end{array}) \circ (\begin{array}{c} 4 \\ 2 \end{array}) \\ = & 0,5 \cdot 4 + (- 1) \cdot 2 \\ = & 2 - 2 \\ = & 0 \end{array}$
  Das Skalarprodukt von $\vec{u}$ und $\vec{v}$ ist $0$ . (Die Vektoren stehen also senkrecht aufeinander.)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. $\vec{u} = (\begin{array}{c} 7 \\ 11 \end{array})$ und $\vec{v} = (\begin{array}{c} 0 \\ 1 / 2 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Benutze die Formel zur Berechnung des Skalarprodukts.
  $\begin{array}{rcl} \vec{u} \circ \vec{v} & = & (\begin{array}{c} 7 \\ 11 \end{array}) \circ (\begin{array}{c} 0 \\ 1 / 2 \end{array}) \\ = & 7 \cdot 0 + 11 \cdot 1 / 2 \\ = & 11 / 2 \\ = & 5,5 \end{array}$
  Das Skalarprodukt von $\vec{u}$ und $\vec{v}$ ist $5,5$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. $\vec{u} = (\begin{array}{c} 0 \\ - 3 π \end{array})$ und $\vec{v} = (\begin{array}{c} \sqrt{2} \\ 0 \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Tipp: Wenn du ganz genau hinschaust, musst du eigentlich nicht rechnen. An welcher Stelle kommt eine Null bei $\vec{u}$ vor? Und an welcher Stelle bei $\vec{v}$ ?
  Skalarprodukt berechnen
  Das Skalarprodukt zweier Vektoren kannst du anhand der Formel berechnen, wie du hier siehst. Oder du verwendest den Tipp und siehst die Antwort sofort.
  $\begin{array}{rcl} \vec{u} \circ \vec{v} & = & (\begin{array}{c} 0 \\ - 3 π \end{array}) \circ (\begin{array}{c} \sqrt{2} \\ 0 \end{array}) \\ = & 0 \cdot \sqrt{2} + (- 3 π) \cdot 0 \\ = & 0 - 0 \\ = & 0 \end{array}$
  Das Skalarprodukt von $\vec{u}$ und $\vec{v}$ ist $0$ . (Die beiden Vektoren stehen also senkrecht aufeinander.)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8. $\vec{a} = (\begin{array}{c} 2 \sqrt{2} \\ 45^{\circ} \end{array})$ und $\vec{b} = (\begin{array}{c} \sqrt{3} \\ 120^{\circ} \end{array})$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
  Tipp: Hier hast du es mit Polarkoordinaten zu tun.
  Skalarprodukt berechnen
  In dieser Aufgabe kannst du nicht sofort das Skalarprodukt berechnen, da du es mit Polarkoordinaten zu tuen hast, wie der Tipp bereits erwähnt. Deshalb musst du zuerst die Polarkoordinaten in kartesiche Koordinaten umrechnen und anschließend das Skalarprodukt berechnen.
  Umrechnung in kartesische Koordinaten
  Allgemein gilt für die Umrechnung eines Vektors in Polarkoordinaten $(r, φ)$ :
  $x = r \cdot \cos φ$ und $y = r \cdot \sin φ$
  Setze in diese Formel ein.
  $\vec{a}$ : $a_{1} = 2 \sqrt{2} \cdot \cos 45^{\circ} = 2 \sqrt{2} \cdot \frac{1}{\sqrt{2}} = 2$
  und $a_{2} = 2 \sqrt{2} \cdot \sin 45^{\circ} = 2 \sqrt{2} \cdot \frac{1}{\sqrt{2}} = 2$
  $\vec{b}$ : $b_{1} = \sqrt{3} \cdot \cos 120^{\circ} = \sqrt{3} \cdot (- \frac{1}{2}) = - \frac{\sqrt{3}}{2}$ und
  $b_{2} = \sqrt{3} \cdot \sin 120^{\circ} = \sqrt{3} \cdot \frac{\sqrt{3}}{2} = \frac{3}{2}$
  Damit erhältst du die folgenden Vektoren in kartesischer Form.
  $\vec{a} = (\begin{array}{c} 2 \\ 2 \end{array})$ und $\vec{b} = (\begin{array}{c} - \frac{\sqrt{3}}{2} \\ \frac{3}{2} \end{array})$
  Skalarprodukt berechnen:
  Das Skalarprodukt wird allgemein gebildet durch
  $\vec{a} \circ \vec{b} = (\begin{array}{c} a_{1} \\ a_{2} \end{array}) \circ (\begin{array}{c} b_{1} \\ b_{2} \end{array}) = a_{1} \cdot b_{1} + a_{2} \cdot b_{2}$ .
  Hier also:
  $\vec{a} \circ \vec{b} = (\begin{array}{c} 2 \\ 2 \end{array}) \circ (\begin{array}{c} - \frac{\sqrt{3}}{2} \\ \frac{3}{2} \end{array}) = 2 \cdot (- \frac{\sqrt{3}}{2}) + 2 \cdot \frac{3}{2} = - \sqrt{3} + 3 = 3 - \sqrt{3} \approx 1,27$
  Das Skalarprodukt von $\vec{a}$ und $\vec{b}$ ist somit $3 - \sqrt{3}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zur skalaren Multiplikation und zu Vektorketten

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Zeichnerische Bestimmung von D

Rechnerische Bestimmung

Lage des Diagonalenschnittpuntkts

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Skalarprodukt berechnen

Hast du eine Frage oder Feedback?

Skalarprodukt berechnen

Umrechnung in kartesische Koordinaten

Skalarprodukt berechnen:

Hast du eine Frage oder Feedback?