Gruppe A
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Bestimmen Sie für die Lösungen der Gleichung .
- 2
(Löse folgende Aufgaben.)
Eine der folgenden Mengen ist die maximale Definitionsmenge des Term . Kreuzen Sie (nur) diese an.
Begründen Sie anhand eines geeigneten Zahlenbeispiels, dass die in definierten Terme und nicht äquivalent sind.
- 3
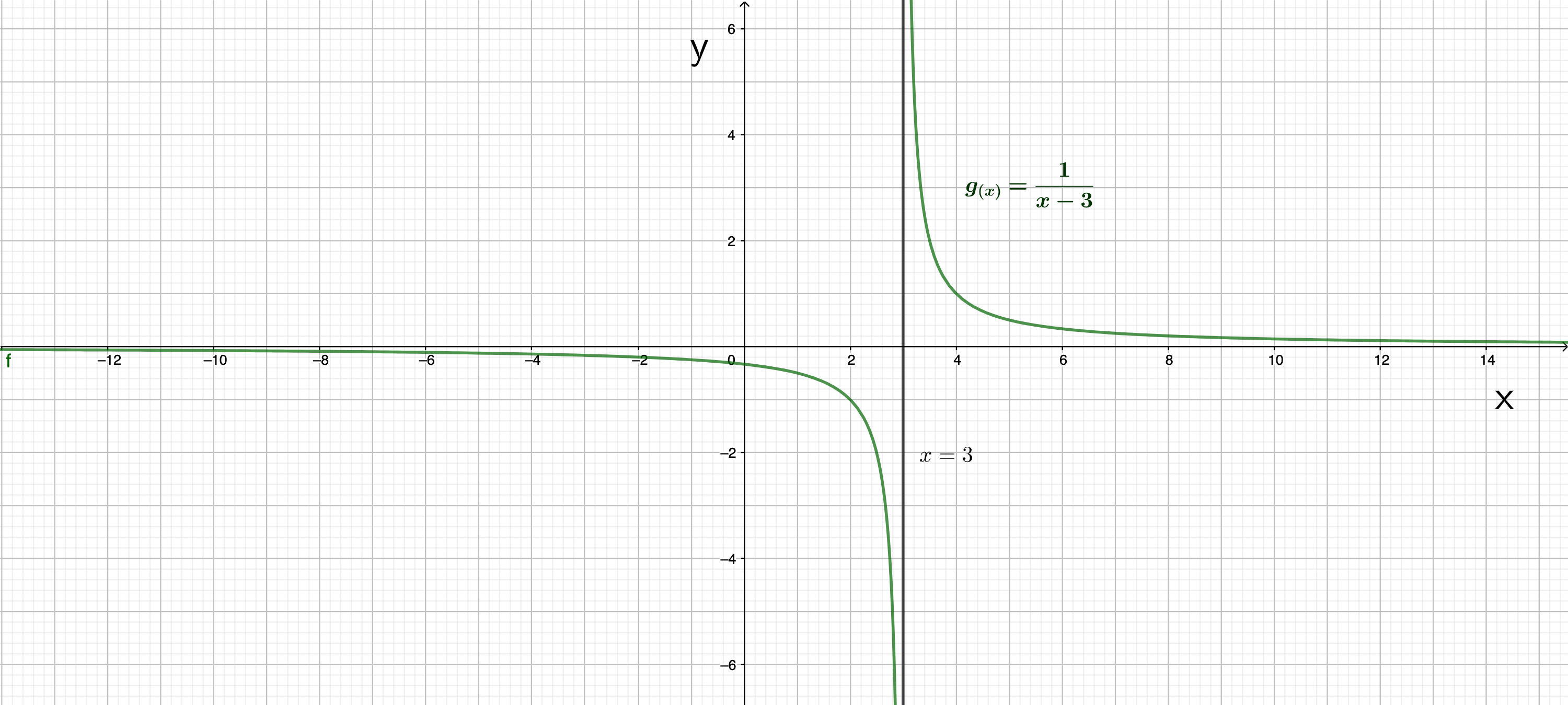
Geben Sie jeweils ein Beispiel für einen Funktionsterm an, der zum beschriebenen Graphen passt.
Der Graph der Funktion besitzt eine senkrechte Asymptote mit der Gleichung .
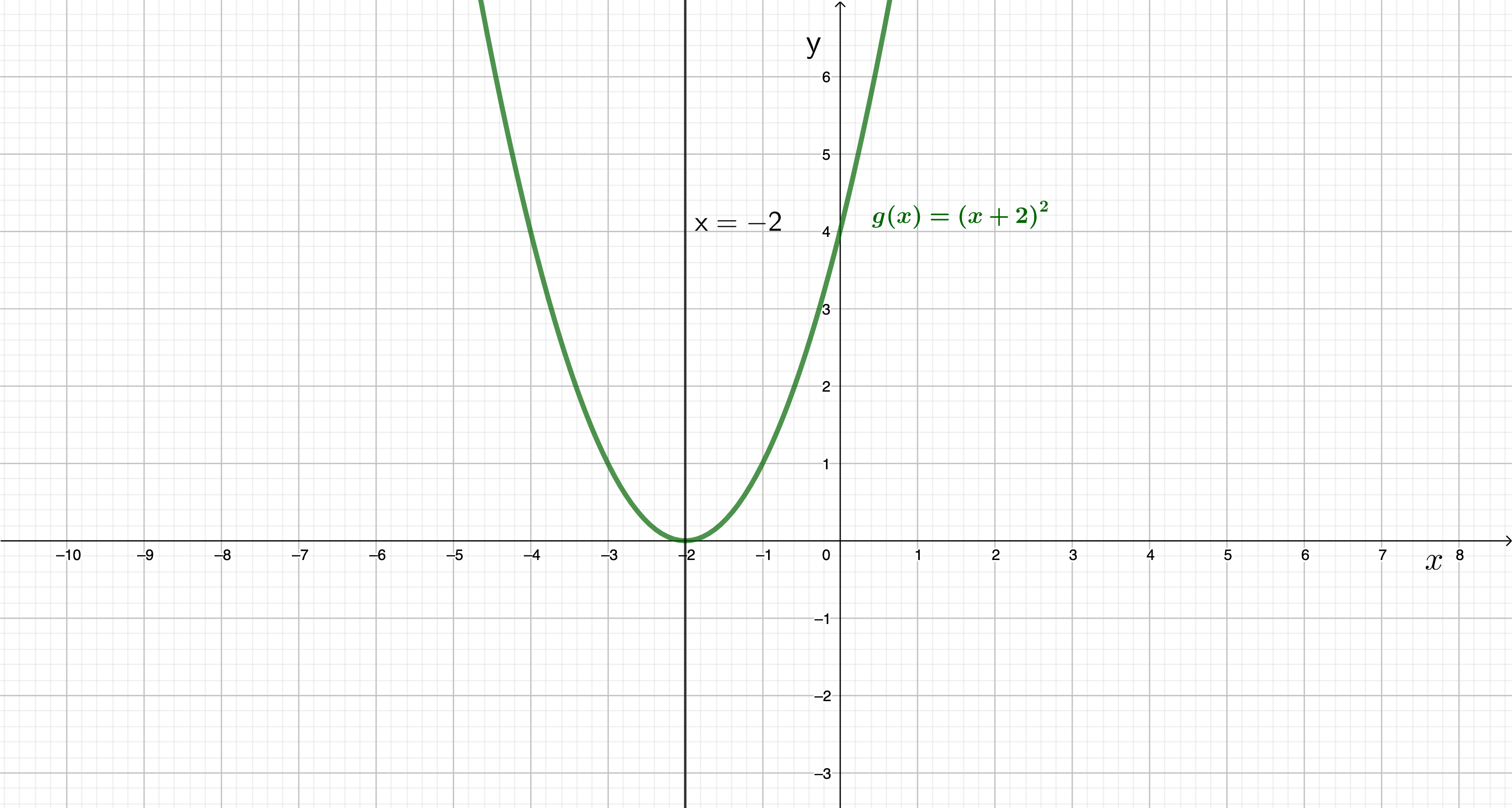
Der Graph der Funktion ist eine Parabel, die achsensymmetrisch zur Gerade mit der Gleichung ist.
- 4
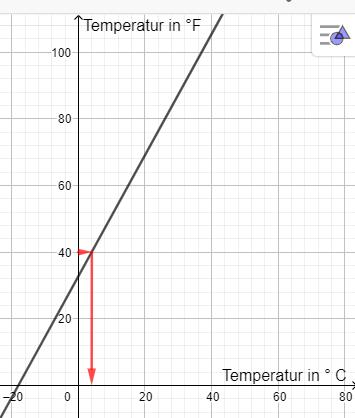
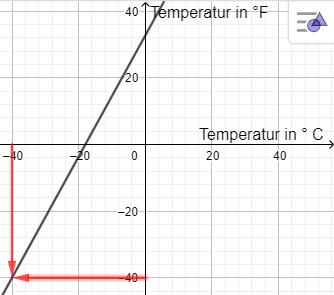
Temperaturen werden in den USA üblicherweise nicht in °C (Grad Celsius), sondern in °F (Grad Fahrenheit) angegeben. Der nebenstehende Graph ver-anschaulicht den Zusammenhang zwischen Temperaturangaben in °C und °F. Im abgebildeten Thermometer werden auf der linken Seite die Angaben in °F, auf der rechten in °C angetragen
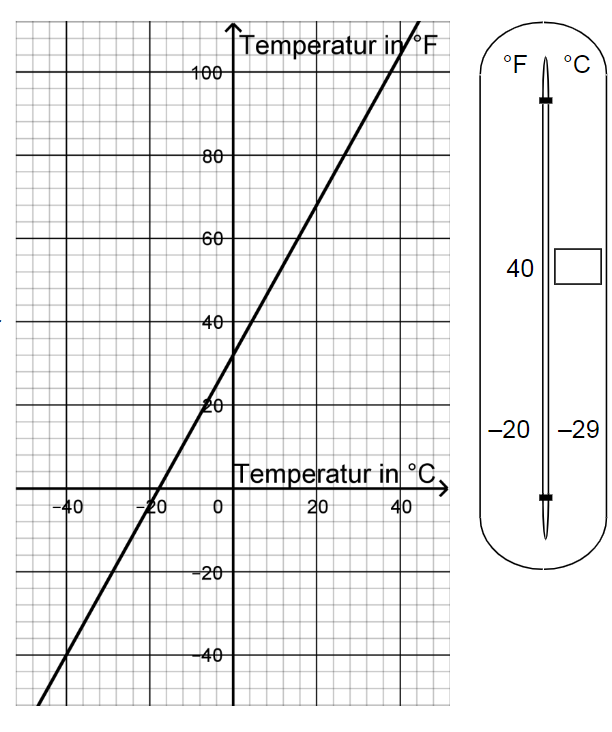
a) Lesen Sie aus dem Graphen ab, welche Angabe in °C einer Temperatur von 40°F in etwa entspricht, und tragen Sie den Wert im leeren Kästchen im Thermometer ein.
(Anmerkung: Auf serlo.org kannst du die Lösung in das Eingabefeld eingeben.)
°CEs gibt eine bestimmte Temperatur, bei der die Maßzahl der zugehörigen °C-Angabe die gleiche ist wie die der zugehörigen °F-Angabe. Lesen Sie diese Temperatur aus dem Graphen ab.
°C / °FMithilfe der Formel kann man eine Temperaturangabe in °F in eine Temperaturangabe in °C umrechnen. Lösen Sie die Formel nach auf. Geben Sie anschließend an, was sich damit als exakte Steigung der abgebildeten Gerade ergibt.
Bei der UN-Klimakonferenz in Paris wurde im Jahr 2015 beschlossen, die Erderwärmung im Vergleich zum vorindustriellen Zeitalter auf unter 2°C zu begrenzen. Ein amerikanischer Schüler hört von diesem „2-Grad-Ziel“ und interpretiert die Gradangabe als 2°F. Entscheiden Sie, ob ein Anstieg um 2°F größer oder kleiner ist als ein Anstieg um 2°C, und begründen Sie Ihre Entscheidung.
- 5
Das Diagramm stellt die Altersstruktur der Bevölkerung in Mittelfranken in den Jahren 1987 und 2016 dar. Dabei betrug die Gesamtbevölkerung in Mittelfranken im Jahr 1987 rund 1,5 Mio. und im Jahr 2016 rund 1,8 Mio. Personen.
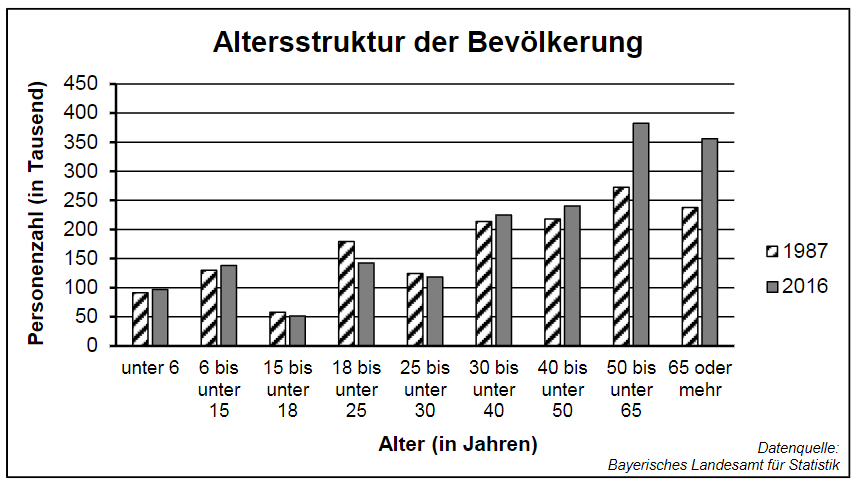
a) Die Personenzahl in der Altersgruppe der 50- bis unter 65-Jährigen hat von 1987 bis 2016 um einen bestimmten Prozentsatz zugenommen. Stellen Sie mithilfe geeigneter Zahlenwerte aus dem Diagramm einen Term auf, mit dem dieser Prozentsatz berechnet werden könnte.
b) Die Aussage „Etwa 20% der Bevölkerung sind 65 oder mehr Jahre alt.“ passt nur zu einem der beiden betrachteten Jahre. Geben Sie dieses Jahr an und begründen Sie Ihre Angabe.
c) Paul wundert sich, dass die beiden Säulen für die 15- bis unter 18-Jährigen so auffallend niedrig sind. Susi erklärt: „Das liegt nicht daran, dass diese Jahrgänge so besonders geburtenschwach sind, sondern es liegt an der Darstellung der Daten im Diagramm.“
Erläutern Sie, warum bei der gewählten Art der Darstellung tatsächlich zu erwarten ist, dass die Säule der 15- bis unter 18-Jährigen die kleinste ist, egal, ob man das Jahr 1987, das Jahr 2016 oder ein anderes Jahr betrachtet.
- 6
In einer Playlist eines Smartphones befinden sich 20 Lieder, darunter genau fünf mit deutschsprachigem Text. Die 20 Lieder werden in zufälliger Reihenfolge ohne Wiederholung abgespielt. ist die Wahrscheinlichkeit dafür, dass die ersten drei gespielten Lieder einen deutschsprachigen Text haben.
Erläutern Sie, warum der Ansatz falsch ist, und geben Sie einen richtigen Ansatz zur Berechnung von an.
- 7
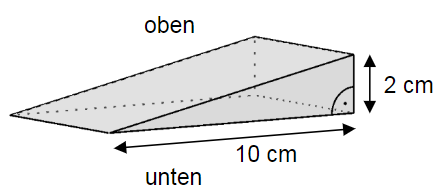
Ein rechtwinkliger Holzkeil ist 10 cm lang und 2 cm hoch (vgl. schematische Abbildung). Das dünne Ende wird so weit wie möglich unter eine Tür geschoben. Dann ist nur noch ein 8 cm langes Stück des Keils zu sehen. Berechnen Sie die Höhe des Spalts unter der Tür.
- 8
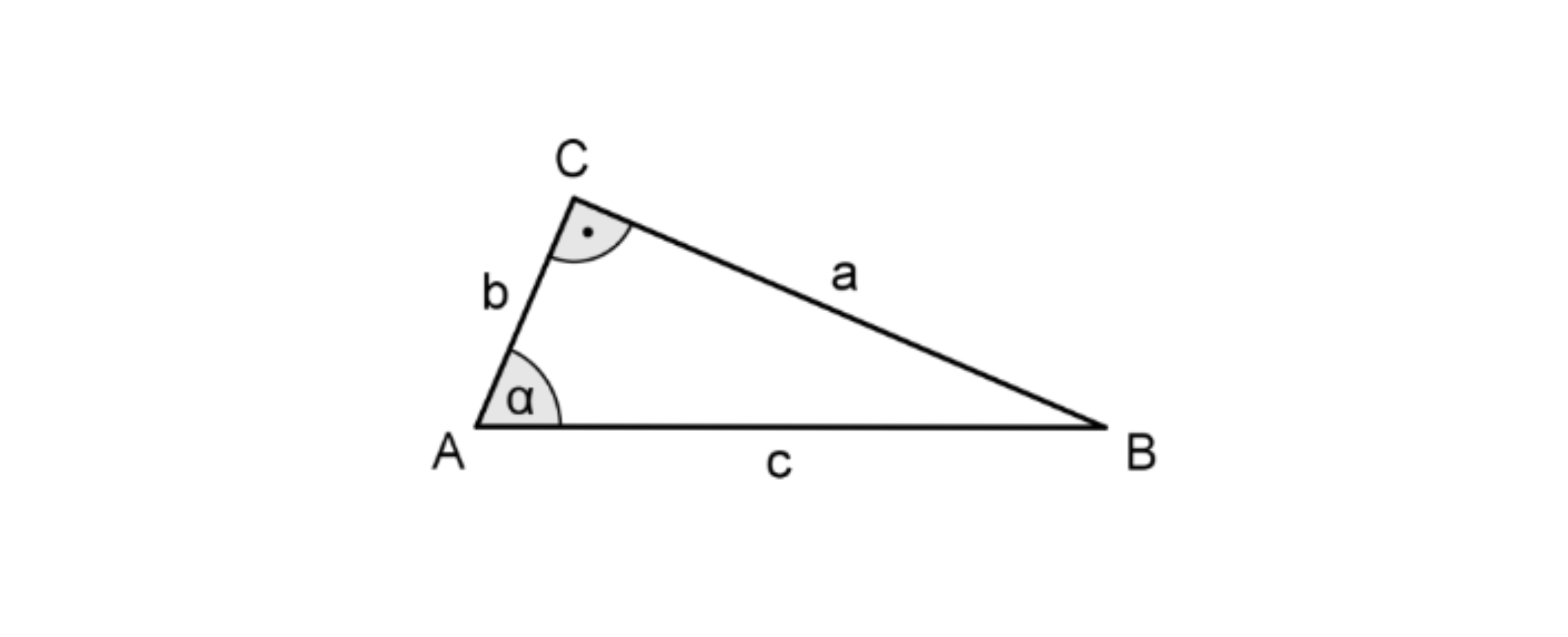
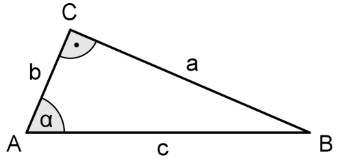
Betrachtet werden rechtwinklige Dreiecke mit rechtem Winkel bei und den in nebenstehender Abbildung verwendeten Bezeichnungen.
a) Berechnen Sie die Seitenlänge , falls gilt: und .
b) Drücken Sie allgemein, also unabhängig von den in Teilaufgabe a) betrachteten Zahlenwerten, und durch die Seitenlängen , und aus und zeigen Sie mithilfe dieser Ausdrücke, dass in jedem rechtwinkligen Dreieck gilt: .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?