Aufgaben zur Konstruktion besonderer Vierecke und zur Lösung geometrischer Problemstellungen
- 1
Winkelberechnungen am Trapez
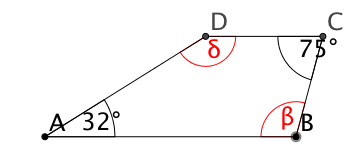
Im Trapez gelte , , . Berechne und !
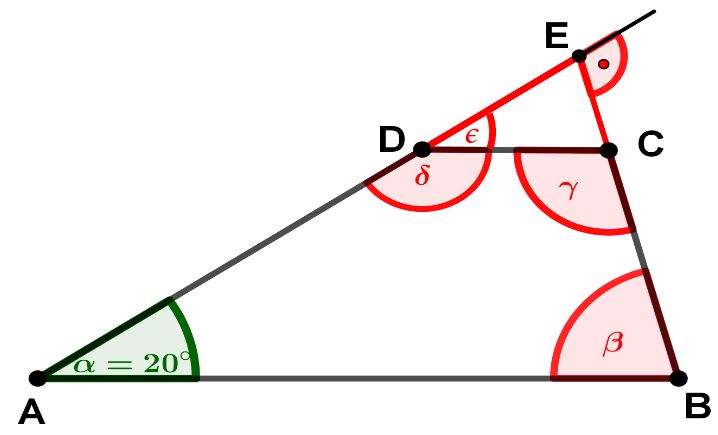
Im Trapez gelte , , . Berechne !
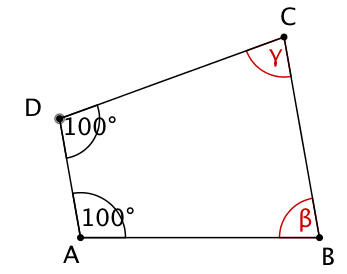
Im Trapez gelte: . Berechne und !
- 2
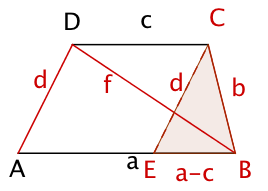
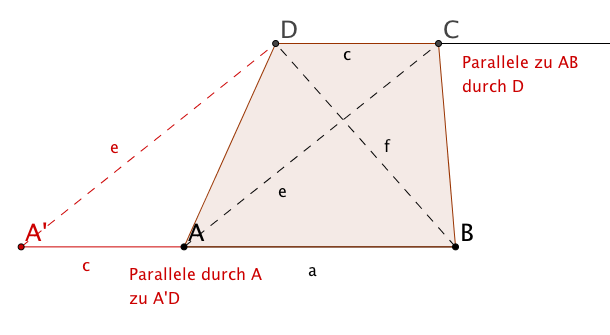
Konstruiere ein Trapez aus der gegebenen Länge der Differenz der beiden Grundseitenlängen , den Schenkellängen und sowie der Diagonalenlänge .
- 3
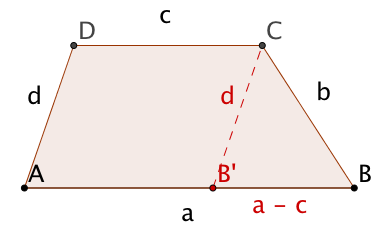
Konstruiere ein Trapez aus den Grundseitenlängen und sowie den Diagonalenlängen und .
- 4
Konstruiere ein Trapez aus den Seitenlängen
.
- 5
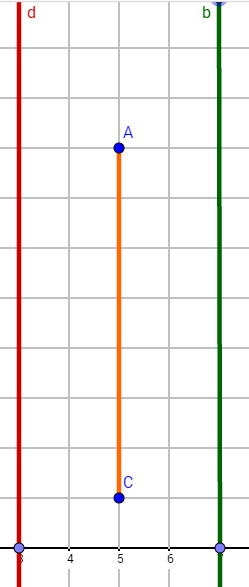
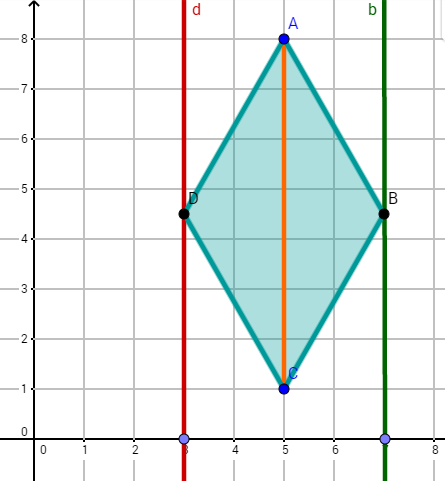
Zeichne zuerst die Punkte , und die Gerade in ein Koordinatensystem.
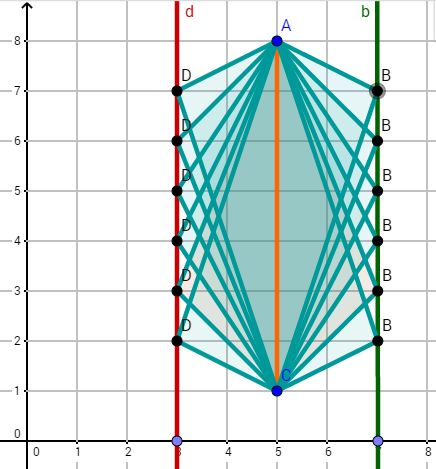
Die Punkte und liegen auf der Geraden . Ergänze die Dreiecke und jeweils zu einem Drachenviereck bzw. .
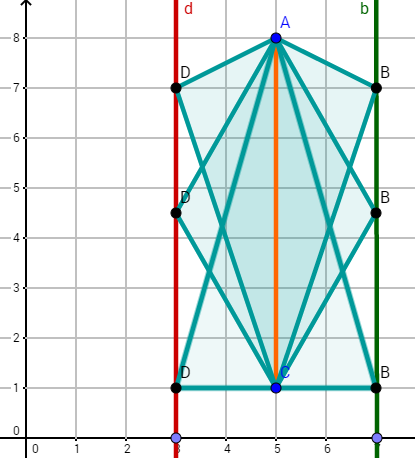
Für jeden Punkt auf der Geraden kann man das Dreieck zu einem Drachenviereck ergänzen. Alle Punkte liegen auf einer Geraden. Zeichne diese ein.
Nenne zwei Beispiele für die Punkte und , die auf den jeweiligen Geraden und liegen, dass das Drachenviereck entsteht.
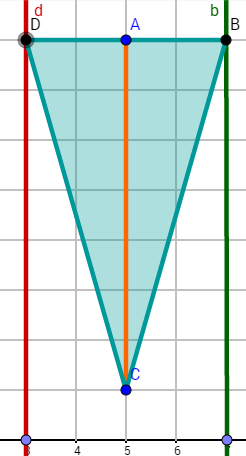
Wann ist das Drachenviereck eine Raute? Versuche und jetzt so zu verschieben, dass sie mit oder mit ein Dreieck bilden?
Was fällt dir im Bezug auf die verschiedenen Drachendreiecke/Raute/Dreiecke am Flächeninhalt auf?
- 6
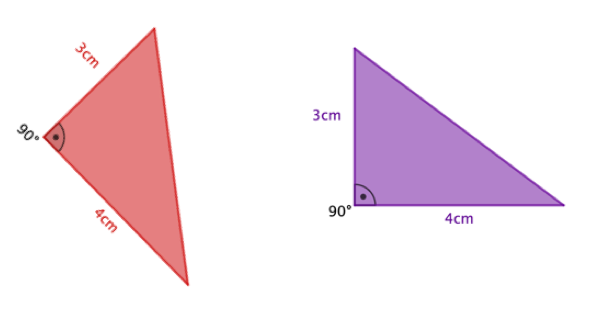
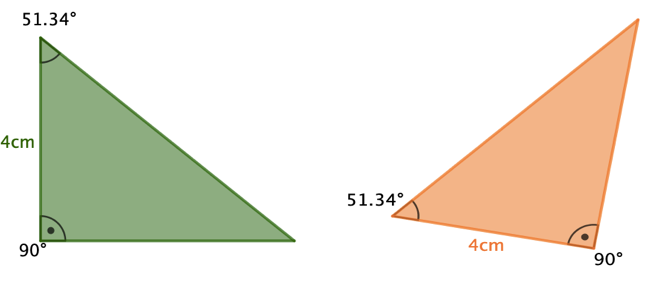
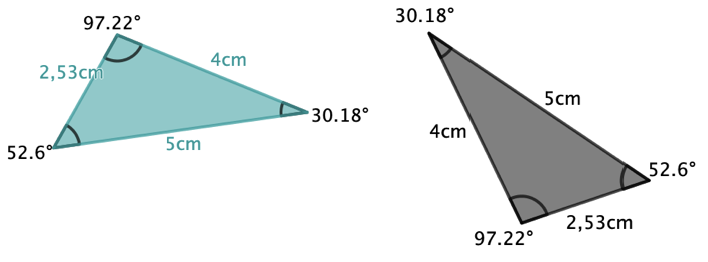
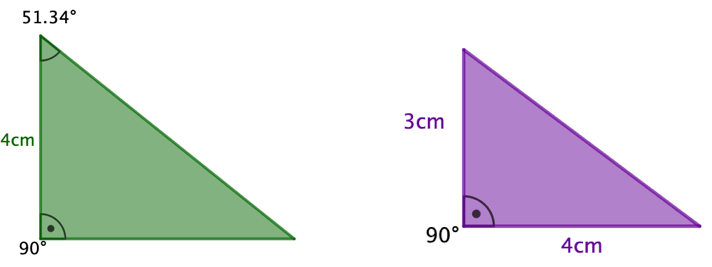
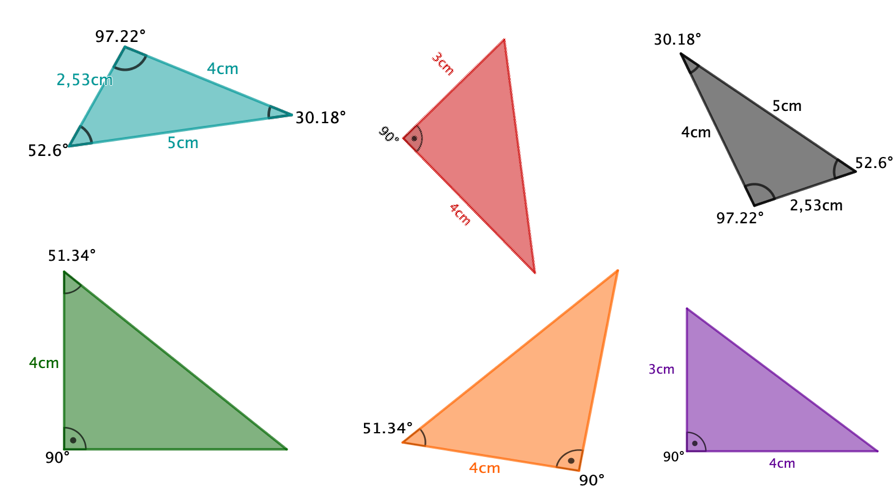
Welche der folgenden Dreiecke sind zueinander kongruent? Begründe deine Antwort mit einem passenden Kongruenzsatz.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?