Zum Einzeichnen des Dreiecks mit $\varphi=50°$ gehst du am besten so vor, dass du als Erstes $\frac{\varphi}{2}=25°$ an beiden Seiten von $[\mathrm{CM}]$ anträgst (rote Winkel in der Zeichnung). Dadurch erhältst du einen Winkel von $\varphi=50°$ und erfüllst die Aufgabenstellung.

Damit du die Höhe gleich bleibt sind die Eckpunkte des neuen Dreiecks die Schnittpunkte deiner "Winkelschenkel" (orangene Halbgeraden) mit der Strecke $[AB]$.

Das neue Dreieck $A_2 B_2 C$ ist in der Zeichnung orange hinterlegt.

Lösungsideen und Hinweise:

• In der Aufgabe steht, dass $\mathrm{A}(\varphi)=25\cdot \tan\frac{\varphi}{2}\ \mathrm{cm^2}$ ist. Das heißt allerdings nicht, dass man das verwenden darf, sondern nur, dass man es als Ergebnis herausbekommen soll, wenn man den Flächeninhalt der Dreiecke $\mathrm{A_n B_n C}$ bestimmt. $\rightarrow$ Rechne daher so, als sei der Flächeninhalt von Dreieck $\mathrm{A_n B_n C}$ gesucht und versuche, dabei auf die Formel zu kommen.

• "in Abhängigkeit von $\varphi$" heißt, dass $\varphi$ im Ergebnis stehen bleiben darf und kein Wert für $\varphi$ eingesetzt werden soll (insbesondere also weder die 80° aus der Angabe zur Aufgabenstellung noch die $50°$ aus A.1.1).

Formel für Flächeninhalt $\Delta A_n B_n C$ in Abhängigkeit von $\varphi$ aufstellen

Es gibt verschiedenen Arten, um den Flächeninhalt eines Dreiecks zu berechnen. Hier in diesem Fall

• versuchst du es am besten mit der Formel $A_{\Delta}=\frac{1}{2}\cdot g\cdot h$

• und nimmst dabei

• als Grundlinie $g$ die Strecke $[\mathrm {A_n B_n}]$

• und als Höhe $h$ die Strecke $[\mathrm{CM}]$.

$A_{\Delta }=\frac{1}{2}\cdot \overline{\mathrm{A_nB_n}}\cdot \overline{\mathrm{CM}}$

In der Aufgabe ist $\overline{\mathrm{CM}}=5\, \mathrm{cm}$ angegeben. Das ist unabhängig davon, wie groß $\varphi$ ist.

$A_{\Delta}=\frac{1}{2}\cdot \overline {\mathrm {A_n B_n}}\cdot 5 \, \mathrm{cm}$

$\frac{1}{2}\cdot \overline{\mathrm{A_nB_n}}$ kannst du zu $\overline {\mathrm {A_n M}}$ zusammenfassen oder du setzt $\overline{\mathrm{A_nB_n}}=2\cdot\overline{\mathrm{A_nM}}$ in die Formel ein und vereinfachst:

Term für $\overline {\mathrm {A_n M}}$ aufstellen

Zur Bestimmung von $\overline {\mathrm {A_n M}}$ betrachte das Dreieck $\Delta \mathrm{A_n M C}$ (oranges Dreieck).

$\Delta \mathrm{A_n M C}$ ist rechtwinklig. Daher kannst du die Formeln für Sinus, Kosinus und Tangens im rechtwinkligen Dreieck verwenden.

Stelle den Tangens auf, weil dieser in der angegebenen Formel verwendet wird.

$\tan (\frac{\varphi }{2})=\dfrac{\overline{\mathrm{A_nM}}}{\overline{\mathrm{CM}}}$

Die Formel für $\tan(\frac{\varphi}{2})$ stellst du nach $\overline {\mathrm {A_n M}}$ um, indem du mit ${\overline {\mathrm {C M}}}$ multiplizierst.

$\tan (\frac{\varphi }{2})=\dfrac{\overline{\mathrm{A_nM}}}{\overline{\mathrm{CM}}}\quad |\cdot \overline{\mathrm{CM}}$

$\tan (\frac{\varphi }{2})\cdot \overline{\mathrm{CM}}=\overline{\mathrm{A_nM}}$

Für $\overline {\mathrm {C M}}$ kannst du natürlich wieder $5 \, \mathrm{cm}$ einsetzen.

${\overline {\mathrm {A_n M}}} =\tan(\frac{\varphi}{2})\cdot5 \, \mathrm{cm}$

Dadurch erhältst du für ${\overline {\mathrm {A_n M}}}$ einen Term, den du in den Term von oben

$A_{\Delta}=\overline {\mathrm {A_n M}}\cdot 5 \, \mathrm{cm}$ einsetzen kannst.

Formel zusammensetzen

Damit hast du - wenn du die Faktoren vertauscht - das gewünschte Ergebnis erhalten und gezeigt, dass gilt:

$A(\varphi)=25\cdot \tan\frac{\varphi}{2}\ \mathrm{cm^2}$

Lösungsideen

Gegeben:

Der Flächeninhalt von $\mathrm{A_3 B_3 C}$ ist um $25\ \%$ größer als der Flächeninhalt von $\mathrm{A_2 B_2 C}$

Lösungsplan:

1. Berechne zuerst den Flächeninhalt von $\mathrm{A_2 B_2 C}$, indem du $\varphi = 50°$ in die Formel für $A(\varphi)$ einsetzt.

• Berechne $125\ \%$ von der Zahl, die du als Flächeninhalt erhalten hast. Das ist dann der Wert des Flächeninhalts von $\mathrm{A_3 B_3 C}$.

• Setze diesen Wert mit dem Term aus der Formel von $A(\varphi)$ gleich und löse dann nach $\varphi$ auf.

Lösung

Fläche des Dreiecks $\mathrm{A_2 B_2 C}$ berechnen

Für das Dreieck $\mathrm{A_2 B_2 C}$ ist nach Aufgabe (a) der Wert von $\varphi=50°$.

Setze $\varphi =50°$ in die Formel $A(\varphi)=25\cdot \tan\frac{\varphi}{2}\ \mathrm{cm^2}$aus A.1.2 ein.

$A(50°)=25\cdot \tan \frac{50°}{2}\ \mathrm{cm^2}$

Rechne das mit dem Taschenrechner aus.

Du darfst das Ergebnis auf 2 Stellen nach dem Komma runden.

$A_{\mathrm{A_2 B_2 C}}=A(50°)\approx 11{,}66\, \mathrm{cm^2}$

(Für die weitere Rechnung ist es aber besser, wenn du das Ergebnis ungerundet speicherst und damit weiterrechnest; auf zwei Stellen nach dem Komma gerundet wird dann erst das Endergebnis.)

$25\ \%$ dazu rechnen

Um $25\ \%$ zu $A_{\mathrm{A_2 B_2 C}}$ dazuzurechnen, kannst du entweder

• $25\ \%$ von $A_{\mathrm{A_2 B_2 C}}$ ausrechnen und dann zu $A_{\mathrm{A_2 B_2 C}}$ addieren,

oder

• gleich $100\ \%+25\ \%=125\ \%$ von $A_{\mathrm{A_2 B_2 C}}$ berechnen.

$125\ \%$ von $A_{\mathrm{A_2 B_2 C}}$ kannst du mit den Formeln zur Prozentrechnung oder mit dem Dreisatz berechnen. In jedem Fall erhältst du:

$\dfrac{125\cdot A_{\mathrm{A_2 B_2 C}}}{100}= 1{,}25 \cdot A(50°)\approx 14{,}57 \, \mathrm{cm^2}$

Anmerkung: Wenn du mit dem gerundeten Ergebnis $11{,}66\, \mathrm{cm^2}$ für $A(50°)$ gerechnet hast, erhältst du jetzt nach Rundung $14{,}58\, \mathrm{cm^2}$.

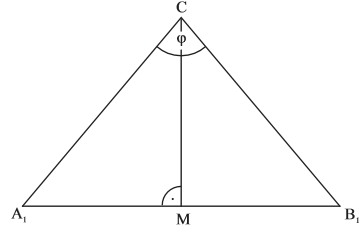
Winkel $\varphi$ ausrechnen

Der gesuchte Winkel $\varphi$ muss gerade so groß sein, dass sich der gewünschte Flächeninhalt ergibt:

Setze daher die "allgemeine" Formel $A(\varphi)=25\cdot \tan\frac{\varphi}{2}\ \mathrm{cm^2}$ gleich mit dem Wert, den die Fläche haben soll und löse nach $\varphi$ auf.

$25\cdot \tan\frac{\varphi}{2}\ \mathrm{cm^2}=14{,}57 \, \mathrm{cm^2}$

So sieht die Gleichung aus, wenn du das gerundete Ergebnis verwendest. Teile durch $25$

$\tan\frac{\varphi}{2}\ \mathrm{cm^2}=\displaystyle\frac{14{,}57 \, \mathrm{cm^2}} {25}$

Wende $\tan^{-1}$ an. $\mathrm{cm^2}$ kannst du weglassen, weil es auf beiden Seiten steht.

$\displaystyle\frac{\varphi}{2}\ =\displaystyle \tan^{-1}\left(\frac{14{,}57}{25}\right)$

Multipliziere mit $2$

$\displaystyle\varphi\ =\displaystyle\tan^{-1}\left(\frac{14{,}57}{25}\right)\cdot 2 = 60{,}47 °$

Wenn du statt des gerundeten Wertes $14{,}57$ $\mathrm{ cm^2}$ den originalen Wert einsetzt, erhältst du das Ergebnis in diesem Fall das gleiche Ergebnis $60{,}47°$.