In einem kartesischen Koordinatensystem legen die Punkte , und das Dreieck ABC fest, das in der Ebene liegt.
Bestimmen Sie den Flächeninhalt des Dreiecks ABC. (3 BE)
Das Dreieck ABC stellt modellhaft einen Spiegel dar. Der Punkt gibt im Modell die Position einer Lichtquelle an, von der ein Lichtstrahl ausgeht.
Die Richtung dieses Lichtstrahls wird im Modell durch den Vektor beschrieben.
Geben Sie eine Gleichung der Geraden an, entlang derer der Lichtstrahl im Modell verläuft. Bestimmen Sie die Koordinaten des Punkts , in dem g die Ebene schneidet, und begründen Sie, dass der Lichtstrahl auf dem dreieckigen Spiegel auftrifft. (5 BE)
(zur Kontrolle: )
Der einfallende Lichtstrahl wird in demjenigen Punkt des Spiegels reflektiert, der im Modell durch den Punkt dargestellt wird. Der reflektierte Lichtstrahl geht für einen Beobachter scheinbar von einer Lichtquelle aus, deren Position im Modell durch den Punkt beschrieben wird (vgl. Abbildung).
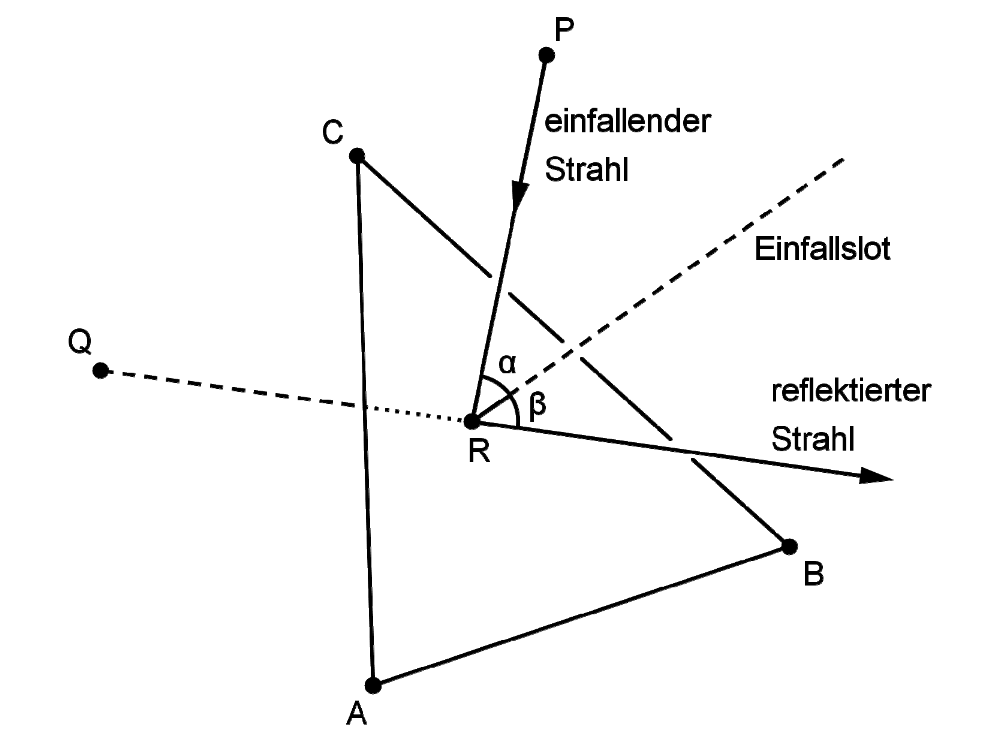
Zeigen Sie, dass die Punkte und bezüglich der Ebene symmetrisch sind. (3 BE)
Das Lot zur Ebene im Punkt wird als Einfallslot bezeichnet.
Die beiden Geraden, entlang derer der einfallende und der reflektierte Lichtstrahl im Modell verlaufen, liegen in einer Ebene . Ermitteln Sie eine Gleichung von in Normalenform. Weisen Sie nach, dass das Einfallslot ebenfalls in der Ebene liegt. (5 BE)
(mögliches Teilergebnis: )
Zeigen Sie, dass die Größe des Winkels β zwischen reflektiertem Licht-strahl und Einfallslot mit der Größe des Winkels α zwischen einfallendem Lichtstrahl und Einfallslot übereinstimmt. (4 BE)
