Lagebeziehungen zwischen 3 Ebenen

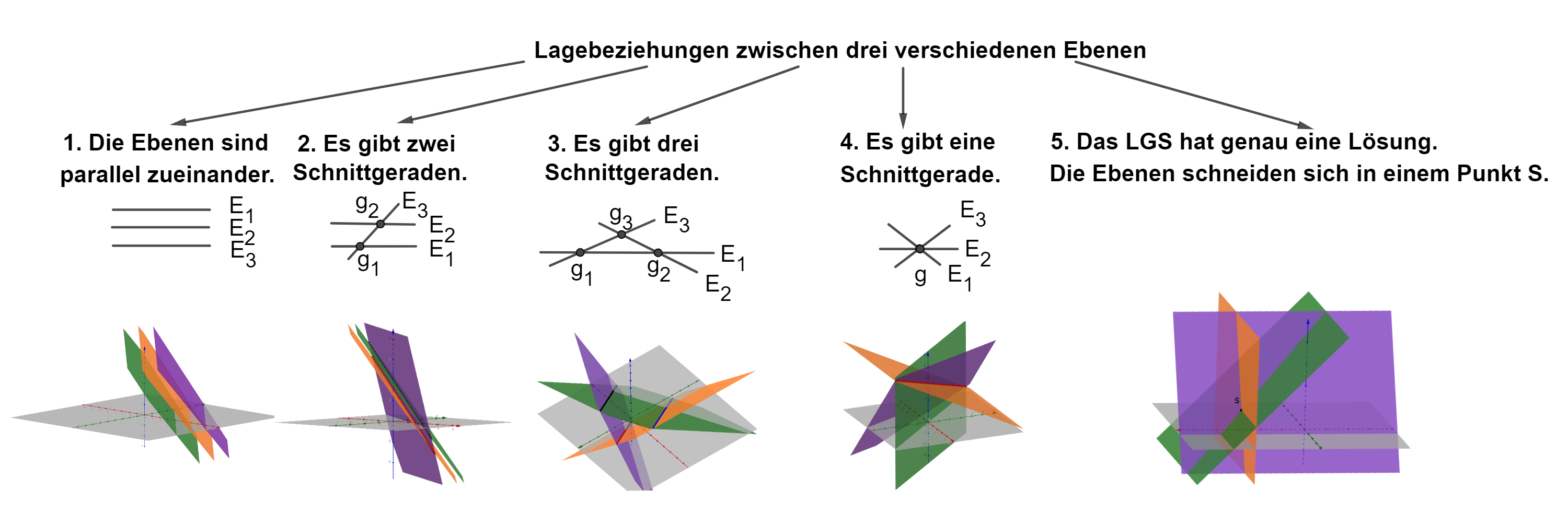
Es gibt insgesamt $5$ Möglichkeiten, wie drei verschiedene Ebenen zueinander liegen können. Diese $5$ Möglichkeiten werden in diesem Artikel vorgestellt.

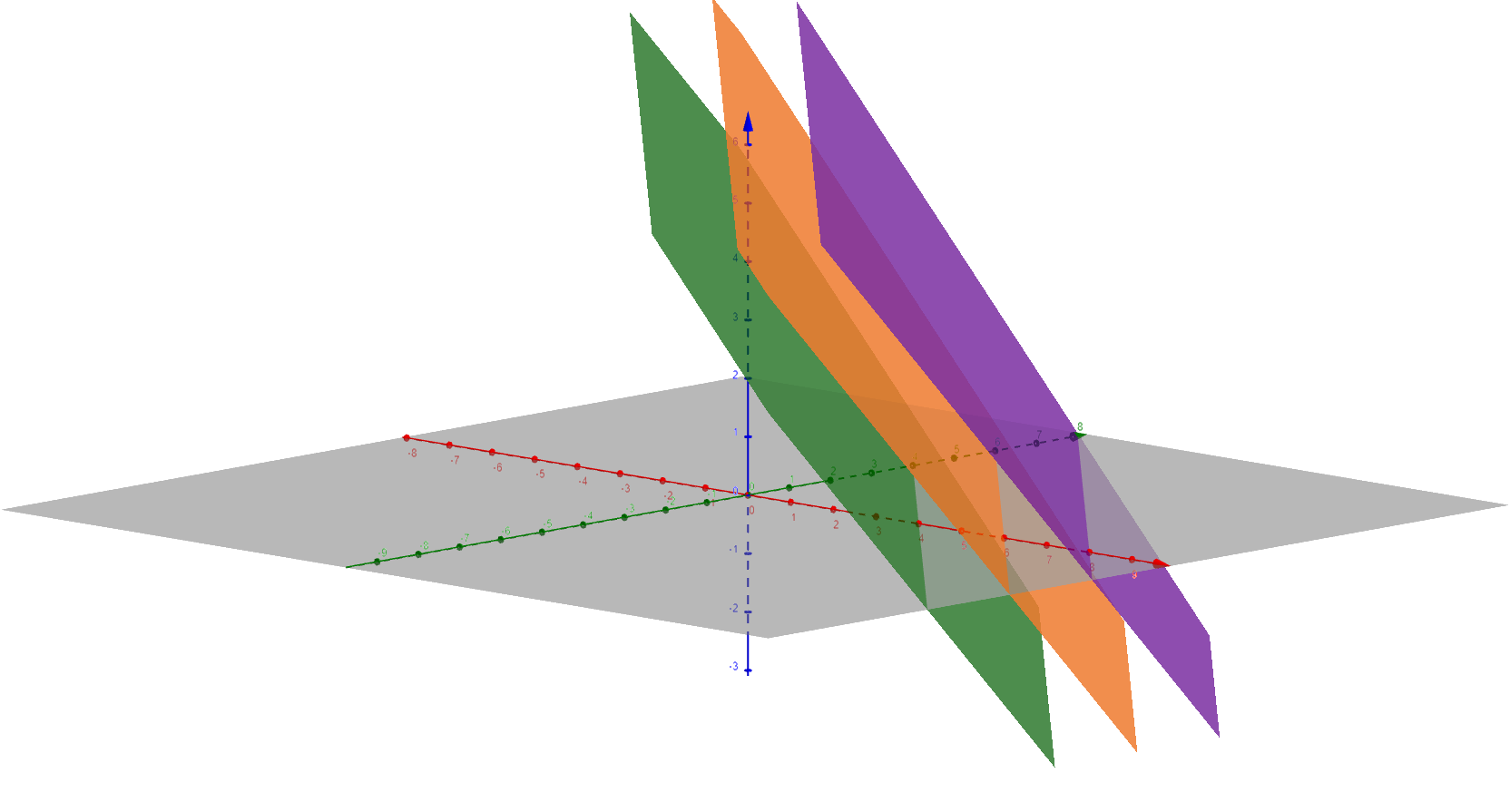
1. Beispiel für drei parallele Ebenen

1.1 Ebenengleichungen

$\begin{array}{ccccc} E_{1} : 1 \cdot x_{1} + 1 \cdot x_{2} + 1 \cdot x_{3} = 4 \\ E_{2} : 1 \cdot x_{1} + 1 \cdot x_{2} + 1 \cdot x_{3} = 6 \\ E_{3} : 1 \cdot x_{1} + 1 \cdot x_{2} + 1 \cdot x_{3} = 8 \end{array}$

1.2 Analyse der Normalenvektoren

Bei drei parallelen Ebenen sind die Normalenvektoren Vielfache voneinander. Die Normalenvektoren sind damit parallel zueinander. Hier gilt: ${\vec{n}}_{E_{1}} = {\vec{n}}_{E_{2}} = {\vec{n}}_{E_{3}}$ . Dies hat zur Folge, dass die Ebenen identisch oder parallel zueinander sind.

Hier gilt: $E_{1} \neq a \cdot E_{2}$ , $E_{1} \neq b \cdot E_{3}$ und $E_{2} \neq c \cdot E_{3}$ . (Die Ebenengleichungen sind keine Vielfache voneinander). Die 3 Ebenen sind (echt) parallel zueinander.

1.3 Schnittgeraden

Parallele Ebenen schneiden sich nicht, d.h. es gibt keine Schnittgeraden.

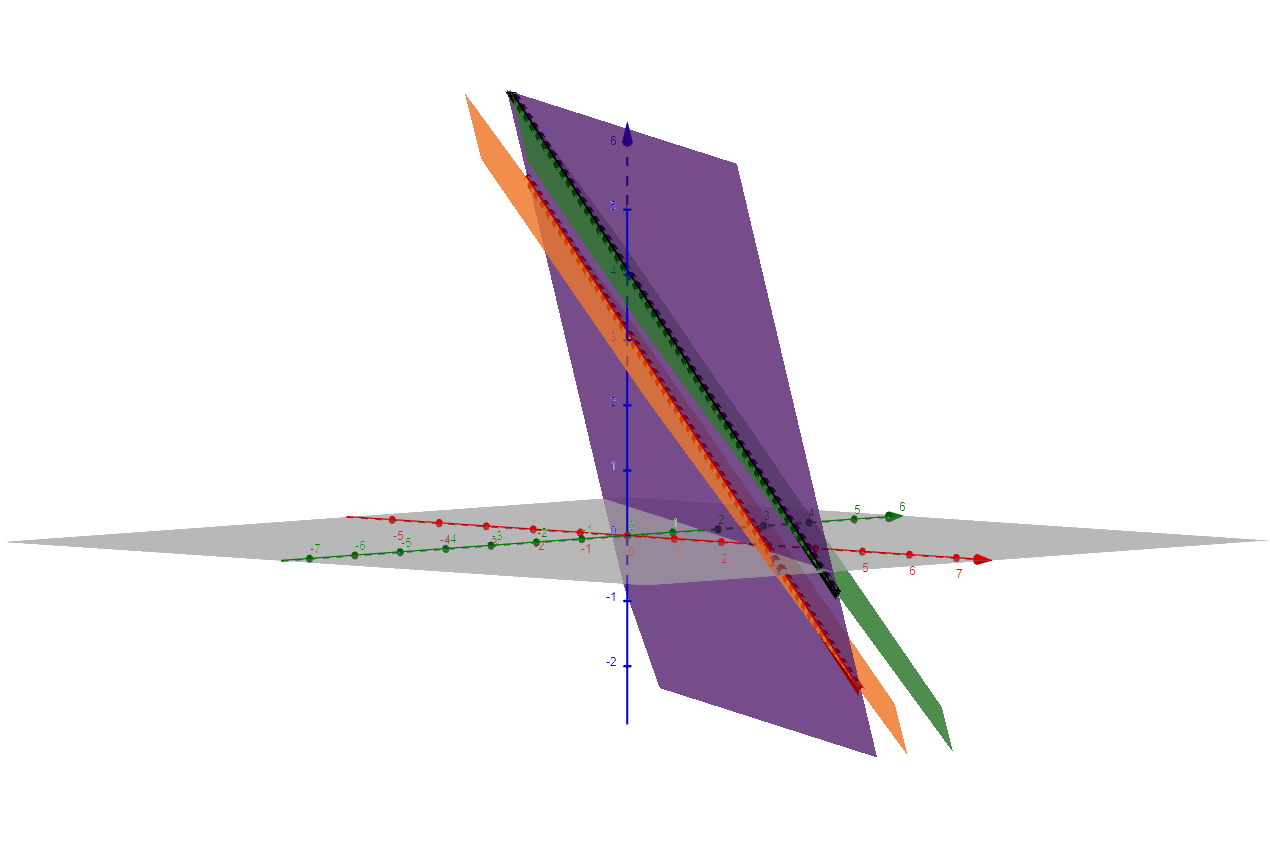
2. Beispiel für zwei parallele Ebenen und eine dazu nicht parallele Ebene.

2 parallele Ebenen und eine dazu nicht parallele Ebene

2.1 Ebenengleichungen

$\begin{array}{ccccc} E_{1} : 1 \cdot x_{1} + 1 \cdot x_{2} + 1 \cdot x_{3} = 4 \\ E_{2} : 2 \cdot x_{1} + 2 \cdot x_{2} + 2 \cdot x_{3} = 6 \\ E_{3} : 2 \cdot x_{1} + 3 \cdot x_{2} + 1 \cdot x_{3} = 5 \end{array}$

2.2 Analyse der Normalenvektoren

Es gilt hier: ${\vec{n}}_{E_{2}} = 2 \cdot {\vec{n}}_{E_{1}}$ . Die beiden Normalenvektoren sind kollinear (parallel).

Außerdem ist $E_{2} \neq 2 \cdot E_{1}$ , d.h. die Ebene $E_{1}$ ist (echt) parallel zu $E_{2}$ .

$E_{3}$ ist nicht parallel zu $E_{1}$ bzw. $E_{2}$ , denn ${\vec{n}}_{E_{3}} \neq k_{1} \cdot {\vec{n}}_{E_{1}}$ und ${\vec{n}}_{E_{3}} \neq k_{2} \cdot {\vec{n}}_{E_{2}}$ .

2.3 Schnittgeraden

Die beiden parallelen Ebenen $E_{1}$ und $E_{2}$ werden von $E_{3}$ geschnitten, d.h. es gibt $2$ verschiedene Schnittgeraden.

$E_{1} \cap E_{3} = g_{1} : \vec{x} = (\begin{array}{c} 1 \\ 0 \\ 3 \end{array}) + r \cdot (\begin{array}{c} - 2 \\ 1 \\ 1 \end{array})$ (schwarze Gerade in der Abbildung)

$E_{2} \cap E_{3} = g_{2} : \vec{x} = (\begin{array}{c} 4 \\ - 1 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 2 \\ 1 \\ 1 \end{array})$ (rote Gerade in der Abbildung)

Beide Schnittgeraden haben den gleichen Richtungsvektor. Sie sind also parallel zueinander.

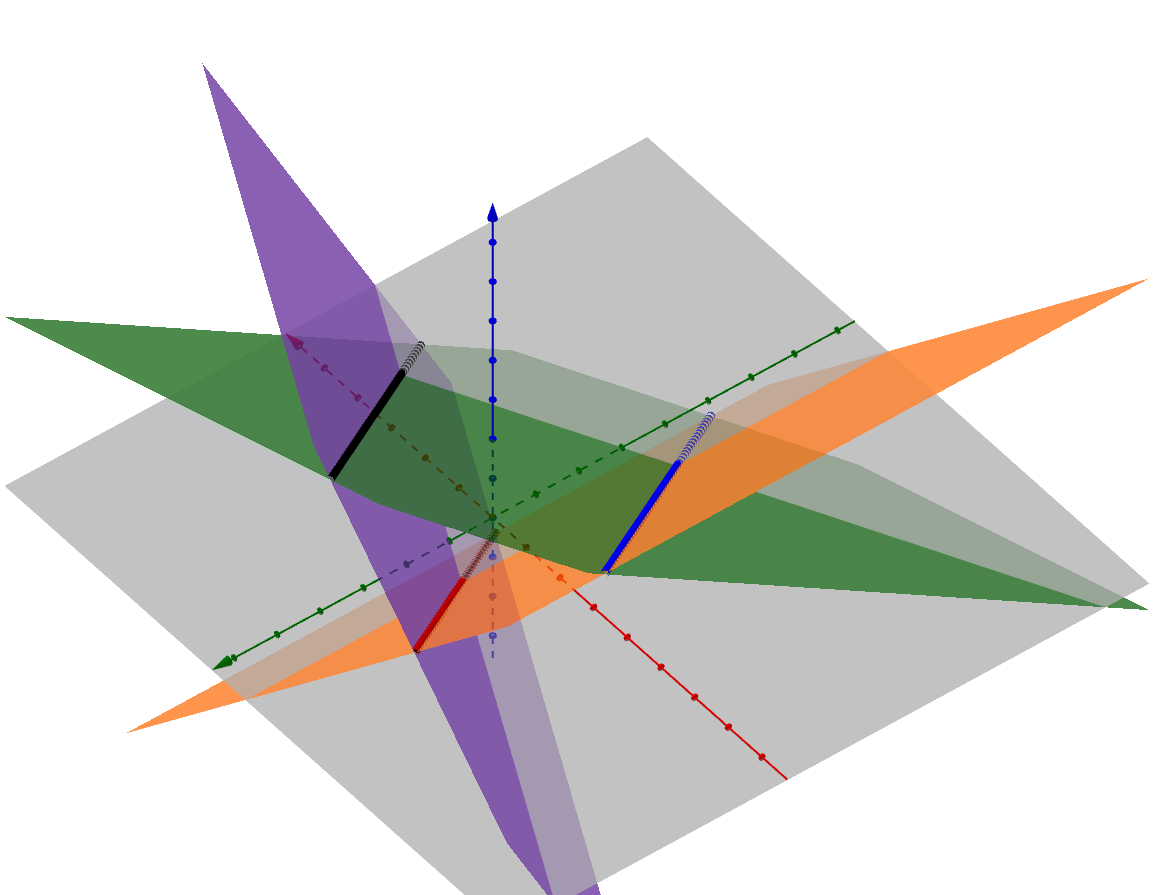
3. Beispiel für drei nicht zueinander parallele Ebenen mit drei Schnittgeraden

3.1 Ebenengleichungen

$\begin{array}{ccccc} E_{1} : 1 \cdot x_{1} - 2 \cdot x_{2} + 3 \cdot x_{3} = 6 \\ E_{2} : 1 \cdot x_{1} + 2 \cdot x_{2} - 1 \cdot x_{3} = 2 \\ E_{3} : 1 \cdot x_{1} + 0 \cdot x_{2} + 1 \cdot x_{3} = - 1 \end{array}$

3.2 Analyse der Normalenvektoren

Die Normalenvektoren der 3 Ebenen sind keine Vielfache voneinander:

${\vec{n}}_{E_{1}} \neq k_{1} \cdot {\vec{n}}_{E_{2}}$ , ${\vec{n}}_{E_{1}} \neq k_{2} \cdot {\vec{n}}_{E_{3}}$ und ${\vec{n}}_{E_{2}} \neq k_{3} \cdot {\vec{n}}_{E_{3}}$

In diesem Fall stellt man fest, dass die drei Normalenvektoren komplanar sind.

${\vec{n}}_{E_{1}} = (\begin{array}{c} 1 \\ - 2 \\ 3 \end{array})$ , ${\vec{n}}_{E_{2}} = (\begin{array}{c} 1 \\ 2 \\ - 1 \end{array})$ , ${\vec{n}}_{E_{3}} = (\begin{array}{c} 1 \\ 0 \\ 1 \end{array})$

Der Normalenvektor ${\vec{n}}_{E_{3}}$ der Ebene $E_{3}$ ist als Linearkombination der beiden anderen Normalenvektoren ${\vec{n}}_{E_{1}}$ und ${\vec{n}}_{E_{2}}$ darstellbar: ${\vec{n}}_{E_{3}} = \frac{1}{2} \cdot {\vec{n}}_{E_{1}} + \frac{1}{2} \cdot {\vec{n}}_{E_{2}}$ .

Damit sind die drei Normalenvektoren linear abhängig. Sie sind komplanar, d.h. sie liegen in einer Ebene.

3.3 Schnittgeraden

Jede Ebene schneidet sich mit den beiden anderen Ebenen, d.h. es gibt 3 verschiedene Schnittgeraden.

$E_{1} \cap E_{2} = g_{1} : \vec{x} = (\begin{array}{c} 4 \\ - 1 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 1 \end{array})$ (schwarze Gerade in der Abbildung)

$E_{2} \cap E_{3} = g_{2} : \vec{x} = (\begin{array}{c} - 1 \\ 1,5 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 1 \end{array})$ (rote Gerade in der Abbildung)

$E_{1} \cap E_{3} = g_{3} : \vec{x} = (\begin{array}{c} - 1 \\ - 3,5 \\ 0 \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 1 \end{array})$ (blaue Gerade in der Abbildung)

Alle drei Schnittgeraden haben den gleichen Richtungsvektor. Sie sind also parallel zueinander.

3.4 Lösung des linearen Gleichungssystems (LGS)

Wird das LGS mit dem Gaußverfahren gelöst, erhältst du in der letzten Zeile der erweiterten Koeffizientenmatrix folgenden Ausdruck: $(0 0 0 | 10)$ .

Ausführlich geschrieben lautet diese Zeile: $0 \cdot x_{1} + 0 \cdot x_{2} + 0 \cdot x_{3} = 10$ .

Diese Gleichung hat keine Lösung, d.h. das LGS hat keine Lösung. Es gibt keinen gemeinsamen Punkt und keine gemeinsame Gerade für die $3$ Ebenen. Allerdings existieren, wie oben gezeigt, drei verschiedene Schnittgeraden.

4. Beispiel für drei verschiedene Ebenen mit einer Schnittgeraden

4.1 Ebenengleichungen

$\begin{array}{ccccc} E_{1} : 1 \cdot x_{1} + 1 \cdot x_{2} + 0 \cdot x_{3} = 0 \\ E_{2} : 2 \cdot x_{1} + 1 \cdot x_{2} - 2 \cdot x_{3} = - 7 \\ E_{3} : 0 \cdot x_{1} + 1 \cdot x_{2} + 2 \cdot x_{3} = 7 \end{array}$

4.2 Analyse der Normalenvektoren

Die Normalenvektoren der 3 Ebenen sind keine Vielfache voneinander:

${\vec{n}}_{E_{1}} \neq k_{1} \cdot {\vec{n}}_{E_{2}}$ , ${\vec{n}}_{E_{1}} \neq k_{2} \cdot {\vec{n}}_{E_{3}}$ und ${\vec{n}}_{E_{2}} \neq k_{3} \cdot {\vec{n}}_{E_{3}}$

In diesem Fall stellt man fest, dass die drei Normalenvektoren komplanar sind.

${\vec{n}}_{E_{1}} = (\begin{array}{c} 1 \\ 1 \\ 0 \end{array})$ , ${\vec{n}}_{E_{2}} = (\begin{array}{c} 2 \\ 1 \\ - 2 \end{array})$ , ${\vec{n}}_{E_{3}} = (\begin{array}{c} 0 \\ 1 \\ 2 \end{array})$

Der Normalenvektor ${\vec{n}}_{E_{3}}$ der Ebene $E_{3}$ ist als Linearkombination der beiden anderen Normalenvektoren ${\vec{n}}_{E_{1}}$ und ${\vec{n}}_{E_{2}}$ darstellbar: ${\vec{n}}_{E_{3}} = 2 \cdot {\vec{n}}_{E_{1}} - 1 \cdot {\vec{n}}_{E_{2}}$ .

Damit sind die drei Normalenvektoren linear abhängig. Sie sind komplanar, d.h. sie liegen in einer Ebene.

4.3 Schnittgeraden

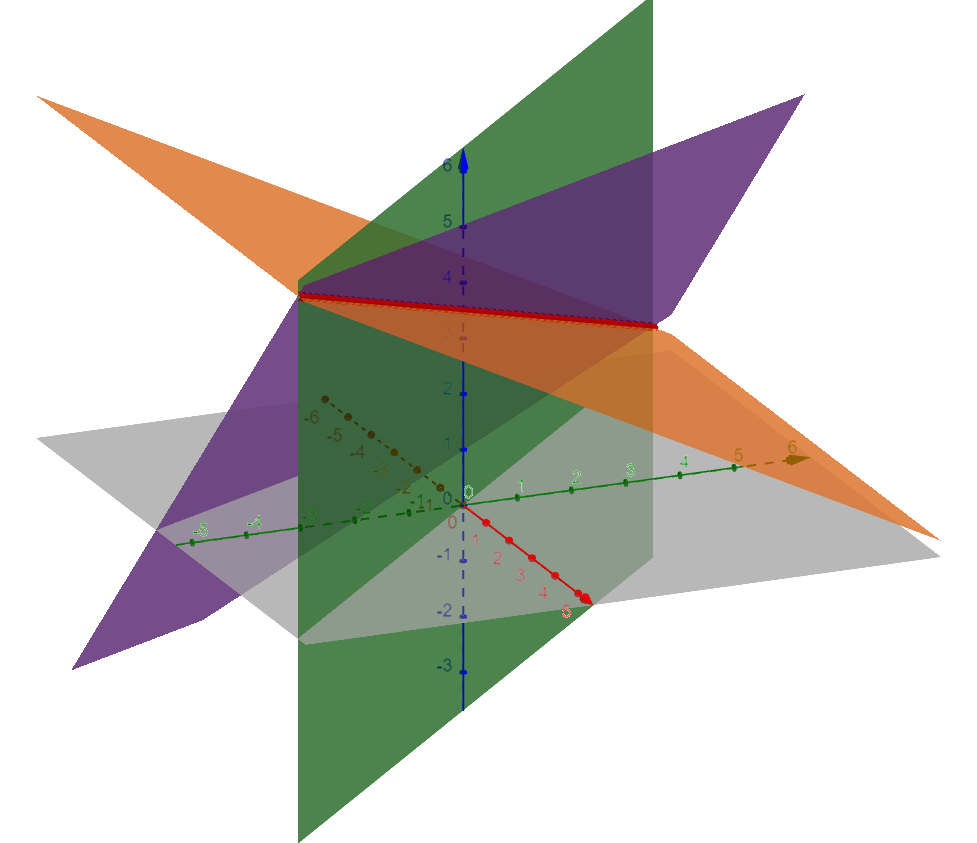
In diesem Fall schneiden sich alle drei Ebenen in einer Geraden. Die Schnittgerade (rot eingezeichnet) hat die Gleichung:

$g : \vec{x} = (\begin{array}{c} 0 \\ 0 \\ 3,5 \end{array}) + r \cdot (\begin{array}{c} 2 \\ - 2 \\ 1 \end{array})$

4.4 Lösung des linearen Gleichungssystems (LGS)

Wird das LGS mit dem Gaußverfahren gelöst, erhältst du in der letzten Zeile der erweiterten Koeffizientenmatrix folgenden Ausdruck: $(0 0 0 | 0)$ .

Ausführlich geschrieben lautet diese Zeile: $0 \cdot x_{1} + 0 \cdot x_{2} + 0 \cdot x_{3} = 0$ .

Diese Gleichung hat unendlich viele Lösungen, d.h. das LGS hat unendlich viele Lösungen.

Da in diesem LGS keine identischen Ebenen auftreten, bedeutet das, alle Lösungen des LGS liegen auf einer Geraden. Die $3$ Ebenen haben eine gemeinsame Schnittgerade.

5. Beispiel für drei verschiedene Ebenen mit einem Schnittpunkt

5.1 Ebenengleichungen

$\begin{array}{ccccc} E_{1} : 1 \cdot x_{1} + 0 \cdot x_{2} + 0 \cdot x_{3} = 3 \\ E_{2} : 0 \cdot x_{1} + 2 \cdot x_{2} + 1 \cdot x_{3} = 2 \\ E_{3} : 1 \cdot x_{1} + 0 \cdot x_{2} + 1 \cdot x_{3} = 4 \end{array}$

5.2 Analyse der Normalenvektoren

Die Normalenvektoren der 3 Ebenen sind keine Vielfache voneinander:

${\vec{n}}_{E_{1}} \neq k_{1} \cdot {\vec{n}}_{E_{2}}$ , ${\vec{n}}_{E_{1}} \neq k_{2} \cdot {\vec{n}}_{E_{3}}$ und ${\vec{n}}_{E_{2}} \neq k_{3} \cdot {\vec{n}}_{E_{3}}$

Die Normalenvektoren sind linear unabhängig, denn die Gleichung $r \cdot {\vec{n}}_{E_{1}} + s \cdot {\vec{n}}_{E_{2}} + t \cdot {\vec{n}}_{E_{3}} = \vec{0}$ ist nur für $r = s = t = 0$ erfüllt.

5.3 Schnittgeraden

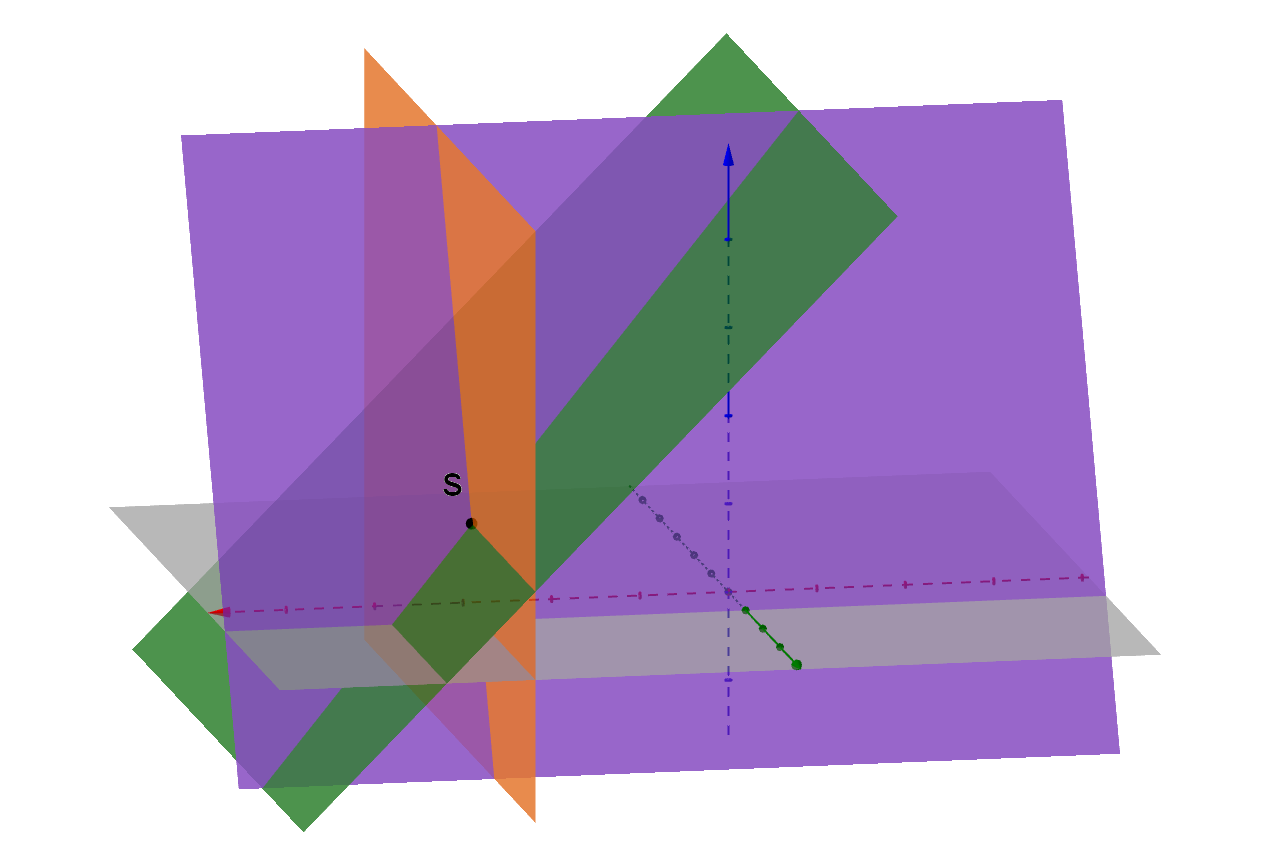
Jede Ebene schneidet sich mit den beiden anderen Ebenen, d.h. es gibt $3$ verschiedene Schnittgeraden. Diese $3$ Schnittgeraden wiederum schneiden sich in einem Punkt $S$ . Dieser Punkt ist der Schnittpunkt der $3$ Ebenen. (Die Gleichungen der $3$ Schnittgeraden sind hier nicht von Interesse.)

5.4 Lösung des linearen Gleichungssystems (LGS)

Wird das LGS mit dem Gaußverfahren gelöst, erhältst du in der letzten Zeile der erweiterten Koeffizientenmatrix folgenden Ausdruck: $(0 0 1 | 1)$ .

Ausführlich geschrieben lautet diese Zeile: $0 \cdot x_{1} + 0 \cdot x_{2} + 1 \cdot x_{3} = 1$ .

Somit ist $x_{3} = 1$ . Die anderen Werte $x_{1} = 3$ und $x_{2} = \frac{1}{2}$ ergeben sich aus dem Gleichungssystem. Das LGS hat eine eindeutige Lösung: $𝕃 = {(3 | \frac{1}{2} | 1)}$

Die $3$ Ebenen schneiden sich in einem Punkt $S (3 | \frac{1}{2} | 1)$ .

Übungsaufgaben Lagebeziehungen zwischen 3 Ebenen

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Lagebeziehung dreier Ebenen

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Lagebeziehungen zwischen 3 Ebenen

1. Beispiel für drei parallele Ebenen

1.1 Ebenengleichungen

1.2 Analyse der Normalenvektoren

1.3 Schnittgeraden

2. Beispiel für zwei parallele Ebenen und eine dazu nicht parallele Ebene.

2.1 Ebenengleichungen

E1:1⋅x1+1⋅x2+1⋅x3=4E2:2⋅x1+2⋅x2+2⋅x3=6E3:2⋅x1+3⋅x2+1⋅x3=5

2.2 Analyse der Normalenvektoren

2.3 Schnittgeraden

3. Beispiel für drei nicht zueinander parallele Ebenen mit drei Schnittgeraden

3.1 Ebenengleichungen

3.2 Analyse der Normalenvektoren

3.3 Schnittgeraden

3.4 Lösung des linearen Gleichungssystems (LGS)

4. Beispiel für drei verschiedene Ebenen mit einer Schnittgeraden

4.1 Ebenengleichungen

4.2 Analyse der Normalenvektoren

4.3 Schnittgeraden

4.4 Lösung des linearen Gleichungssystems (LGS)

5. Beispiel für drei verschiedene Ebenen mit einem Schnittpunkt

5.1 Ebenengleichungen

5.2 Analyse der Normalenvektoren

5.3 Schnittgeraden

5.4 Lösung des linearen Gleichungssystems (LGS)

Übungsaufgaben Lagebeziehungen zwischen 3 Ebenen

$\begin{array}{ccccc} E_{1} : 1 \cdot x_{1} + 1 \cdot x_{2} + 1 \cdot x_{3} = 4 \\ E_{2} : 2 \cdot x_{1} + 2 \cdot x_{2} + 2 \cdot x_{3} = 6 \\ E_{3} : 2 \cdot x_{1} + 3 \cdot x_{2} + 1 \cdot x_{3} = 5 \end{array}$