Aufgabe 1C
Ein ICE fährt bis 15: 00 Uhr mit konstanter Geschwindigkeit. Von 15: 00 Uhr bis 15: 02 Uhr nimmt seine Geschwindigkeit ab. Ab 15: 02 Uhr fährt der ICE wieder mit konstanter Geschwindigkeit.
Die Geschwindigkeit von 15: 00 Uhr bis 15: 02 Uhr wird mithilfe der in definierten Funktion mit beschrieben.
Dabei ist die seit 15: 00 Uhr vergangene Zeit in Minuten und die Geschwindigkeit in Kilometer pro Stunde. Abbildung 1 veranschaulicht den Sachverhalt.
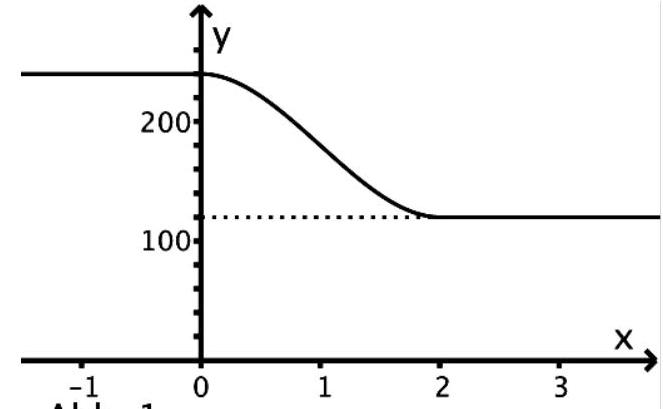
Bestimmen Sie die Geschwindigkeit, die der ICE eine halbe Minute nach 15: 00 Uhr hat.
Zeigen Sie, dass die Geschwindigkeit in der ersten halben Minute nach 15: 00 Uhr um einen kleineren Betrag abnimmt als in der darauf folgenden halben Minute. (4 BE)
Bestimmen Sie die Länge des Zeitraumes, in dem die Geschwindigkeit höchstens 200 aber mindestens 150 Kilometer pro Stunde beträgt. (3 BE)
Geben Sie mögliche Werte und an, sodass gilt: . Deuten Sie die Aussage im Sachzusammenhang. (3 BE)
Ermitteln Sie den Zeitpunkt, zu dem die Geschwindigkeit am stärksten abnimmt.
(3 BE)
Bestimmen Sie einen Zeitraum, der frühestens um 14:59 Uhr beginnt und spätestens um 15: 03 Uhr endet, in dem der ICE eine Strecke mit einer Länge von genau zurücklegt.
(5 BE)
Untersuchen Sie, ob folgende Aussage richtig ist: (6 BE)
Wenn sich die Abnahme der Geschwindigkeit von 15: 01 Uhr an nicht mehr verändern würde, dann käme der ICE von diesem Zeitpunkt an nach drei Kilometern zum Stehen.
Betrachtet wird die in definierte Funktion mit mit .
Die Punkte und sind direkt aufeinanderfolgende Extrempunkte des Graphen von .
Bestimmen Sie die passenden Werte von und . (5 BE)
[Zur Kontrolle: ]
Berechnen Sie den Wert des Terms . Beschreiben Sie mithilfe der Abbildung 2, wie man zu diesem Wert mit geometrischen Überlegungen gelangen kann. (6 BE)
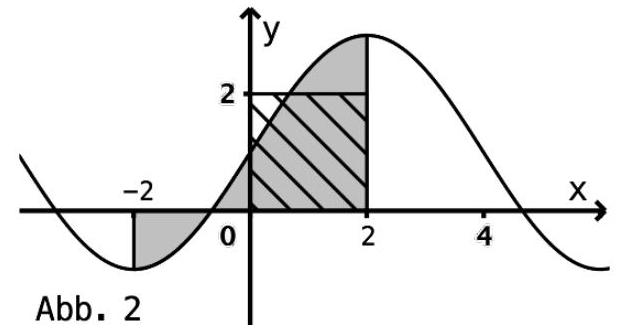
Die Punkte des Graphen von mit der -Koordinate 1 sind die Wendepunkte des Graphen. Die -Koordinate der Wendepunkte ist ganzzahlig und ein Vielfaches von 4. Die Steigung des Graphen von in jedem seiner Wendepunkte ist entweder oder .
Für jeden Wendepunkt des Graphen von wird die Gerade betrachtet, die durch diesen Wendepunkt und den Punkt verläuft.
Untersuchen Sie, ob eine dieser Geraden im jeweiligen Wendepunkt Tangente an den
Graphen von ist. (5 BE)
Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen


