Wahlteil - GTR - lernen mit Serlo!

Aufgabe 1B

Ein mit Wasser befülltes Glas wird aus einem Kühlschrank genommen. Die anschließende Entwicklung der Wassertemperatur infolge der höheren Raumtemperatur lässt sich mithilfe der in $\mathbb{R}$ definierten Funktion $𝑓$ mit $𝑓(𝑡) = 25 − 20𝑒^{−0{,}014⋅𝑡}$ modellhaft beschreiben. Dabei ist $t$ die Zeit in Minuten, die seit der Entnahme aus dem Kühlschrank vergangen ist, und $f (t)$ die Wassertemperatur in $^\circ C$ . Die Raumtemperatur beträgt konstant $25^\circ C$ .

Geben Sie die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an.
Bestimmen Sie den Zeitpunkt, zu dem die Wassertemperatur $12^\circ C$ beträgt. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Gib die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an.
Berechne $f (0)$ :
$f (0) = 25 - 20 = 5$
Die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank beträgt $5^\circ C$ .
Bestimme den Zeitpunkt, zu dem die Wassertemperatur $12^\circ C$ beträgt
$f (t) = 12$ , liefert die Lösung $t\approx30{,}8$ .
Das Wasser hat rund $31$ Minuten nach der Entnahme eine Temperatur von $12^\circ C$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Berechne $f (0)$ .
Teil 2
$\text{Löse}(f(t)=12)$ .
Berechnen Sie die Werte der folgenden Terme und interpretieren Sie diese im Sachzusammenhang: [6 BE]
1. $f^{'} (30)$
2. $\dfrac{f(30)−f(0)}{30−0}$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Die mittlere Änderungsrate – Einführung der Ableitung
Berechne die Werte der folgenden Terme und interpretiere diese im Sachzusammenhang
$\mathrm{(I)}\;$ : $f'(30) \approx 0{,}18$ $\\$
$f^{'} (30)$ beschreibt die momentane Änderungsrate der Wassertemperatur $30$ Minuten nach Entnahme in Grad pro Minute.
$\mathrm{(II)}\;$ : $\dfrac{f(30)−f(0)}{30−0}\approx0{,}23$ $\\$
$\dfrac{f(30)−f(0)}{30−0}$ beschreibt die mittlere Änderungsrate der Wassertemperatur innerhalb der ersten $30$ Minuten in Grad pro Minute.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Berechne $f^{'} (30)$ . Die erste Ableitung entspricht der momentanen Änderungsrate.
Berechne $\dfrac{f(30)−f(0)}{30−0}$ . Sekantensteigung oder mittlere Änderungsrate.
Gegeben ist die in $R$ definierte Funktion ℎ mit $h (𝑥) = (1 - 𝑥^{2}) \cdot 𝑒^{𝑥} ℎ(𝑥) = (1 − 𝑥^2) ⋅ 𝑒^𝑥$ .
Der Graph von ℎ wird mit $𝐺_{h} 𝐺_ℎ$ bezeichnet.
Ohne Nachweis können Sie verwenden:
$h^{'} (𝑥) = (- 𝑥^{2} - 2 𝑥 + 1) \cdot 𝑒^{x} ℎ'(𝑥) = (−𝑥^2 − 2𝑥 + 1) ⋅ 𝑒^x$
Begründen Sie anhand des Funktionsterms von $h ℎ$ , dass der Funktionswert $h (𝑥) ℎ(𝑥)$ nur für $- 1 < 𝑥 < 1$ positiv ist. [3 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: e-Funktion
Begründe anhand des Funktionsterms, dass der Funktionswert $h (x)$ nur für $- 1 < x < 1$ positiv ist
Die Funktion hat die beiden Nullstellen $x_{1} = - 1$ und $x_{2} = 1$ .
Betrachte den Funktionsterm: $(1 - x^{2}) \cdot e^{x} (1 − x^2) ⋅ e^x$
$e^{x}$ ist für alle $x$ größer null.
Der Term $(1 - x^{2})$ ist für $- 1 < x < + 1$ ebenfalls größer null, sodass das Produkt aus den beiden Termen $e^{x}$ und $(1 - x^{2})$ ebenfalls größer null ist.
(Für $x$ -Werte außerhalb des Intervalls $] - 1; 1 [$ ist der Term $(1 - x^{2})$ kleiner null.)
Damit ist $h (x)$ nur für $- 1 < x < 1$ positiv.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Bestimme die Nullstellen der Funktion $f$ .
Betrachte die beiden Terme $(1 - x^{2})$ und $e^{x}$ und entscheide, für welche x-Werte die Terme größer oder kleiner null sind.
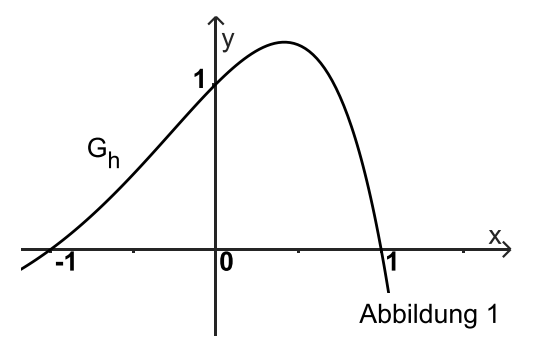
Die Gerade 𝑢 ist die Tangente an $𝐺_{h} 𝐺_ℎ$ im Punkt $(0 ∣ 1)$ . Es gibt genau eine Tangente 𝑣 an $𝐺_{h} 𝐺_ℎ$ , die zu $𝑢$ senkrecht ist. Geben Sie die notwendigen Schritte zur Berechnung einer Gleichung von $𝑣$ an und erläutern Sie diese. [6 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Gib die notwendigen Schritte zur Berechnung einer Gleichung von $v$ an und erläutere diese
Die Gerade $u$ ist die Tangente an $G_{h}$ im Punkt $(0 ∣ 1)$ $\;\Rightarrow\;m_u=h'(0)$
Es gibt eine Tangente $v$ an $G_{h}$ , die zu $u$ senkrecht ist $\;\Rightarrow\;m_u\cdot m_v=-1$
Steigung von $v: m_v=-\dfrac{1}{m_u}=-\dfrac{1}{h'(0)}$
Lösen der Gleichung $h'(x)= − \dfrac{1}{h'(0)}$ zur Bestimmung der $x$ -Koordinate $x_{Q}$ des Berührpunkts $Q$ von $G_{h}$ und $v$ .
Bestimmung der $y$ -Koordinate $y_{Q}$ von $Q$ : $y_{Q} = h (x_{Q})$
Bestimmung des $y$ -Achsenabschnitts von $v$ mithilfe der Steigung von $v$ und der Koordinaten von $Q$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Steigung von $m_v=-\dfrac{1}{m_u}=-\dfrac{1}{h'(0)}$
Löse $h'(x)= − \dfrac{1}{h'(0)}$ zur Bestimmung der x-Koordinate $x_{Q}$ des Berührpunkts $Q$ von $G_{h}$ und $v$ .
Berechne $y_{Q} = h (x_{Q})$
Bestimmung des y-Achsenabschnitts von $v$ mithilfe der Steigung von $v$ und der Koordinaten von $Q$ .
In einem der Wendepunkte von $𝐺_{h} 𝐺_ℎ$ ist die Steigung von $𝐺_{h} 𝐺_ℎ$ maximal.
Berechnen Sie die Koordinaten dieses Wendepunktes und den Wert der maximalen
Steigung. [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
Berechne die Koordinaten dieses Wendepunktes
$h^{''} (x) = 0$ $\;\Rightarrow\;$ $x_1 \approx -3{,}73$ und $x_2 \approx -0{,}27$ .
Es gibt zwei Wendestellen $x_{1}$ und $x_{2}$ .
Da $h^{'} (x_{2}) > h^{'} (x_{1})$ , hat $h^{'}$ an der Stelle $x_{2}$ ein Maximum und $h(x_2)\approx 0{,}71$ ist
die zugehörige y-Koordinate $\;\Rightarrow\;WP(-0{,}27|0{,}71)$ .
Berechne den Wert der maximalen Steigung
$h'(x_2)\approx 1{,}12$
Der Wert der maximalen Steigung im Wendepunkt ist rund $1,12$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
$h''(x) = 0\;\Rightarrow\;x_1$ und $x_{2}$ . Vergleiche $h^{'} (x_{1})$ mit $h^{'} (x_{2})$ . Beim größeren Wert liegt das gesuchte Maximum der Steigung. Berechne die dazugehörige y-Koordinate.
Teil 2
Berechne $h^{'} (x_{1})$ oder $h^{'} (x_{2})$ .
Für $0 < 𝑤 < 1$ wird das Dreieck mit den Eckpunkten $(0 ∣ 0)$ , $(𝑤 ∣ 0)$ und $(𝑤 ∣ h (𝑤)) (𝑤|ℎ(𝑤))$ betrachtet. Für einen Wert von $𝑤$ ist der Flächeninhalt des Dreiecks maximal.
Bestimmen Sie den maximalen Flächeninhalt. [5 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Für einen Wert von $w$ ist der Flächeninhalt des Dreiecks maximal
Skizze:
Es ist $A(w)=\dfrac{1}{2}\cdot w\cdot h(w)=\dfrac{1}{2}\cdot w\cdot (1 − w^2) \cdot e^w$
$\text{Löse}(A'(w) = 0)\;\Rightarrow\;$ im Bereich $0 < w < 1$ gibt es die Lösung $w\approx 0{,}68$ .
Der Flächeninhalt des Dreiecks ist maximal für $w\approx 0{,}68$ .
Berechne den maximalen Flächeninhalt
Berechne $A (0,68)$ :
$A(0{,}68)\approx0{,}36$
Der maximale Flächeninhalt beträgt rund $0{,}36\;\text{FE}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Es ist $A(w)=\dfrac{1}{2}\cdot w\cdot h(w)$ . Bestimme $A'(w) = 0\;\Rightarrow\; w_1$
Teil 2
Berechne $A (w_{1})$ .
$𝐺_{h} 𝐺_ℎ$ schließt mit der 𝑥-Achse eine Fläche $𝐴$ ein.
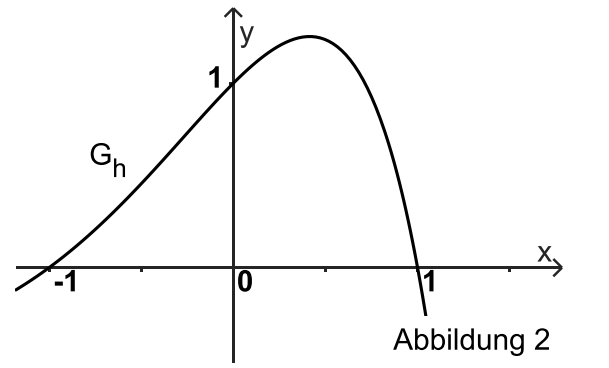
Es gibt genau einen Punkt $𝑃$ auf $𝐺_{h} 𝐺_ℎ$ mit positiver $𝑥$ -Koordinate, sodass die Gerade durch die Punkte $𝑂 (0 ∣ 0)$ und $𝑃$ die Fläche $𝐴$ in zwei Flächenstücke gleichen Inhalts teilt.
Geben Sie eine Gleichung an, mit der die 𝑥-Koordinate von 𝑃 bestimmt werden kann.
Veranschaulichen Sie den Aufbau der Gleichung in Abbildung 2. [7 BE]
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Gib eine Gleichung an, mit der die x-Koordinate von $P$ bestimmt werden kann
Für die Koordinate $x_{P}$ des Punktes $P$ gilt:
Die Hälfte der Fläche, die $G_{h}$ mit der x-Achse einschließt, ist so groß wie die Summe der beiden Flächen $\textcolor{ff6600}{A_1}$ und $\textcolor{660099}{A_2}$ .
$\dfrac{1}{2}\cdot\underbrace{\displaystyle\int_{-1}^1h(x)\;\mathrm{d}x}_{A{\text{gesamt}}}=\textcolor{ff6600}{ \underbrace{\dfrac{1}{2}\cdot x_P\cdot h(x_P)}_{A_1}}+\textcolor{660099}{\underbrace{\displaystyle\int_{x_P}^1h(x)\;\mathrm{d}x}_{A_2}}$

Veranschauliche den Aufbau der Gleichung in Abbildung 2
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Teil 1
Zeichne einen Punkt $P$ auf $G_{h}$ mit positiver x-Koordinate ein. $x_{P}$ ist seine x-Koordinate.
Die Hälfte der Fläche, die $G_{h}$ mit der x-Achse einschließt, ist so groß wie die Summe der Dreiecksfläche $A_{Ox_PP}$ und der Fläche unter $G_{h}$ von $x_{P}$ bis $1$ .
Teil 2
Markiere die unter Teil 1 angegebenen Flächen in der Abbildung 2.

Aufgabe 1B

Gib die Wassertemperatur zum Zeitpunkt der Entnahme aus dem Kühlschrank an.

Bestimme den Zeitpunkt, zu dem die Wassertemperatur 12∘C12^\circ C12∘C beträgt

Hast du eine Frage oder Feedback?

Berechne die Werte der folgenden Terme und interpretiere diese im Sachzusammenhang

Hast du eine Frage oder Feedback?

Begründe anhand des Funktionsterms, dass der Funktionswert h(x)h(x)h(x) nur für −1<x<1−1 < x < 1−1<x<1 positiv ist

Hast du eine Frage oder Feedback?

Gib die notwendigen Schritte zur Berechnung einer Gleichung von vvv an und erläutere diese

Hast du eine Frage oder Feedback?

Berechne die Koordinaten dieses Wendepunktes

Berechne den Wert der maximalen Steigung

Hast du eine Frage oder Feedback?

Für einen Wert von www ist der Flächeninhalt des Dreiecks maximal

Berechne den maximalen Flächeninhalt

Hast du eine Frage oder Feedback?

Gib eine Gleichung an, mit der die x-Koordinate von PPP bestimmt werden kann

Veranschauliche den Aufbau der Gleichung in Abbildung 2

Hast du eine Frage oder Feedback?

Bestimme den Zeitpunkt, zu dem die Wassertemperatur $12^\circ C$ beträgt

Begründe anhand des Funktionsterms, dass der Funktionswert $h (x)$ nur für $- 1 < x < 1$ positiv ist

Gib die notwendigen Schritte zur Berechnung einer Gleichung von $v$ an und erläutere diese

Für einen Wert von $w$ ist der Flächeninhalt des Dreiecks maximal

Gib eine Gleichung an, mit der die x-Koordinate von $P$ bestimmt werden kann