Wahlteil
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
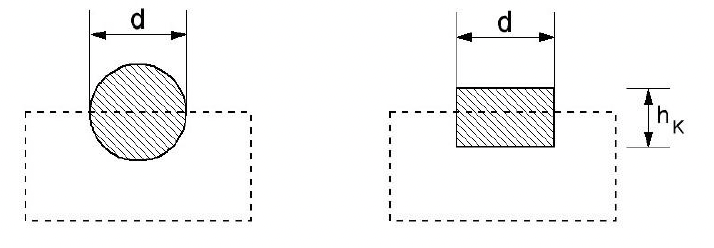
Abgebildet ist ein quaderförmiger Tab für die Spülmaschine. In der Mitte des Tabs befindet sich eine Kugel.

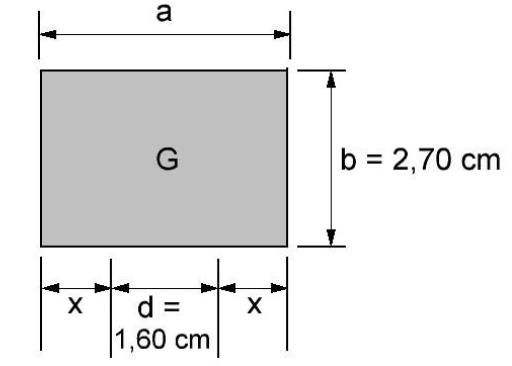
Die Länge beträgt .
Berechne .
[ 1 Pkt ]
Berechne die Grundfläche des Tabs. (Solltest du die Teilaufgabe ) nicht gelöst haben, rechne mit weiter.)
[ 1 Pkt ]
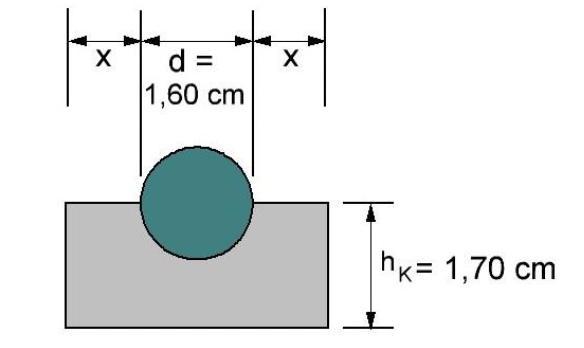
Berechne das Volumen der Kugel.
[ 2Pkte ]
Berechne das Volumen des gesamten Tabs.
(Solltest du die Teilaufgaben ) und ) nicht gelöst haben, rechne mit und weiter.)
[ 3 Pkte ]
Der Hersteller der Tabs plant, die Kugel gegen einen Zylinder mit gleichem Durchmesser und gleichem Volumen auszutauschen.
Berechne die Körperhöhe des Zylinders. (Solltest du die Teilaufgabe ) nicht gelöst haben, rechne mit weiter.)
[ 2 Pkte ]
Ergänze eines der Wörter:
verdoppelt / verdreifacht / vervierfacht / verachtfacht.
Verdoppelt man den Durchmesser der Kugel, dann_______________________ sich ihr Volumen.
[ 1 Pkt ]
- 2
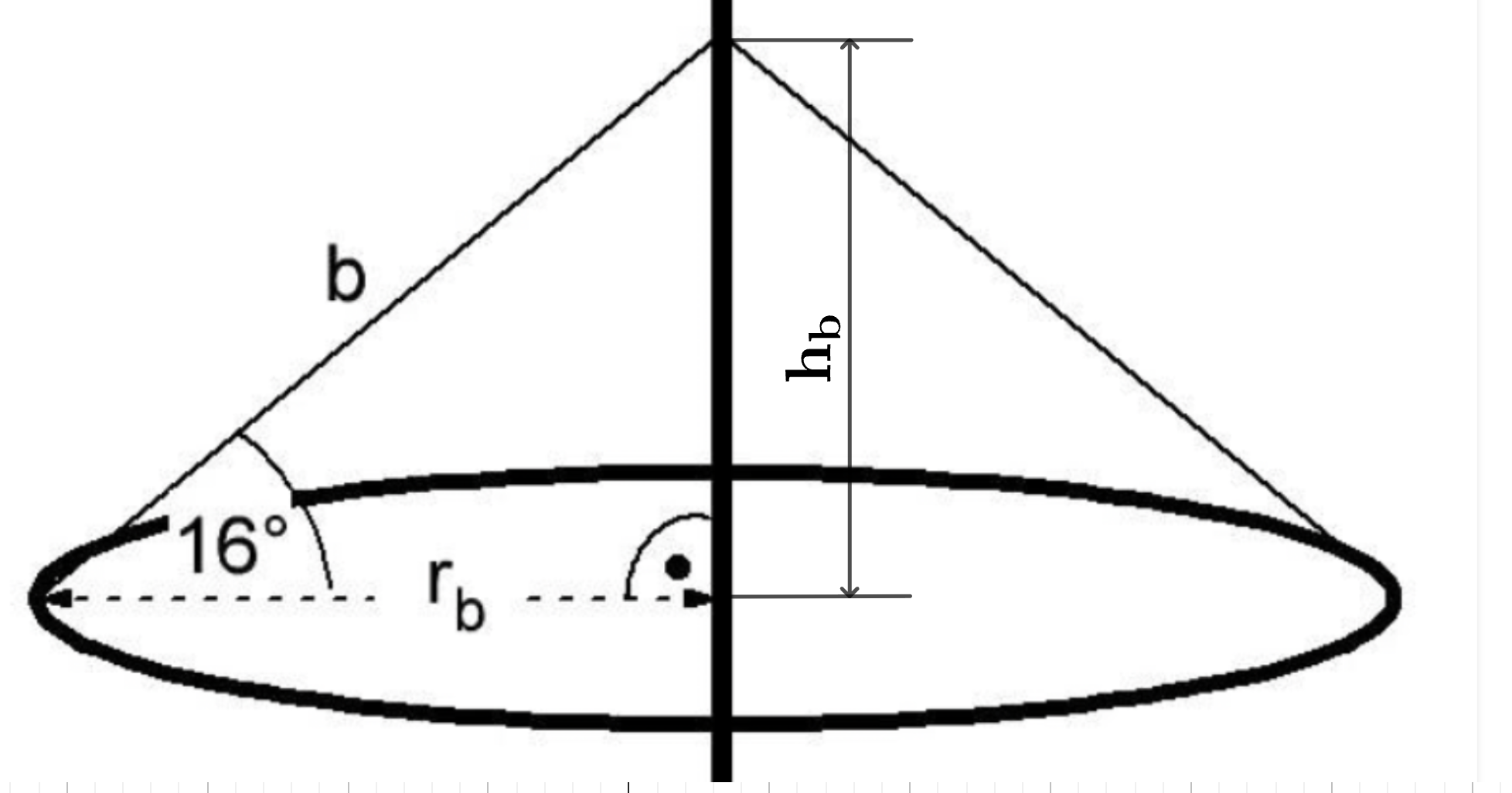
Ein Maibaum besteht oft aus einem Stamm und mehreren ringförmigen Kränzen, die mit Seilen am Stamm befestigt sind.

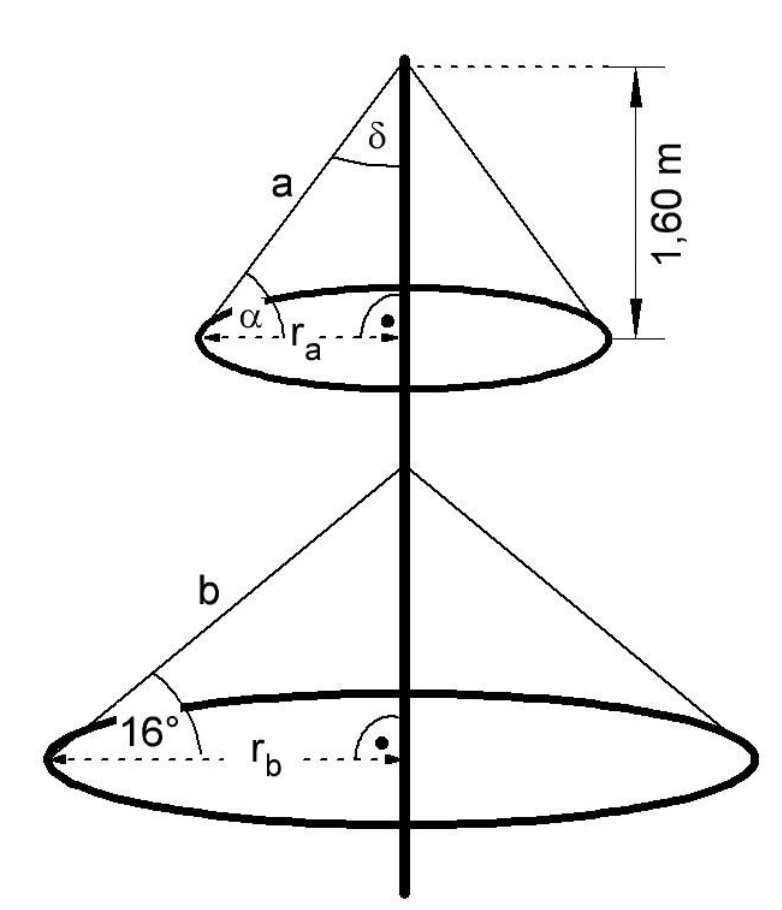
(Skizze nicht maßstäblich)
Der obere Kranz hat einen Radius von .
Berechne den Umfang des oberen Kranzes.
[ 2 Pkt ]
Berechne die Seillänge .
[ 2 Pkt ]
Berechne die Größe des Winkels α.
[ 2 Pkt ]
Bestimme die Größe des Winkels δ.
(Solltest du die Teilaufgabe ) nicht gelöst haben, rechne mit weiter.)
[ 1 Pkt ]
Die Seillänge beträgt .
Berechne den Radius des unteren Kranzes.
[ 2 Pkt ]
Kreuze an:
Wenn der Durchmesser eines Kranzes verdoppelt wird, dann ist sein Umfang anschließend…
[ 1 Pkt ]
- 3
Zwei Würfel sind wie folgt beschriftet:
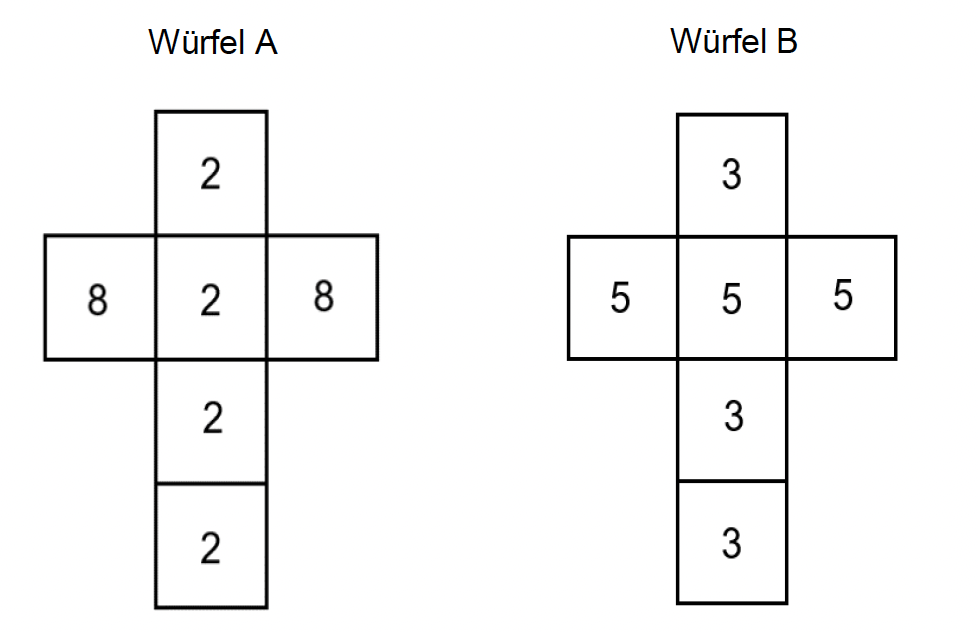
Fülle die Tabelle aus.
[ 2 Pkte ]

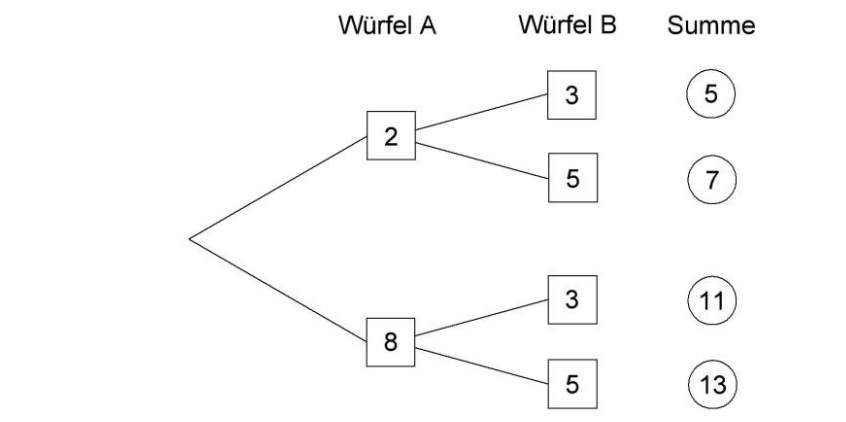
Nun wird mit beiden Würfeln gleichzeitig geworfen.
Die geworfenen Zahlen werden addiert.
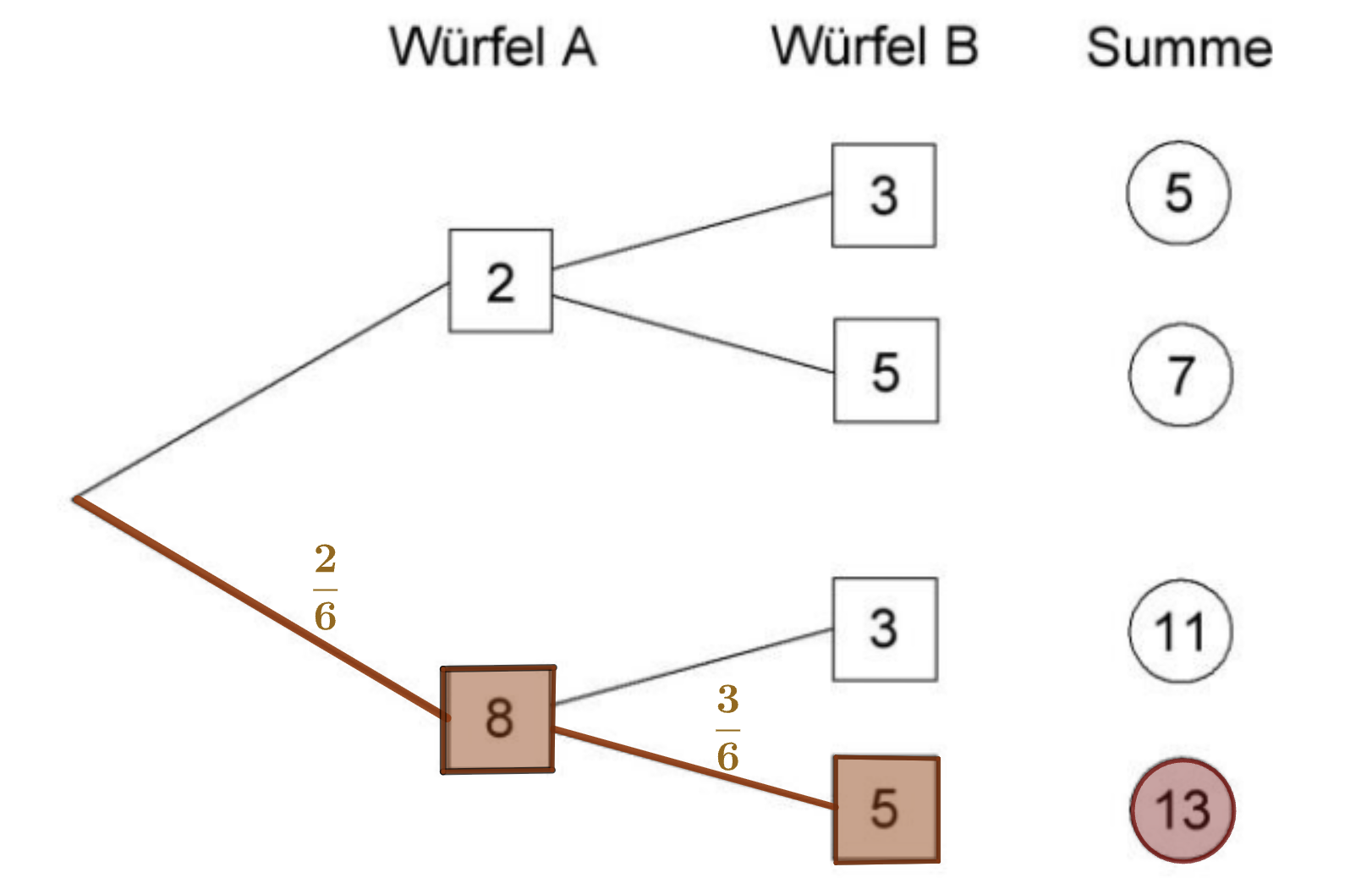
Trage die fehlenden Zahlen in das Baumdiagramm ein und berechne die Summen.
[ 2 Pkte ]
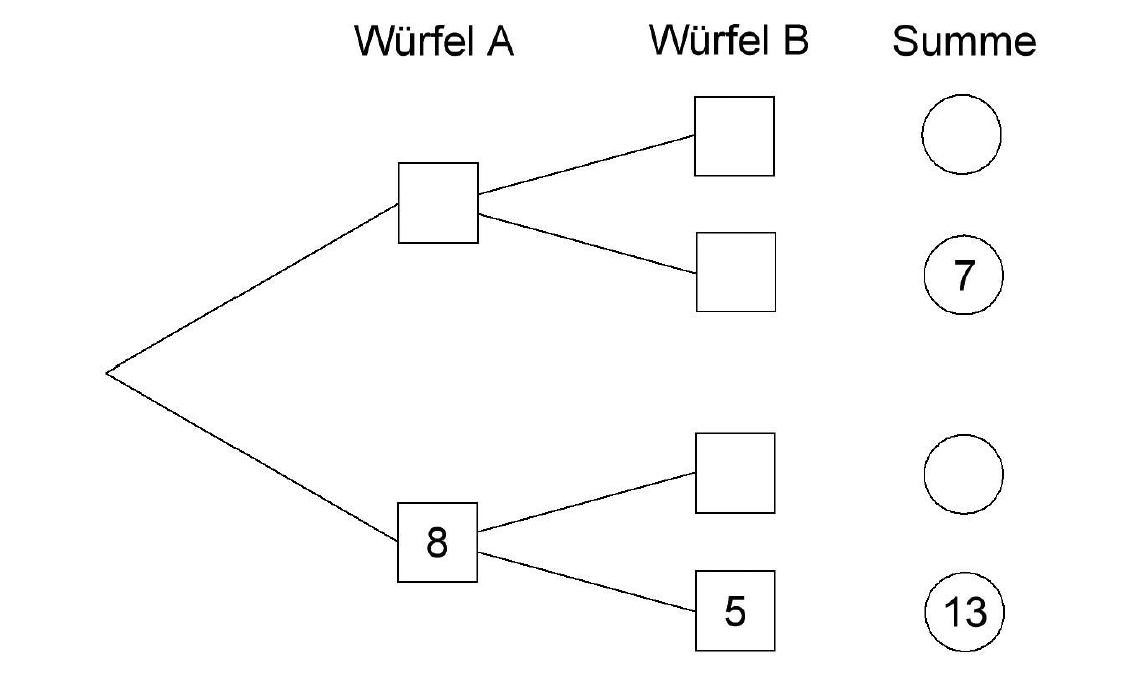
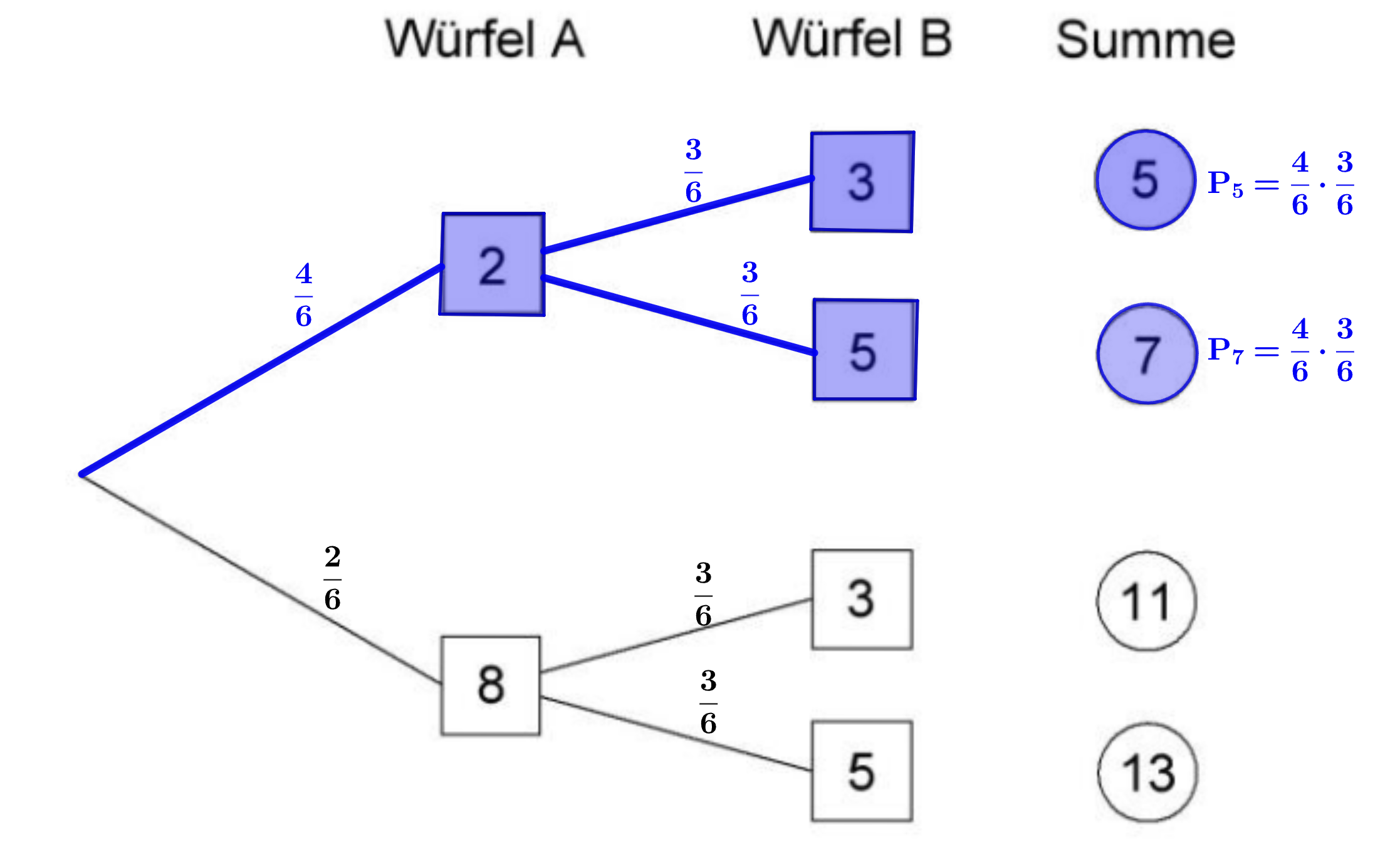
Berechne die Wahrscheinlichkeit, dass die Summe geworfen wird.
[ 2 Pkte ]
Thomas und Moritz vereinbaren ein Spiel mit folgenden Regeln:
− Thomas gewinnt, wenn eine Summe kleiner als geworfen wird.
− Moritz gewinnt, wenn die Summe größer als ist.
− Es gewinnt keiner, wenn die Summe ist.
Berechne die Wahrscheinlichkeit, dass Thomas gewinnt.
[ 2 Pkte ]
Begründe, dass das Spiel nicht fair ist.
[ 1 Pkte ]
Verändere die Spielregel so, dass ein faires Spiel entsteht.
[ 1 Pkte ]
- 4
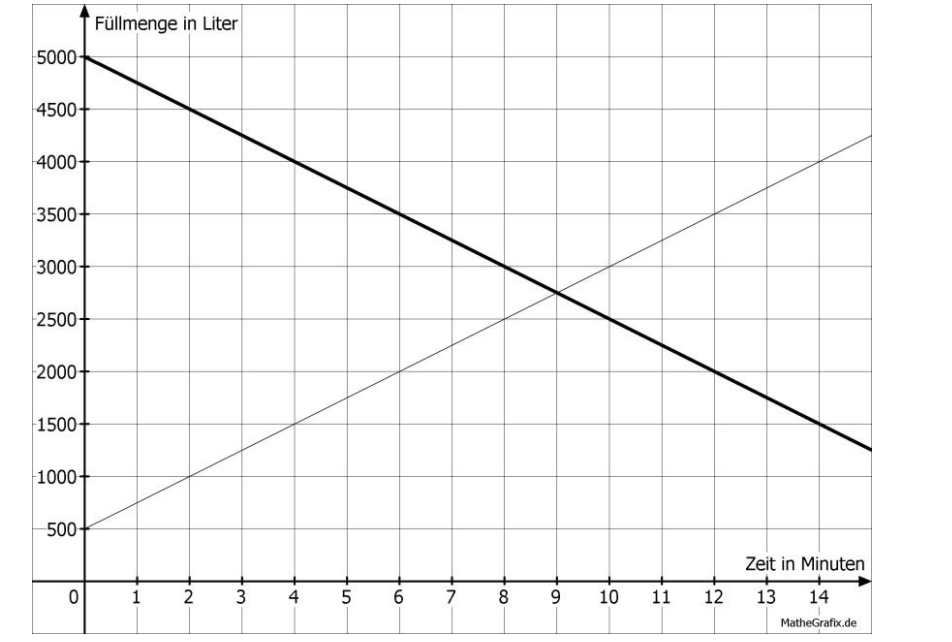
Familie Winter bekommt ihr Heizöl von einem Tankwagen geliefert. Der abgebildete Graph stellt den Füllvorgang des Haustanks dar.
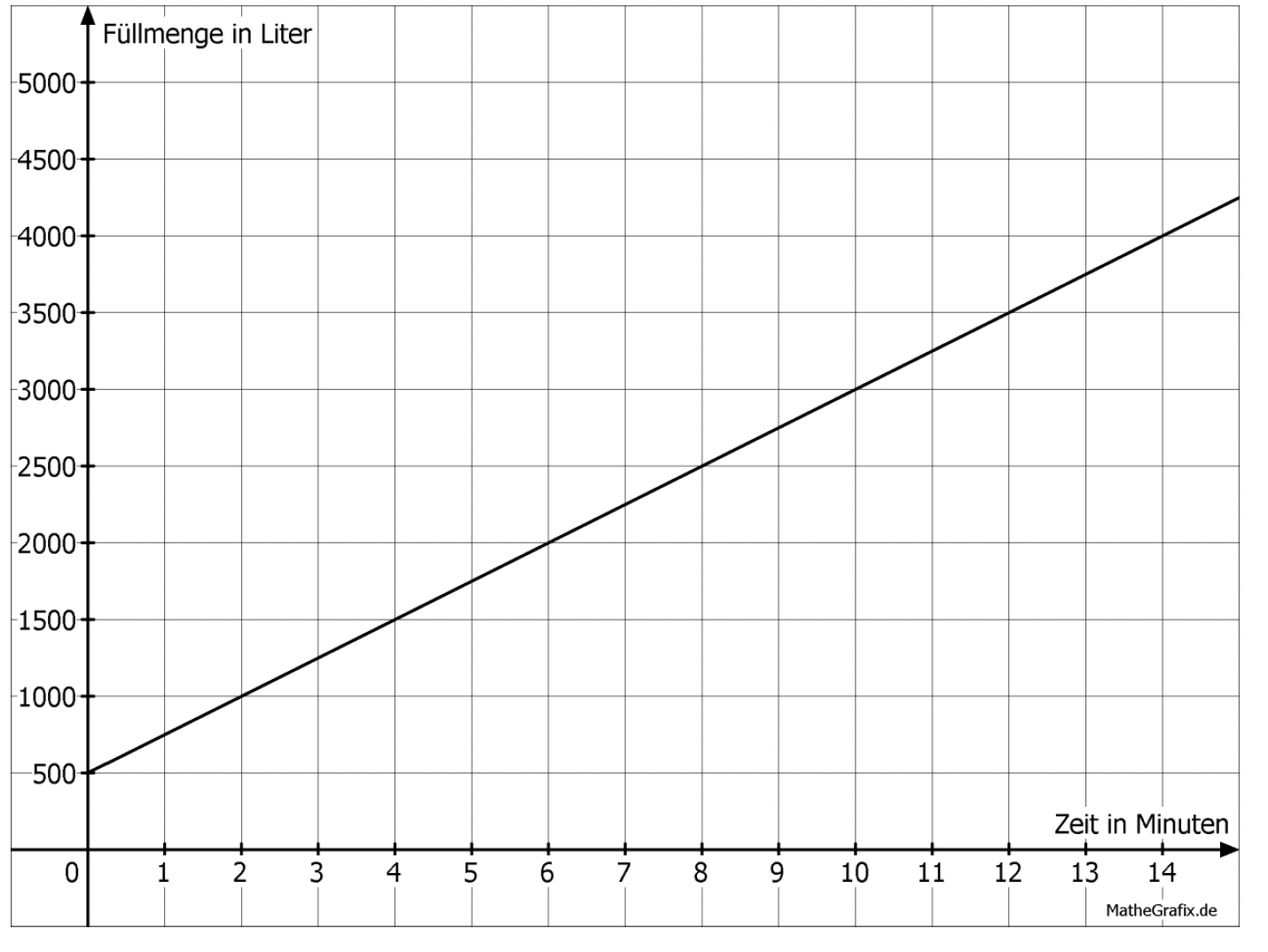
Fülle die Lücken aus.
Zu Beginn des Füllvorgangs befinden sich noch __________ Liter im Haustank.
In den Haustank werden ________ Liter Heizöl pro Minute gepumpt.
[ 2 Pkte ]
Gib die Funktionsgleichung des abgebildeten Graphen in der Form an.
[ 2 Pkte ]
Berechne die Füllmenge, die sich nach Minuten im Haustank befindet.
(Solltest du die Teilaufgabe ) nicht gelöst haben, verwende )
[ 2 Pkte ]
Im Tankwagen befanden sich zu Beginn Liter.
Der Abpumpvorgang des Tankwagens wird durch die Funktionsgleichung
beschrieben.
Zeichne den Graphen für den Abpumpvorgang des Tankwagens in das Koordinatensystem.
[ 2 Pkte ]
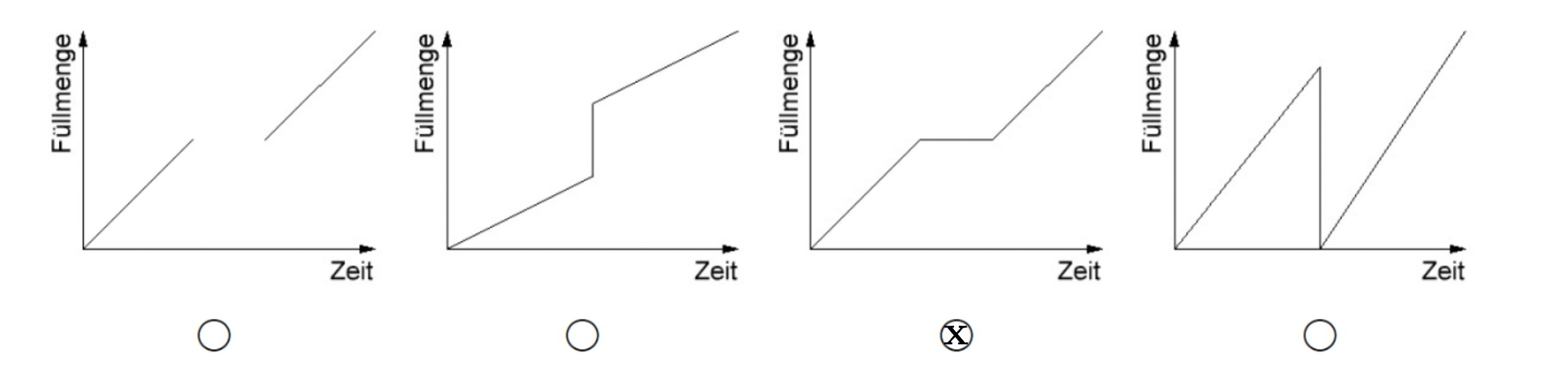
Wenn ein Füllvorgang für einen Zeitraum unterbrochen wird, verändert sich der Verlauf des Graphen.
Kreuze den Graphen an, der einen Füllvorgang mit Unterbrechung darstellt.
[ 1 Pkt ]
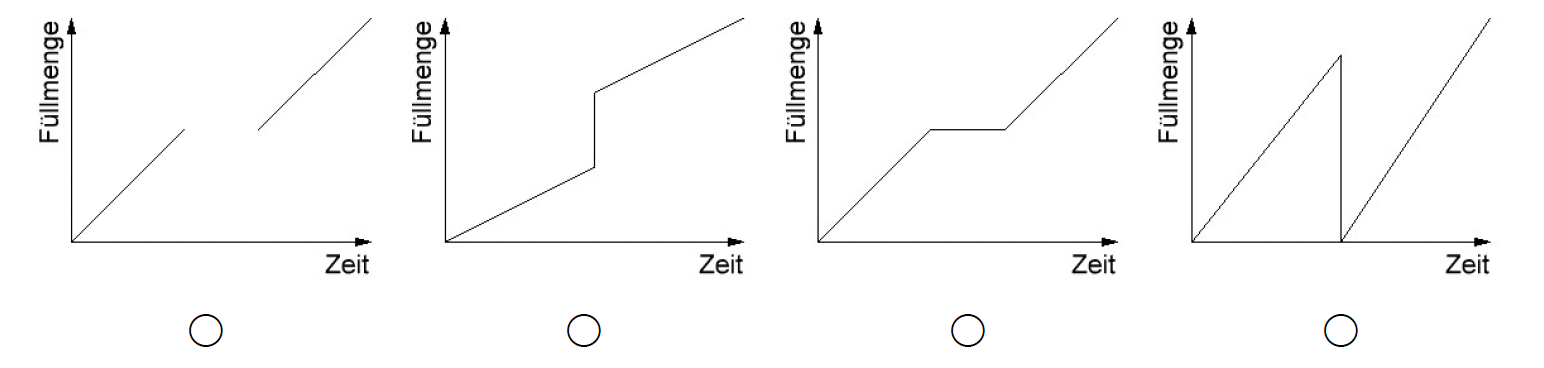
Begründe deine Entscheidung.
[1 Pkt ]
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?