Teil 2
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Die Hauswand soll gestrichen werden.
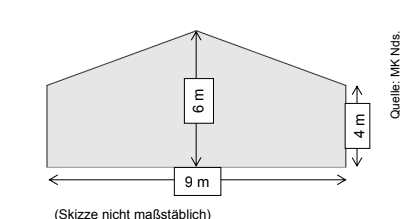
Berechne die Fläche der Hauswand.
[ 4 Pkte ]
Bestimme die Anzahl der benötigten Farb-Eimer.
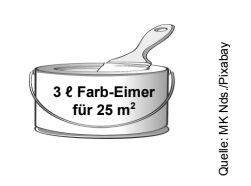
(Wenn du Teilaufgabe a) nicht gelöst hast, dann rechne mit weiter.)
[ 1 Pkt ]
- 2
Rima ist groß. Sie steckt einen Turm aus Bausteinen zusammen, der so groß ist wie sie.
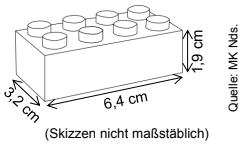
Berechne die benötigte Anzahl an Bausteinen.
[ 1 Pkt ]
Rima baut einen Turm, der so groß ist wie ihr Vater. Sie benötigt dafür Bausteine.
Wie groß ist ihr Vater? Berechne.
[ 1 Pkt ]
Ihr Bruder setzt Bausteine nach folgendem Muster zusammen.
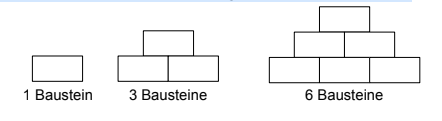
Skizziere das Muster mit Bausteinen.
[ 2 Pkte ]
- 3
Ein Trinkhalm aus Glas steht in einem Pappbecher.
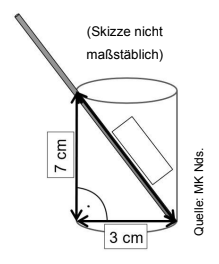
Wie lang ist der Teil des Trinkhalms im Becher? Berechne.
[ 2 Pkte ]
Chris benutzt einen langen Trinkhalm aus Glas. Der leere Pappbecher kippt um, wenn ein Trinkhalm mehr als herausragt. Kippt der Pappbecher mit diesem Trinkhalm um?
Berechne und entscheide.
(Wenn du Teilaufgabe a) nicht gelöst hast, dann rechne mit einer Trinkhalmlänge im Becher von weiter.)
[ 2 Pkte ]
Wie hoch muss der Pappbecher mindestens sein, damit er nicht umkippt? Berechne.
[ 3 Pkte ]
- 4
Die Tabelle zeigt die Nachbarländer von Deutschland mit ihren Einwohnerzahlen.
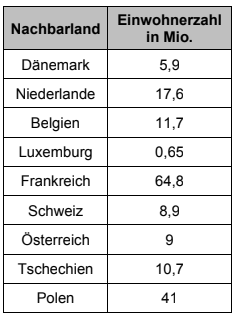
Nenne das Land mit der geringsten Einwohnerzahl. Schreibe die Einwohnerzahl in Ziffern vollständig aus.
[ 2 Pkte ]
Berechne die durchschnittliche Einwohnerzahl der deutschen Nachbarländer.
[ 2 Pkte ]
Deutschland hat ca. 84 300 000 Einwohner
und eine Fläche von 357 588
Berechne die Anzahl der Einwohner pro .
[ 1 Pkt ]
In Berlin leben 3 700 000 Menschen.
Nele behauptet: „In Berlin leben etwa 7 % der Einwohner Deutschlands.“
Hat Nele recht? Kreuze an und begründe.
[2 Pkte ]
- 5
In Hannover gibt es eine Grundgebühr für
Trinkwasser von 20 € pro Jahr.
Jeder Trinkwasser kostet zusätzlich
2 €.
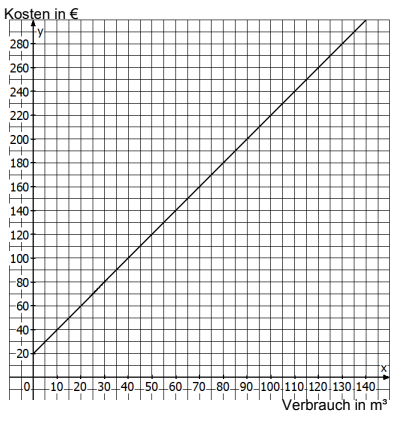
Ergänze die fehlenden Werte in der Tabelle.

[ 3 Pkte ]
Stelle die passende Funktionsgleichung
auf.
y = ________∙ x + _________
[ 2 Pkte ]
Kreuze den passenden Funktionstypen an.
[ 1 Pkt ]
- 6
Das ist ein 12er-Würfel (Dodekaeder).
Die Flächen sind mit den Zahlen 1 bis 12 beschriftet.
Ergänze die Lücken bei einmaligem Würfeln.
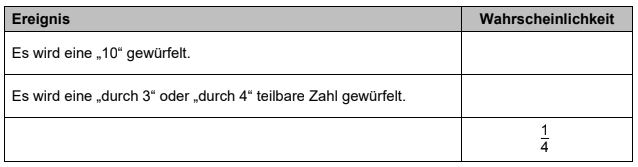
[ 3 Pkte ]
Mohamad und Emrin spielen mit diesem Würfel. Mohamad gewinnt, wenn mindestens eine „9“ gewürfelt wird. Emrin gewinnt, wenn die Zahl höchstens eine „4“ ist. Mohamad beschwert sich: „Das Spiel ist nicht fair.“
Hat Mohamad recht? Kreuze an und begründe.
[ 2 Pkte ]
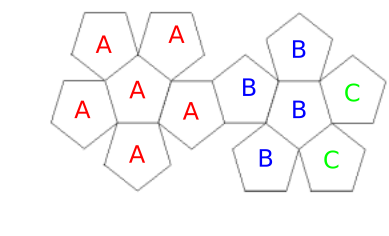
Mohamad zeichnet das Netz eines Dodekaeders.
Beschrifte das Netz mit den Buchstaben A, B und C, sodass folgende Wahrscheinlichkeiten gelten:
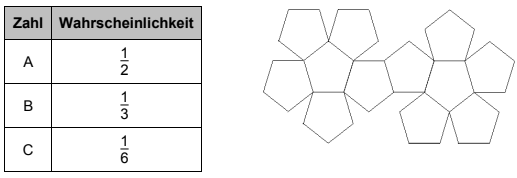
[ 2 Pkte ]
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?