Teil 2 mit Hilfsmitteln Analysis II
- 1
Gegeben ist die Funktion mit der Gleichung und der Definitionsmenge .
Der Graph von wird mit bezeichnet.
Ein Ausschnitt von ist in der nebenstehenden Abbildung zu sehen.
Außerdem ist die Funktion mit der Definitionsmenge gegeben. Weisen Sie nach, dass die Funktion umkehrbar ist.
(7 BE)
Bestimmen Sie eine Gleichung der Geraden , die den Graphen der Umkehrfunktion von in dessen Schnittpunkt mit der x-Achse berührt. (4 BE)
Betrachtet wird die Funktion mit der Definitionsmenge . Ermitteln Sie eine integralfreie Darstellung von .
(6 BE)
Gegeben ist nun die Funktion mit der maximalen Definitionsmenge .
Ermitteln Sie , die Nullstelle von und das Verhalten der Funktionswerte von für . (7 BE)
- 2
Aus einem kompakten, hinreichend langen Zylinder (sog. „zylindrische Welle“) aus Messing sollen für die Schubladen einer Designerkommode rotationssymmetrische Knäufe hergestellt werden (siehe nebenstehende, nicht maßstäbliche Abbildung).
Die Symmetrieachse entspricht dabei der x-Achse in einem kartesischen Koordinatensystem.
Der Graph der Funktion mit der Definitionsmenge beschreibt die obere Konturlinie der Knäufe
(siehe Abbildung).
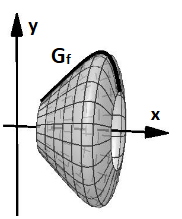
Die x- und y-Koordinaten stellen Längenangaben in der Einheit Zentimeter dar. Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.
Berechnen Sie den Durchmesser , den die zylindrische Welle mindestens haben muss. (5 BE)
Bestimmen Sie die Masse eines Knaufs (auf ganze Gramm gerundet), wenn das verwendete Messing die Dichte besitzt. (6 BE)
- 3
Im Laufe der Wachstumsphase von April bis Anfang Oktober vergrößert sich der Durchmesser eines Baumes.
Dieser Zuwachs kann mithilfe von sogenannten „Dendrometern“ sehr genau gemessen werden. Mit diesen Ergebnissen können Rückschlüsse über Wachstumsbedingungen und klimatische Änderungen gezogen werden.
Die Dendrometer sind vor April installiert worden und haben seit dem 1. April den Zuwachs des Baumdurchmessers gemessen.
Eine Messreihe ist im Diagramm (oben rechts) dargestellt.
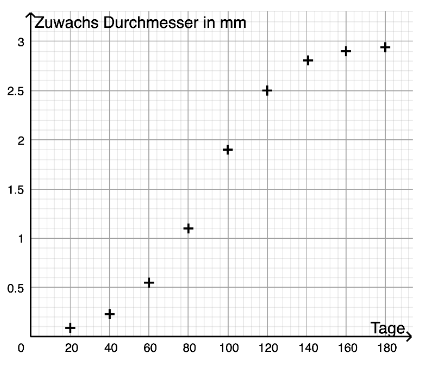
Auf der Abszisse sind die vergangenen Tage ab dem Beobachtungsstart am 1. April angegeben, auf der Ordinate ist der entsprechend gemessene Zuwachs des Durchmessers in vermerkt.
Die Ergebnisse können mithilfe einer mathematischen Funktion mit der Funktionsgleichung mit modelliert werden.
Dabei beschreibt die Zeit in Tagen ab dem 1. April und den Zuwachs des Durchmessers in ab Beobachtungsbeginn .
Weisen Sie nach, dass die Funktion die Differenzialgleichung erfüllt.
(4 BE)
Ermitteln Sie mithilfe der Differenzialgleichung aus a) den maximalen Wert, den annehmen kann, und erläutern Sie dessen Bedeutung im Sachzusammenhang.
(4 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?




