Gemischte Aufgaben zu Zufallsgrößen
Zufall? - Ich glaube nicht. Hier findest du Aufgaben zum Thema Zufallsgrößen und Wahrscheinlichkeit.
- 1
Zwei Würfel, auf deren Seiten 3 Mal die eins und 3 Mal die Zahl zwei vorkommt, werden geworfen. Die Zufallsgröße soll die Augensumme beschreiben und die Zufallsgröße das Produkt der Augenzahlen.
Gib die Wahrscheinlichkeitsverteilungen von und an.
Berechne die Erwartungswerte der beiden Zufallsvariablen.
Berechne Varianz und Standardabweichung der beiden Zufallsvariablen.
- 2
Überraschungseier werben bei einer ihrer Sammelaktionen damit, dass in jedem 7. Ei eine besondere Tierfigur enthalten ist.
Außerdem läuft parallel noch eine andere Aktion,die besagt, dass von den restlichen Eiern die Hälfte Fahrzeuge zum Zusammenbauen enthalten. Du kaufst dir 4 Überraschungseier. Die Zufallsgröße erfasst die Anzahl der Tierfiguren in den 4 Eiern, die Zufallsgröße die Anzahl der Fahrzeuge.
Erläutere, warum es sich bei und um binomialverteilte Zufallsgrößen handelt und gib für die oben beschriebene Situation einen Term zur Berechnung von an.
Stelle die Wahrscheinlichkeitsverteilung der Zufallsgröße T tabellarisch dar.
Bestimme Erwartungswert und Standardabweichung von T.
Bestimme Erwartungswert und Standardabweichung von F.
Silan kauft sich 50 Überraschungseier und beschließt: "Wenn die Anzahl meiner Enthaltenen Tierfiguren kleiner ist als die zweifache Standardabweichung um den Erwartungswert, schreibe ich der Firma. So viel Pech kann ja keiner haben."
Bestimme die Wahrscheinlichkeit für dieses Ereignis und beurteile Silans Entscheidung.
Verena meint "Unabhängig von der Anzahl der gekauften Eier müsste ich immer ungefähr dreimal so viele Fahrzeuge wie Tiere erhalten."
Nehme Stellung zu dieser Aussage.
- 3
In Eulerville wurde über viele Jahre das Wetter untersucht. Es kann abgeschätzt werden, dass es im Monat April dort jeden Tag mit einer Wahrscheinlichkeit von 40% regnet.
Die Zufallsgröße beschreibt die Anzahl der Regentage im April eines Jahres.
Zum Beispiel galt im Jahr 2022 .
Ein Monat wird als statistisch regenarm bezeichnet, wenn die Zufallsgröße einen Wert links von der einfachen Standardabweichung um den Erwartungswert annimmt, als regenstark, wenn er rechts von einer einfachen Standardabweichung um den Erwartungswert liegt und als durchschnittlich, wenn die Anzahl der Regentage sich innerhalb einer einfachen Standardabweichung um den Erwartungswert befindet.
Bestimme Erwartungswert und Standardabweichung der Zufallsgröße .
Erläutere, warum die minimale Anzahl der Tage, die zu einem regenstarken Monat führen, mithilfe von bestimmt werden kann.
Entscheide, ob im Jahr 2022 ein regenstarker April aufgetreten ist.
Bestimme jeweils die Wahrscheinlichkeit dafür, dass ein April als regenarm, durchschnittlich oder regenstark beschrieben wird.
Ist die Anzahl der Regentage höher als der Wert einer doppelten Standardabweichung um den Erwartungswert, so besteht Hochwassergefahr.
Bestimme die Wahrscheinlichkeit eines solchen Ereignisses.
Im Mai ist die Wahrscheinlichkeit für Regen durchschnittlich 28% pro Tag. Bestimme die Schwellenwerte für regenarme, durchschnittliche und regenstarke Mai-Monate sowie die Wahrscheinlichkeit für .
- 4
Bestimme die fehlenden Wahrscheinlichkeiten
-2
0
2
4
a
0,5a
0,24
=a30
40
50
60
a
b
0,2
0,2
Es gilt
- 5
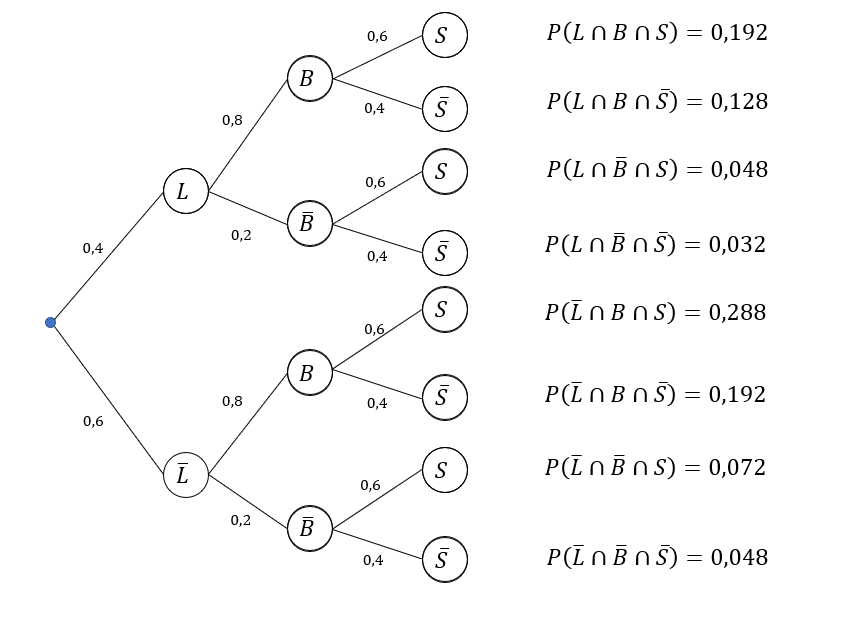
Beim "Fahrrad-TÜV" eines ehrenamtlichen Vereins wird untersucht, ob Licht (L), Bremsen (B) und Schaltung (S) funktionieren. Aus Erfahrung ist bekannt, dass bei 60% der Fahrräder das Licht defekt ist. Unabhängig von Licht und Schaltung sind bei 20% der Fahrräder die Bremsen nicht in Ordnung. Ebenfalls unabhängig von den beiden anderen Mängeln funktioniert die Schaltung bei 40% der Fahrräder nicht mehr einwandfrei.
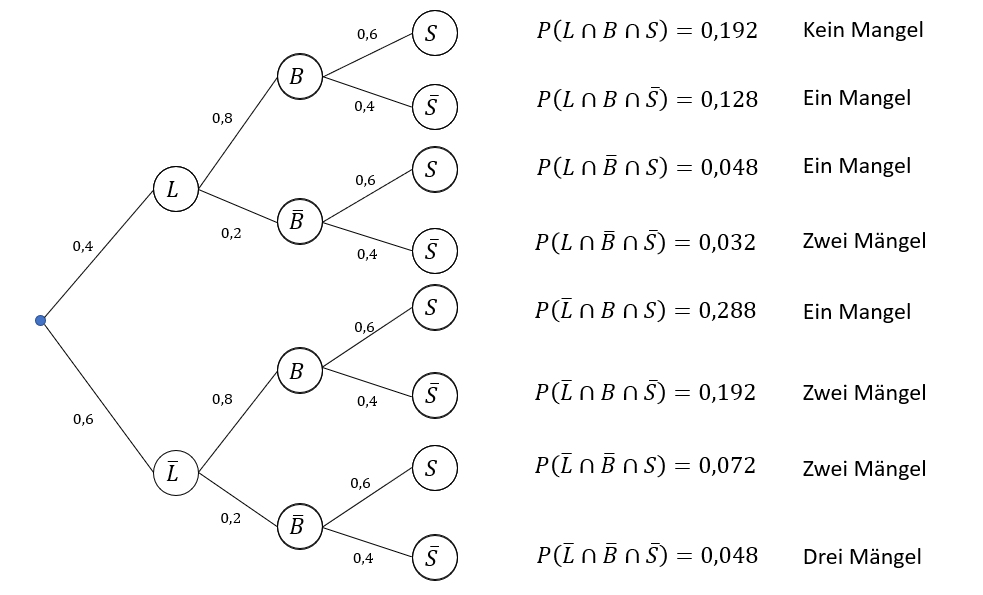
Die Zufallsgröße M beschreibt die Anzahl der Mängel, die ein Fahrrad aufweisen kann.
Bestimme mithilfe eines Baumdiagramms die relativen Häufigkeiten aller möglichen Fahrradzustände.
Bestimme, wie viele Mängel ein Fahrrad durchschnittlich hat.
Der Verein bietet auch Fahrradreparaturen an. Durchschnittlich nimmt er pro Fahrrad 80€ ein, wobei die Reparatur von Licht 30€ und die Reparatur der Schaltung doppelt so viel wie die Reparatur der Bremsen kostet. Theo bringt einen Totalschaden zur Werkstatt. Ermittle, wie viel die Reparatur der drei Mängel kostet.
- 6
"Wenn am nächsten Sonntag Landtagswahlen wären, wen würden Sie wählen?"
Auf diese Frage antworteten in Bayern (am 12.01.23) 40% der Befragten, dass Sie die CSU wählen würden. 20% wollen die Grünen wählen.
Du befragst selbst 200 Personen auf der Straße. Die Zufallsgröße C gibt an, wie viele Personen die CSU präferieren, die Zufallsgröße G beschreibt die Anzahl der Personen, die die Grünen wählen würden.
(Andere Parteien wurden Aufgrund der Übersichtlichkeit weggelassen, es handelt sich um die beiden meistgenannten Parteien)
Bestimme die Erwartungswerte der beiden Zufallsgröße und erläutere ihre Bedeutung im Sachkontext.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?