Aufgaben zum Thema Analysis

1
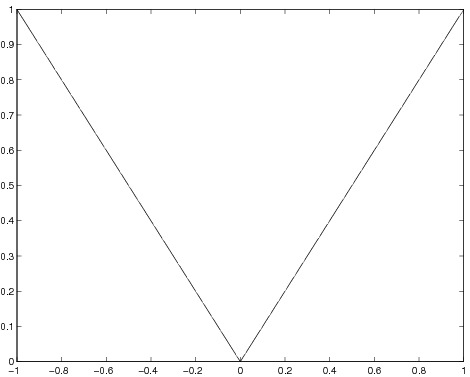
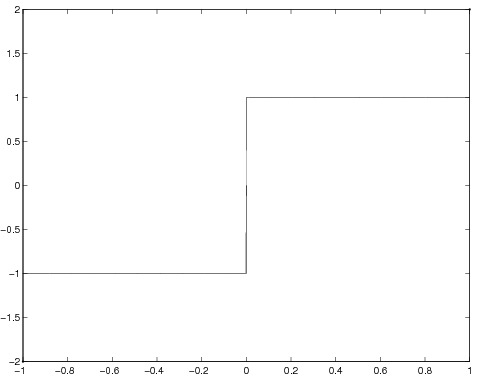
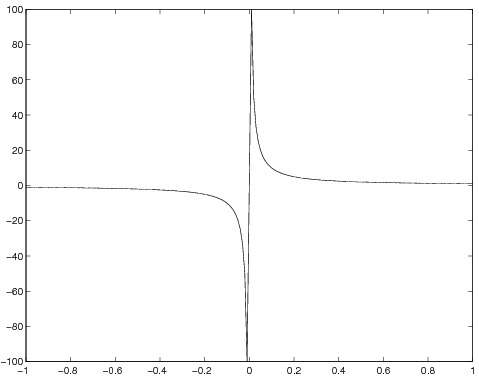
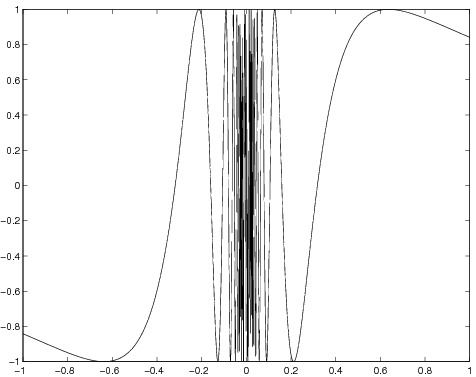
Entscheide, ob die folgenden Funktionen stetig sind (ohne Begründung).
2. $f(x) = \text{sign}(x) = \begin{cases} 1, & \text{für}\ \ x>0, \\ 0, & \text{für}\ \ x = 0, \\ -1, & \text{für} \ \ x < 0. \end{cases}$
6. $f(x) = \begin{cases} 1, & \text{für}\ \ x \in \mathbb{Q}, \\ -1, & \text{für}\ \ x \notin \mathbb{Q}. \end{cases}$
2
Zeige direkt anhand der $\epsilon$ - $\delta$ -Definition die Stetigkeit der Funktion $f(x) = |x|$ . Wie kannst du anhand der $\epsilon$ - $\delta$ -Definition zeigen, dass die Signumsfunktion
$\mathrm{sign}(x) =\begin{cases}1 & \text{ f} \mathrm{\ddot{u}} \text{r } x > 0 \; , \\0 & \text{ f} \mathrm{\ddot{u}} \text{r } x = 0\; , \\-1 & \text{ f} \mathrm{\ddot{u}} \text{r } x < 0\;\end{cases}$ in $x=0$ nicht stetig ist?
3
Leite mit Hilfe der Kettenregel die Ableitung von $\frac{1}{g(x)}$ und anschließend mit der Produktregel die Ableitung von $\frac{f(x)}{g(x)}$ her.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Analysis
Zur Erinnerung: Die Kettenregel lautet: $(h(g(x)))'=h'(g(x))g'(x)$ .
Wenn wir nun $\displaystyle \frac{1}{g(x)}$ ableiten wollen, dann können wir
wählen und die Kettenregel benutzen:
$\displaystyle (h(g(x)))'=h'(g(x))g'(x)=-\frac{1}{(g(x))^2}g'(x)=-\frac{g'(x)}{(g(x))^2}\quad\quad\blacksquare$
Nun kommen wir zum zweiten Teil der Aufgabe, dem Ableiten von
Dazu wenden wir die Produktregel und die gerade ermittelte Ableitungsregel an:
Und damit sind wir bei der Quotientenregel gelandet.
4
Der Mittelwertsatz der Differentialrechnung lautet:
Die Funktion $f$ sei im Intervall $[a,b]$ mit $a<b$ stetig und im Inneren $(a,b)$ differenzierbar.
Dann existiert ein $c\in[a,b]$ mit
$f(b)-f(a)=f'(c)(b-a).$
1. Was bedeutet dieser Satz anschaulich?
2. Beweise den Satz von Rolle:
  Die Funktion $f$ sei im Intervall $[a,b]$ stetig differenzierbar und es gelte $f(a)=f(b)$ .Dann besitzt der Graph von $f$ zwischen $a$ und $b$ mindestens einen Punkt mit waagrechter Tangente.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Analysis
  An einem Punkt $x$ , an dem $f$ eine waagrechte Tangente hat, gilt $f'(x)=0$ (da die waagrechte Tangente nicht steigt oder fällt).Wenn $f(a)=f(b)$ , dann ist natürlich $f(b)-f(a)=0$ .Nun betrachten wir den Mittelwertsatz (wir haben ja vorausgesetzt, dass $f$ im Intervall $[a,b]$ stetig differenzierbar ist; zusätzlich muss $a \neq b$ gelten, denn sonst wäre, sobald der Satz bewiesen ist, in jedem Punkt eine waagrechte Tangente):
  Mit der oben erkannten Eigenschaft ergibt sich:
  Da wir $a\neq b$ noch zusätzlich vorausgesetzt haben, können wir durch $(b-a)$ dividieren:
  Und damit haben wir am Punkt $\xi\in[a,b]$ eine waagrechte Tangente. Da nach mindestens einer solcher verlangt war, haben wir den Satz von Rolle bewiesen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Aufgaben zum Thema Analysis

Hast du eine Frage oder Feedback?