10. Analysis

Stetigkeit von Funktionen

EineFunktion $f (x)$ : $ℝ \to ℝ$ ist stetig bei $a \in ℝ$ , wenn gilt, dass der linksseitige und der rechtsseitige Grenzwert gleich dem Funktionswert sind:

\lim_{h \to 0^{+}} f (a + h) = f (a) = \lim_{h \to 0^{-}} f (a + h)

Andere Definition: Zu gegebenem $ϵ > 0$ gibt es ein $δ > 0$ , so dass gilt:

| a - ζ | < δ \Rightarrow | f (a) - f (ζ) | < ϵ

Anschaulich: Die Funktion macht keine Sprünge!

Differentialrechnung

Ableitung von $f (x)$ an der Stelle $a$ :

\lim_{h \to 0} \frac{f (a + h) - f (a)}{h} = \lim_{△ x \to 0} \frac{△ y}{△ x}

Ableitung an allen Stellen $a$ ergibt wieder eine neue Funktion $f^{'} (a)$

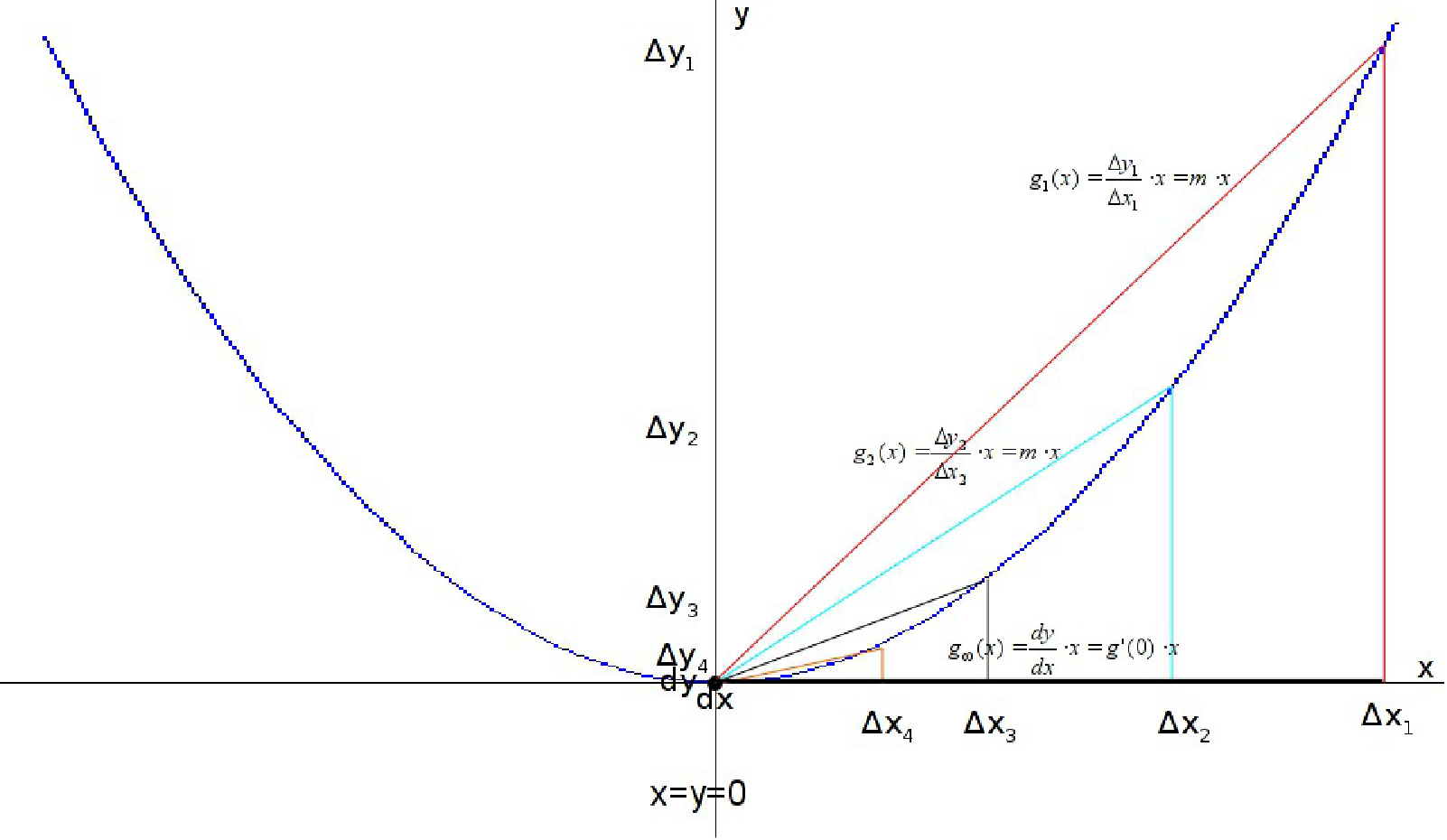
Beispiel: Ableitung von $f (x) = x^{n}$ :

\begin{aligned} \lim_{h \to 0} \frac{(a + h)^{n} - a^{n}}{h} & = \lim_{h \to 0} \frac{(a^{n} + n h a^{n - 1} + \dots + h^{n}) - a^{n}}{h} \\ = \lim_{h \to 0} \frac{n h a^{n - 1} + \dots + h^{n}}{h} \\ = n a^{n - 1} \Rightarrow \frac{d}{d x} x^{n} = n x^{n - 1} \end{aligned}

Herleitung der Exponentialfunktion. Gegeben $f (x) = \sum_{k = 0}^{\infty} a_{k} x^{k}$ mit beliebigen $a_{k}, k \geq 0$ .

Gesucht sind die Koeffizienten $a_{k}$ , so dass $f^{'} (x) = f (x)$ :

f^{'} (x) = \sum_{k = 1}^{\infty} a_{k} k x^{k - 1} = \sum_{k = 0}^{\infty} a_{k + 1} (k + 1) x^{k} \overset{!}{=} \sum_{k = 0}^{\infty} a_{k} x^{k} = f (x)

Koeffizientenvergleich ergibt:

a_{k + 1} = \frac{a_{k}}{k + 1} = \frac{a_{k - 1}}{(k + 1) k} = \frac{a_{k - 2}}{(k + 1) k (k - 1)} = \dots = \frac{a_{0}}{(k + 1)!}

mit der Lösung

f (x) = a_{0} \sum_{k = 0}^{\infty} \frac{1}{k!} x^{k} = a_{0} \exp (x) .

Weitere Ableitungen:
$\frac{d}{d x} x^{n} = n x^{n - 1}$
$\frac{d}{d x} e^{x} = e^{x}$
$\frac{d}{d x} \ln (x) = \frac{1}{x}$
$\frac{d}{d x} \sin (x) = \cos (x)$
$\frac{d}{d x} \cos (x) = - \sin (x)$

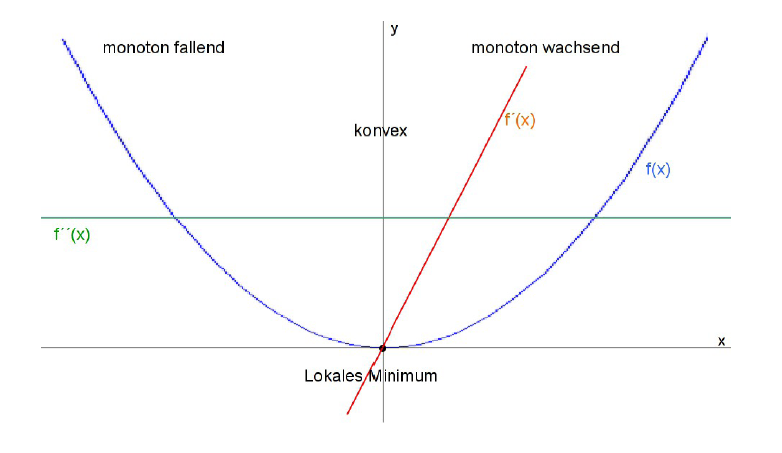
Monotonie: Ist die Ableitung an einer Stelle $a$ größer $0$ , so weist die Tangente nach oben und die Funktion selbst ist bei $a$ monoton wachsend.
Ist die Ableitung an einer Stelle $a$ gleich $0$ , so hat die Funktion bei $a$ eine waagrechte Tangente:
lokales Maximum oder Minimum
Sattelpunkt
Ist die zweite Ableitung an einer Stelle $a$ größer $0$ , so weist die Tangente der Ableitung nach oben und die Ableitung selbst ist monoton wachsend.Die Funktion selbst ist dann bei $a$ konvex gekrümmt:

Ableitungsregeln
Produktregel: $\frac{d}{d x} g (x) f (x) = g (x) f^{'} (x) + g^{'} (x) f (x)$

Kettenregel (gilt $y = g (x)$ und $z = f (y)$ , so gilt auch $z = f (g (x))$ ): $\frac{d}{d x} f (g (x)) = f^{'} (g (x)) g^{'} (x)$

Kurvendiskussion der Funktion
$f (x) = \frac{x - 1}{x^{2}} = \frac{1}{x} - \frac{1}{x^{2}}$
mit den Ableitungen
$f^{'} (x) = - \frac{1}{x^{2}} + \frac{2}{x^{3}} = \frac{2 - x}{x^{3}}, f^{''} (x) = \frac{2}{x^{3}} - \frac{6}{x^{4}} = \frac{2 x - 6}{x^{4}}$
Nullstellen von $f (x)$ sind $x_{0} = 1$ . Somit gilt für $x > 1 \to f (x) > 0$ und
$x < 1 \to f (x) < 0$
Polstellen von $f (x)$ sind $x_{1} = 0$ . Für $x > 2 \to f^{'} (x) < 0$ ist $f (x)$ monotonfallend. Für $0 < x < 2 \to f^{'} (x) > 0$ ist $f (x)$ monoton wachsend. Für $x < 0 \to f^{'} (x) < 0$ ist $f (x)$ monoton fallend.
Nullstelle von $f^{'} (x)$ : $x_{2} = 2$ wobei $f (2) = \frac{1}{4}$ .
Für $x > 3$ ist $f^{''} (x) > 0$ und damit $f (x)$ konvex.
Für $x < 3$ ist $f^{''} (x) < 0$ und damit $f (x)$ konkav.
Grenzwertbetrachtung:
$\lim_{x \to \pm \infty} f (x) = \lim_{x \to \pm \infty} (\frac{1}{x} - \frac{1}{x^{2}}) = 0.$

Aufgaben

Laden

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?