1 Übersicht
Inhalt des Kurses
In diesem Kurs lernst du, wie du die Länge eines Vektors oder den Winkel zwischen zwei Vektoren berechnest. Es werden unter anderem Begriffe wie das Skalarprodukt eingeführt. Des Weiteren wird die Flächenberechnung eines Dreiecks mithilfe von Determinanten behandelt.
Vorkenntnisse
Du solltest die Definition eines Vektors verstanden haben. Zur Wiederholung kann man sich den Kurs Einführung in den Vektorbegriff (Vektoren in der Ebene I) anschauen.
Du solltest mit Vektoren rechnen können. Dies wird im Kurs Rechnung mit Vektoren (Vektoren in der Ebene II) behandelt.
Du kannst den Kurs besser verstehen, wenn du den Satz des Pythagoras bereits kennst.
Kursdauer
ca. 3 Stunden
2 Länge eines Vektors
Ein Vektor und seine Repräsentanten sind eindeutig durch ihre Richtung und Länge festgelegt (dies wird im Kurs Vektoren in der Ebene I behandelt).
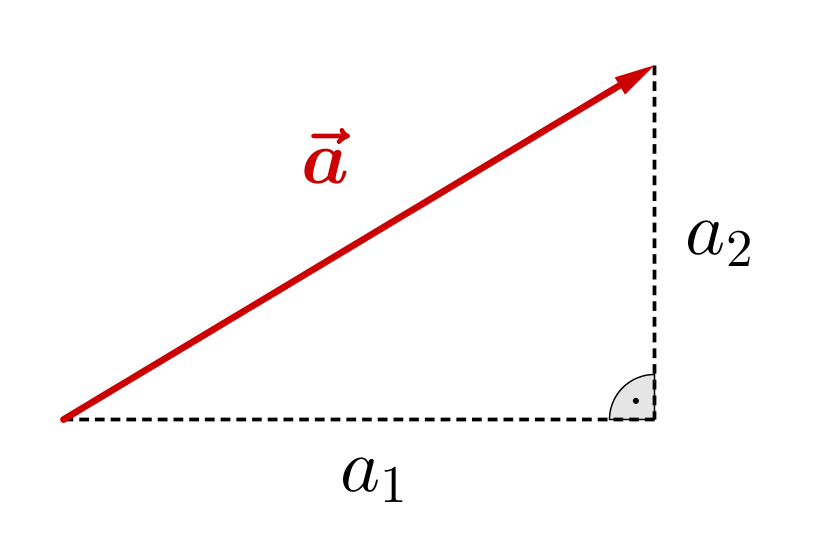
Die Länge eines Vektors oder der Betrag eines Vektors ist der Abstand von seiner Spitze zu seinem Fuß.
Schreibweise:
Die Länge des Vektors ist gegeben durch:
Das kann man mithilfe des Satzes des Pythagoras zeigen:
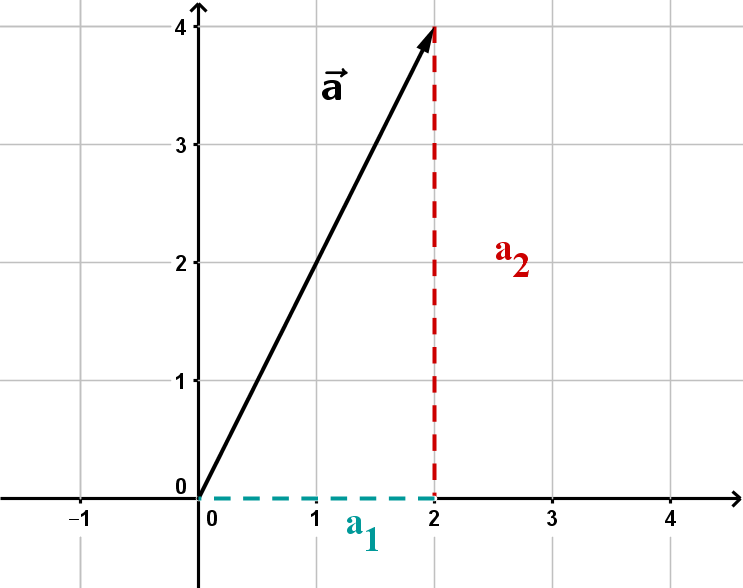
3 Beispiel: Länge eines Vektors
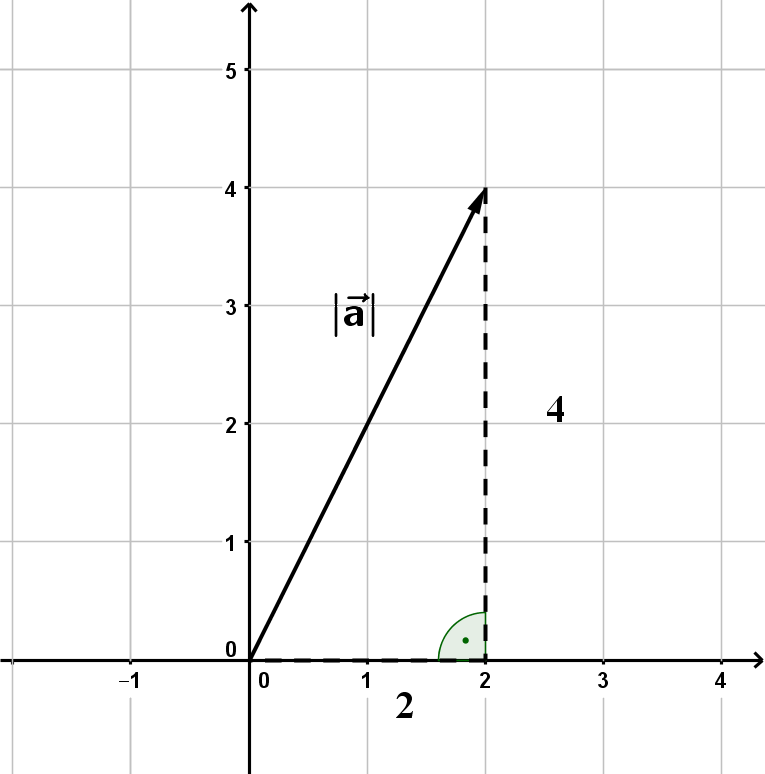
Falls man den Abstand zweier Punkte ( und ) berechnen möchte, stellt man zuerst den Vektor auf und berechnet dann dessen Länge.
4 Aufgaben: Länge eines Vektors
Laden
5 Skalarprodukt
Das Skalarprodukt ist eine Art "Multiplikation" von Vektoren, deren Ergebnis eine reelle Zahl ist. Man schreibt.
Man bestimmt es folgendermaßen: Gegeben sind zwei Vektoren und
Dann ist
Orthogonalität
Ein Vektor ist orthogonal zu einem Vektor , wenn die beiden Vektoren senkrecht zueinander stehen. Dies kann man durch das Skalarprodukt beider Vektoren überprüfen.
Ist dieses nämlich gleich null, so sind und orthogonal zueinander. D.h.:
(wenn, und )
Vektoren müssen nicht immer orthogonal zueinander sein.
Diese Vektoren erkennt man daran, dass deren Skalarprodukt ungleich null ist, d.h. deren Repräsentanten stehen nicht zueinander im rechten Winkel.

Es gilt:
nicht senkrecht zu
Beachte: Es ist unwichtig, ob die Vektoren einen gemeinsamen Fußpunkt haben, denn man kann einfach ihre Repräsentanten nehmen, die im Ursprung ihre Fußpunkte haben (Ortsvektoren).
Am Ergebnis des Skalarprodukts, geschweige denn am Vektor selber, ändert sich selbstverständlich nichts.
6 Beispiele: Skalarprodukt
1.
Es sind die Vektoren
und
gegeben. Man soll das Skalarprodukt bestimmen und daraus schließen, ob die beiden Vektoren zueinander orthogonal sind.
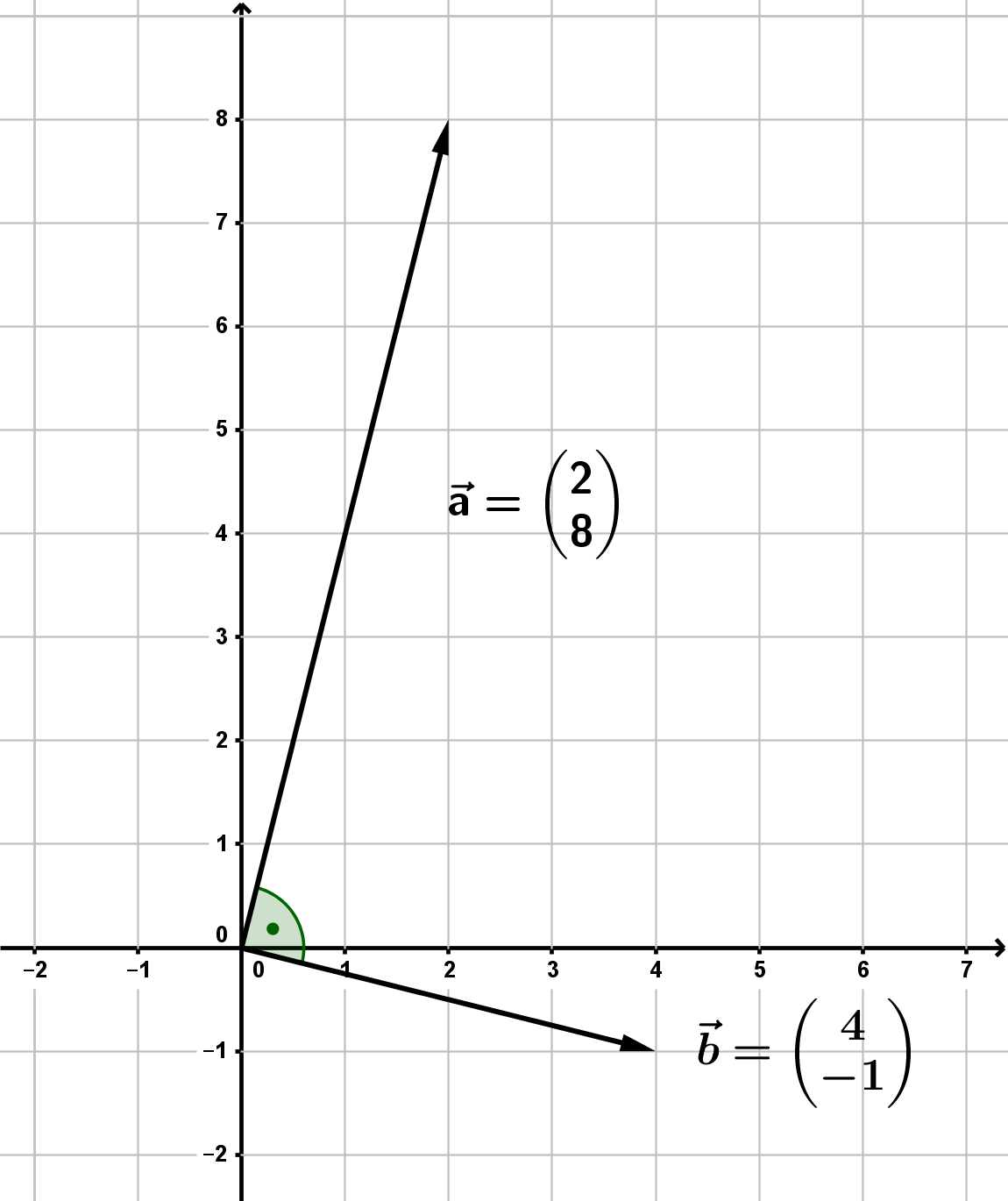
2.
Man hat die Punkte
und
gegeben. Nun soll überprüft werden, ob die Vektoren und orthogonal zueinander sind.
Zunächst werden die Vektoren und berechnet. Das Skalarprodukt wird ganz normal berechnet.
Das Skalarprodukt berechnet sich dann wie in Beispiel 1. oben durch
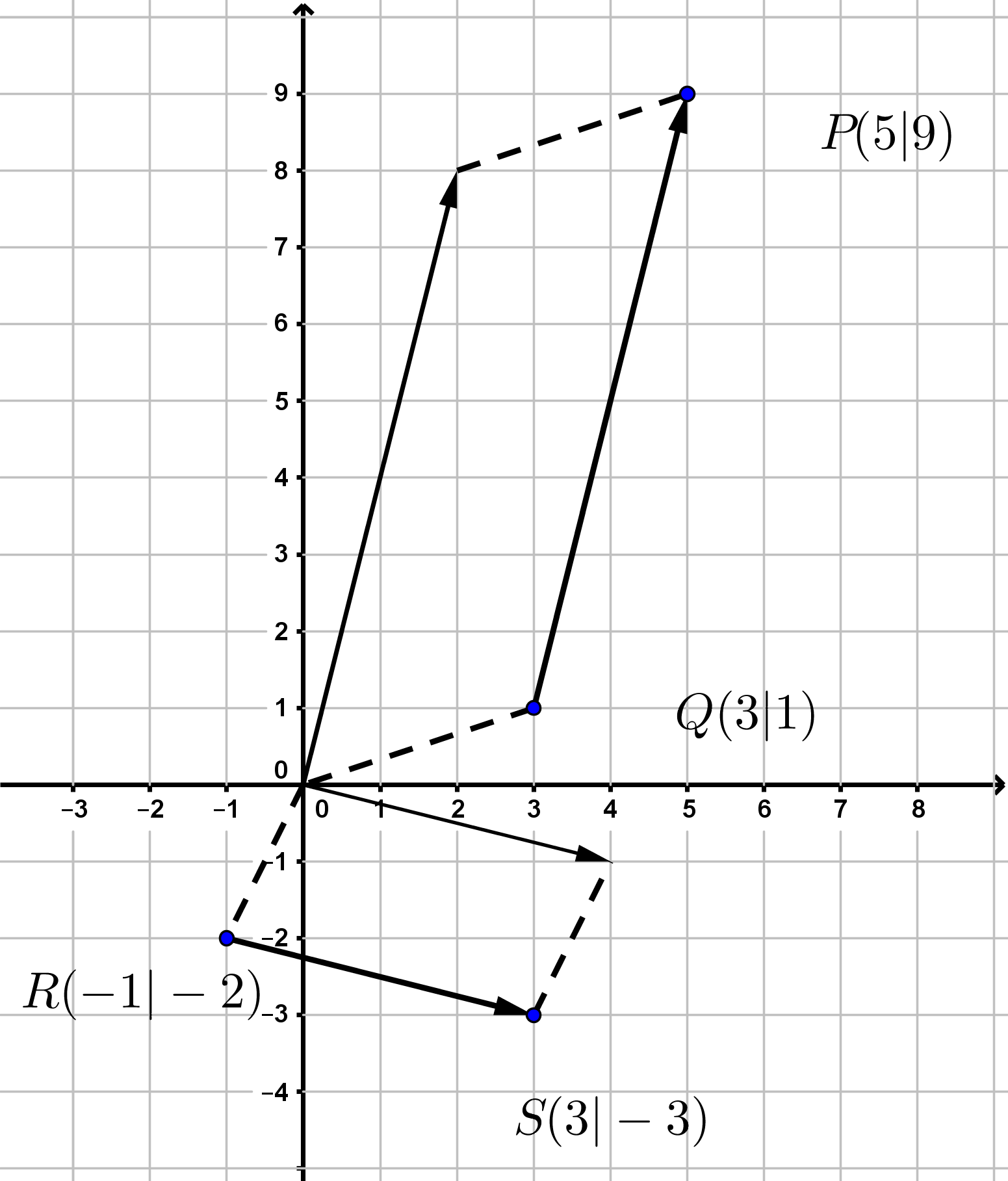
3.
Es sind die Vektoren
und
gegeben. Man soll das Skalarprodukt bestimmen und daraus schließen, ob die beiden Vektoren zueinander orthogonal sind.
Demnach sind die beiden Vektoren nicht orthogonal zueinander.

7 Aufgaben zum Skalarprodukt
Laden
8 Winkel
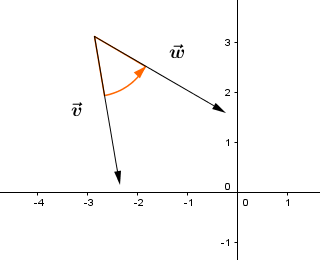
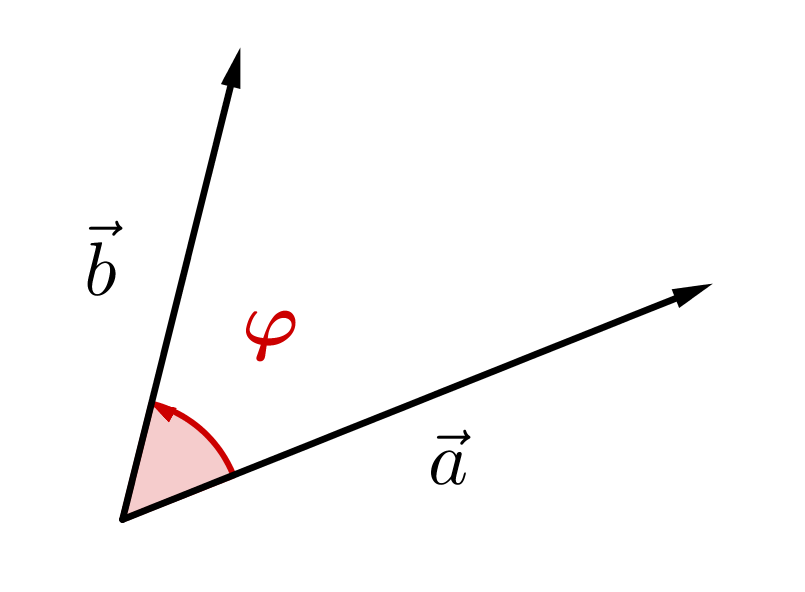
Man kann jetzt den Winkel zwischen zwei Vektoren bestimmen. Das geschieht immer gegen den Uhrzeigersinn.*
Rechts im Bild kannst du sehen, dass es dafür zwei Möglichkeiten gibt: Den kleineren Winkel und den größeren Winkel . Man gibt aber normalerweise immer nur den kleineren an.
Es gilt immer: .
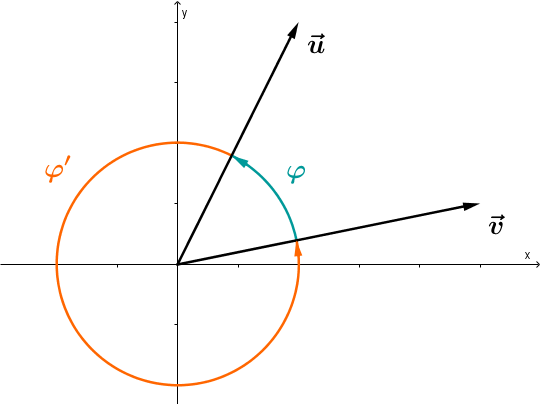
Die Berechnung des Winkels zwischen und geht folgendermaßen:
beziehungsweise
Der größere Winkel lässt sich dann so berechnen:
Dabei steht das "" für das Skalarprodukt.
"" ist die inverse Kosinus-Funktion: der Arkuskosinus. Das bedeutet insbesondere, dass
9 Beispiel: Winkel
Beispiel
Gegeben seien die beiden Vektoren und . Man soll nun den Winkel zwischen und ausrechnen.
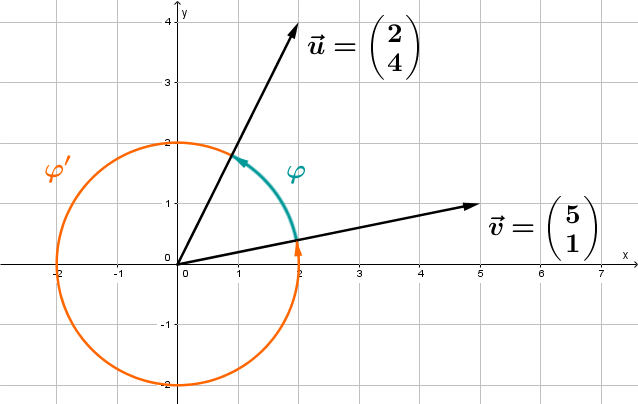
Dazu benutzt man die soeben gelernte Formel:
Einsetzen:
Daraus folgt:
Der gesuchte Winkel beträgt also . Falls auch der größere Winkel gefragt ist, kann man ihn jetzt ganz einfach angeben:
10 Aufgaben zum Winkel
Laden
11 Determinante
Nun kann man mithilfe von Vektoren die Fläche von geometrischen Figuren bestimmen. Hierfür benutzt man die Determinante. Diese ordnet einer quadratischen Matrix eine reelle Zahl zu.
Man schreibt: oder .
Es gilt:
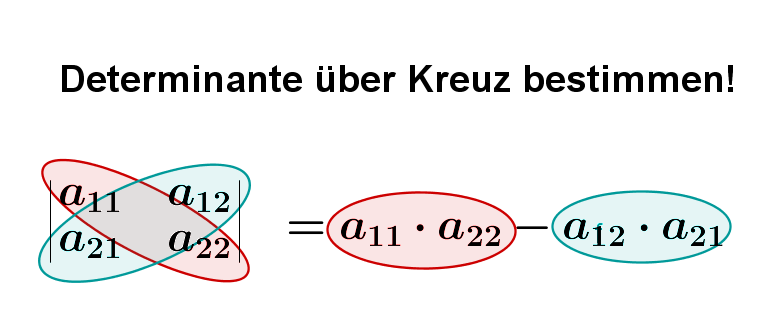
Meistens hat man zwei Vektoren und gegeben, die man in die Determinate einsetzt:
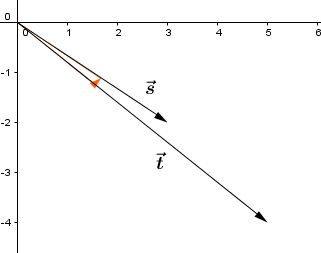
Die Reihenfolge, welchen Vektor man zuerst einsetzt, ist nicht beliebig. Sie erfolgt entgegen dem Uhrzeigersinn!
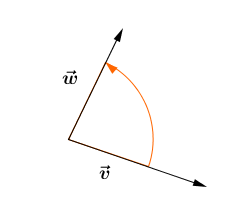
Beispiel
Gegeben sind und . Du sollst nun die Determinante bestimmen.
Dann ist:
12 Aufgaben zur Determinante
Laden
13 Flächenberechnung
Vektoren können auch hilfreich sein, um den Flächeninhalt von Dreiecken und anderen Figuren auszurechnen.
Flächenberechnung an einem Dreieck
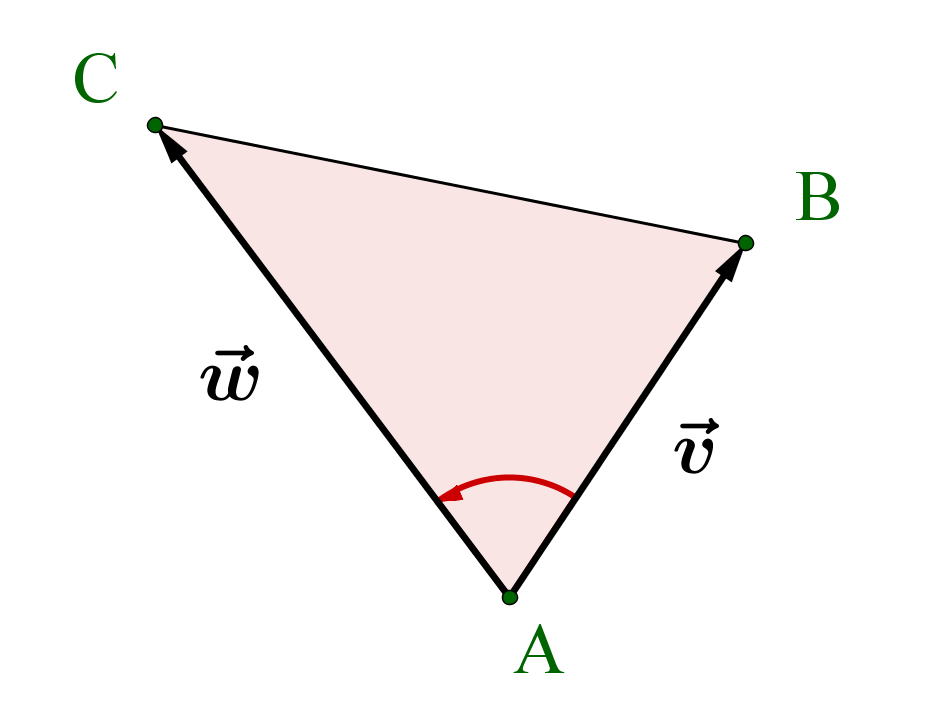
Bei drei gegebenen Punkten , und eines Dreiecks bestimmst du zuerst zwei Verbindungsvektoren und .
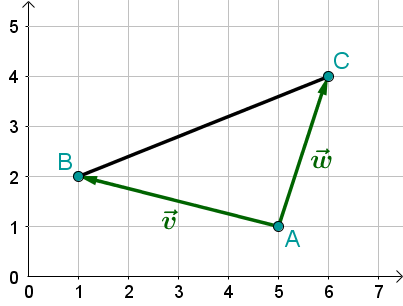
Jetzt kann der Flächeninhalt des Dreiecks mit folgender Formel berechnet werden:
Dabei ist die Determinante von und . Die Reihenfolge der beiden Vektoren ist vorgegeben: entgegen dem Uhrzeigersinn.
Falls man die Vektoren in der falschen Reihenfolge einträgt, erhält man ein negatives Ergebnis.
14 Beispiel: Flächenberechnung
Gegeben:
Ein Dreieck mit den Punkten , und .
Gesucht:
Der Flächeninhalt des Dreiecks.
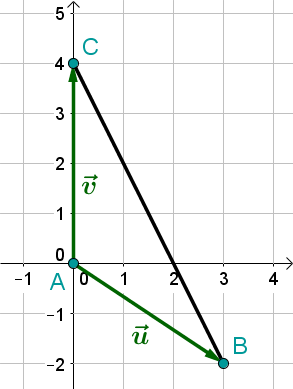
Zuerst berechnet man und .
Mit der Formel folgt:
15 Beispiel: Flächenberechnung in Abhängigkeit von x
Die Eckpunkte eines Dreiecks müssen nicht immer fest vorgegeben sein. Es kann auch einen Punkt geben, der sich auf einer Funktion bewegt, also von einer Variablen abhängt.
In diesem Fall kann man allgemein den Flächeninhalt in Abhängigkeit von berechnen.
Gegeben:
Ein Dreieck mit , und .
Gesucht:
Der Flächeninhalt des Dreiecks .
Zuerst berechnest du und .
Mit der Formel folgt:
16 Applet: Flächenberechnung in Abhängigkeit von x
17 Aufgaben zur Flächenberechnung
Laden
Laden
Laden
Laden
Laden
18 Zusammenfassung
Neben der Addition, Subtraktion und Skalarmultiplikation können noch weitere Operationen mit Vektoren durchgeführt werden:
Betrag eines Vektors
Der Betrag eines Vektors gibt seine Länge, also den Abstand von Spitze und Fuß, an:
Skalarprodukt
Man kann zwei Vektoren miteinander "multiplizieren", indem man das Skalarprodukt bildet; als Ergebnis liefert es eine Zahl (="Skalar").
Orthogonalität: (wenn und )
Mithilfe des Skalarprodukts kann außerdem allgemein der (kleinere der beiden) Winkel zwischen zwei Vektoren bestimmt werden:
Flächenberechnung mittels Determinante
Mithilfe der Determinante, die zwei Vektoren ebenfalls eine reelle Zahl zuordnet, lässt sich beispielsweise der Flächeninhalt eines Dreiecks bestimmen.
Dabei wird die Reihenfolge der Vektoren gegen den Uhrzeigersinn gebildet:
19 Zeige, was du kannst!
Laden
