Gemischte Aufgaben

Teste dein Wissen zum Rechnen mit Vektoren! Übe Addition, Subtraktion, skalare Multiplikation und Vektorketten und lerne, das Ergebnis grafisch darzustellen.

1
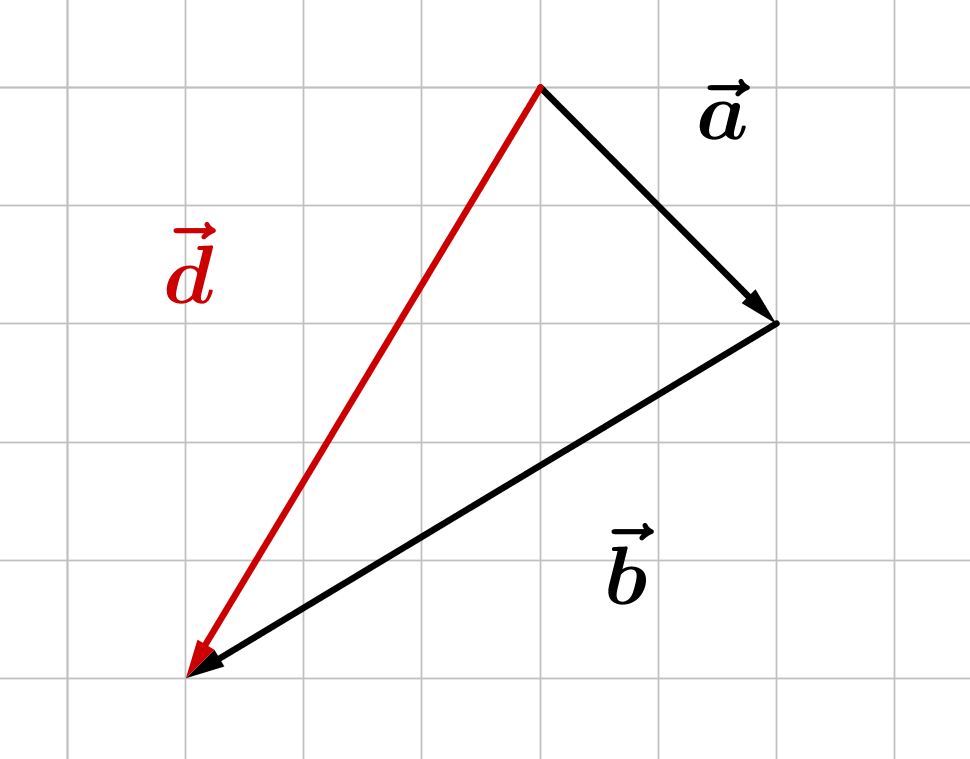
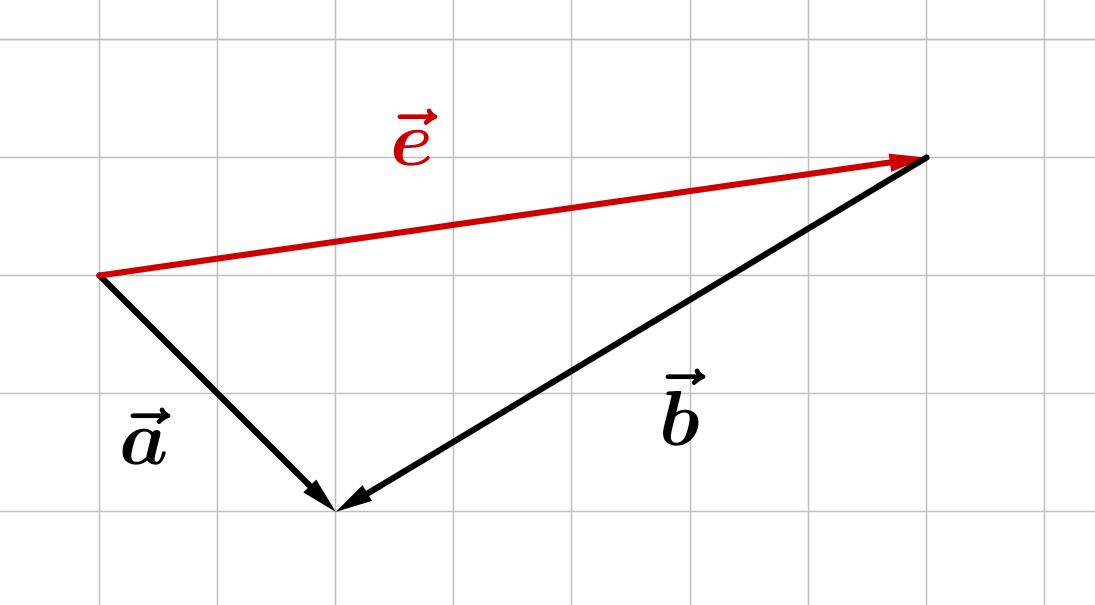
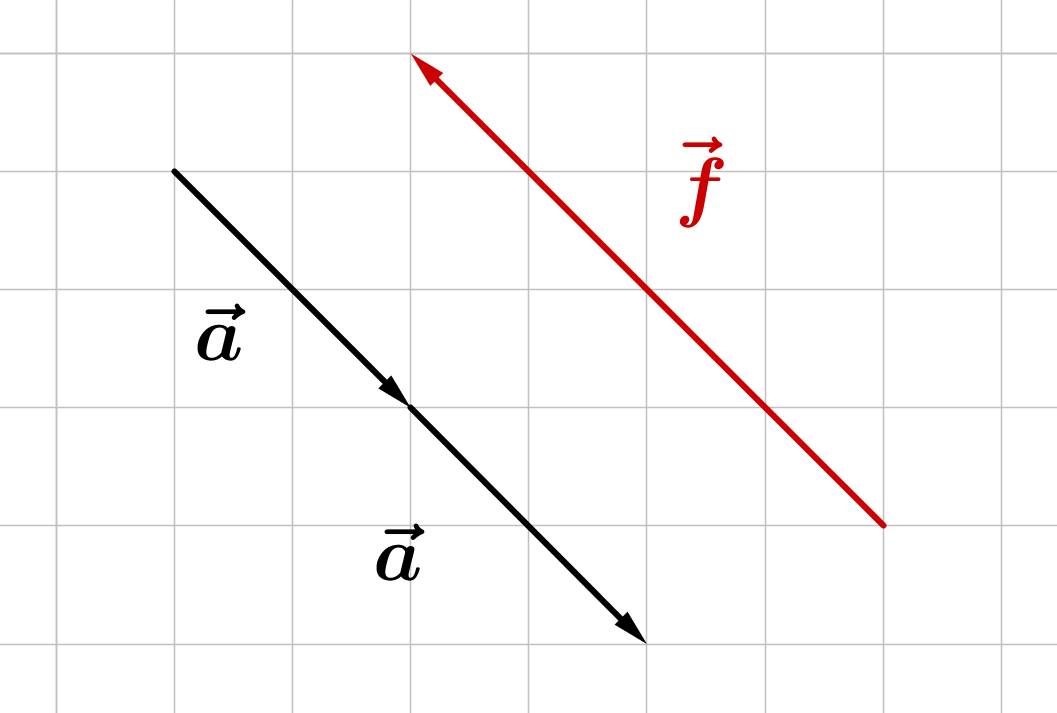
Gegeben sind die Vektoren $\vec{a} = (\begin{array}{c} 2 \\ - 2 \end{array})$ , $\vec{b} = (\begin{array}{c} - 5 \\ - 3 \end{array})$ und $\vec{c} = (\begin{array}{c} 3 \\ 9 \end{array})$ . Berechne jeweils den angegebenen Vektor und veranschauliche in den Teilaufgaben a) bis c) durch eine Zeichnung!
1. $\vec{d} = \vec{a} + \vec{b}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Addition von Vektoren
  geg.: $\vec{a} = (\begin{array}{c} 2 \\ - 2 \end{array})$ , $\vec{b} = (\begin{array}{c} - 5 \\ - 3 \end{array})$
  ges.: $\vec{d} = \vec{a} + \vec{b}$
  Addiere die beiden Vektoren, indem du ihre Koordinaten addierst!
  $\vec{d} = \vec{a} + \vec{b} = (\begin{array}{c} 2 \\ - 2 \end{array}) + (\begin{array}{c} - 5 \\ - 3 \end{array}) =$
  $= (\begin{array}{c} 2 + (- 5) \\ - 2 + (- 3) \end{array}) = (\begin{array}{c} - 3 \\ - 5 \end{array})$
  Grafische Veranschaulichung
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $\vec{e} = \vec{a} - \vec{b}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Subtraktion von Vektoren
  geg.: $\vec{a} = (\begin{array}{c} 2 \\ - 2 \end{array})$ , $\vec{b} = (\begin{array}{c} - 5 \\ - 3 \end{array})$
  ges.: $\vec{e} = \vec{a} - \vec{b}$
  Subtrahiere die beiden Vektoren, indem du ihre Koordinaten subtrahierst!
  $\vec{e} = \vec{a} - \vec{b} = (\begin{array}{c} 2 \\ - 2 \end{array}) - (\begin{array}{c} - 5 \\ - 3 \end{array}) =$
  $= (\begin{array}{c} 2 - (- 5) \\ - 2 - (- 3) \end{array}) = (\begin{array}{c} 7 \\ 1 \end{array})$
  Grafische Veranschaulichung
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $\vec{f} = - 2 \cdot \vec{a}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarmultiplikation von Vektoren
  geg.: $\vec{a} = (\begin{array}{c} 2 \\ - 2 \end{array})$
  ges.: $\vec{f} = - 2 \cdot \vec{a}$
  Multipliziere den Vektor mit $- 2$ , indem du seine Koordinaten mit $- 2$ multiplizierst!
  $\vec{f} = - 2 \cdot \vec{a} = - 2 \cdot (\begin{array}{c} 2 \\ - 2 \end{array}) =$
  $= (\begin{array}{c} - 2 \cdot 2 \\ - 2 \cdot (- 2) \end{array}) = (\begin{array}{c} - 4 \\ 4 \end{array})$
  Grafische Veranschaulichung
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $\vec{g} = \vec{a} - 4 \vec{b} + \frac{2}{3} \vec{c}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektorkette
  geg.: $\vec{a} = (\begin{array}{c} 2 \\ - 2 \end{array})$ , $\vec{b} = (\begin{array}{c} - 5 \\ - 3 \end{array})$ , $\vec{c} = (\begin{array}{c} 3 \\ 9 \end{array})$
  ges.: $\vec{g} = \vec{a} - 4 \vec{b} + \frac{2}{3} \vec{c}$
  Um die Vektorkette zu berechnen, setze zunächst die Koordinaten der Vektoren ein!
  $\vec{g} = (\begin{array}{c} 2 \\ - 2 \end{array}) - 4 \cdot (\begin{array}{c} - 5 \\ - 3 \end{array}) + \frac{2}{3} \cdot (\begin{array}{c} 3 \\ 9 \end{array})$
  Führe nun die Rechenoperationen komponentenweise durch und vereinfache anschließend!
  $\vec{g} = (\begin{array}{c} 2 \\ - 2 \end{array}) - (\begin{array}{c} 4 \cdot (- 5) \\ 4 \cdot (- 3) \end{array}) + (\begin{array}{c} \frac{2}{3} \cdot 3 \\ \frac{2}{3} \cdot 9 \end{array}) =$
  $= (\begin{array}{c} 2 - (- 20) + 2 \\ - 2 - (- 12) + 6 \end{array}) = (\begin{array}{c} 24 \\ 16 \end{array})$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
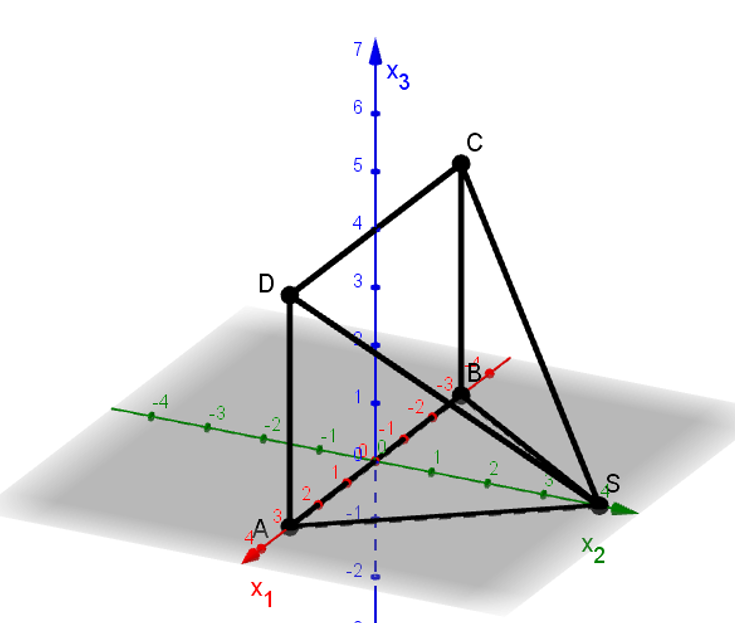
Die liegende Pyramide ABCDS, deren Seitenfläche ABS in der $x_{1} x_{2}$ -Ebene ist und deren rechteckige Grundfläche ABCD in der $x_{1} x_{3}$ -Ebene ist, hat eine Höhe von 4 LE. Dabei ist das Dreieck ABS gleichschenklig mit Basis AB, wobei $| A B | = 6$ gilt und A auf der positiven $x_{1}$ -Achse liegt. Es ist außerdem $B (- 3 | 0 | 0)$ und $D (3 | 0 | 4)$ gegeben.
1. Zeichne die Pyramide in ein dreidimensionales Koordinatensystem und gib die Koordinaten der übrigen Eckpunkte an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Dreidimensionales Koordinatensystem
  Der Punkt B(-3|0|0) ist gegeben und kann direkt eingezeichnet werden.
  Da A auf der positiven $x_{1}$ -Achse liegen soll und einen Abstand von 6 LE zu B haben soll, ist A(3|0|0).
  Da ABS gleichschenklig ist und S ebenfalls in der $x_{1} x_{2}$ -Ebene liegen muss, mit einem Abstand von $4 L E$ , ist S(0|4|0) (auch S(0|-4|0) ist möglich).
  Durch D(3|0|4) wissen wir, dass das Rechteck eine Breite von 4 LE haben muss. Somit ist C(-3|0|4).
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Bestimme das Volumen der Pyramide.
  (VE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
  Für das Volumen einer Pyramide gilt:
  $V = \frac{1}{3} \cdot G \cdot h$
  Mit der rechteckigen Grundfläche also:
  $V = \frac{1}{3} \cdot l \cdot b \cdot h$
  In dieser Pyramide ist die Höhe die Strecke $O S$ , wobei O(0|0|0) der Ursprung ist. Die rechteckige Grundfläche ist durch $A B$ und $A D$ festgelegt.
  Dadurch, dass alle relevanten Seitenlängen parallel zu den Koordinatenachsen sind, können die Werte direkt abgelesen werden:
  $V = \frac{1}{3} \cdot A B \cdot A D \cdot O S = \frac{1}{3} \cdot 6 \cdot 4 \cdot 4 = 32$ (VE)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Untersuche, ob das Dreieck ABS gleichseitig ist, und berechne seinen Flächeninhalt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Länge eines Vektors
  Gleichseitiges Dreieck
  Wäre das Dreieck gleichseitig, so wäre z.B. $A S = A B = 6$ (LE).
  Bestimme die Länge des Vektors $\vec{A S}$ :
  $| \vec{A S} | = | (\begin{array}{c} 0 - 3 \\ 4 - 0 \\ 0 - 0 \end{array}) | = | (\begin{array}{c} - 3 \\ 4 \\ 0 \end{array}) | = \sqrt{(- 3)^{2} + 4^{2} + 0^{2}} = 5$ (LE)
  Somit sind nicht alle Seiten des Dreiecks gleich lang und es ist nicht gleichseitig.
  Flächeninhalt
  Die relevanten Angaben hast du bereits: Die Grundseite $A B = 6$ LE und $O S = 4$ LE.
  Somit ist der Flächeninhalt des Dreiecks:
  $A_{A B S} = \frac{1}{2} \cdot g \cdot h = \frac{1}{2} \cdot A B \cdot O S = \frac{1}{2} \cdot 6 \cdot 4 = 12$ (FE)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Gib die Koordinaten eines beliebigen, weiteren Punktes an, der auf der Kante $A S$ liegt, aber nicht A oder S ist.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektorkette
  Allgemein erfüllt jeder Punkt Q, der zwischen A und S auf der Strecke $A S$ liegt diese Bedingung. Mit einer Vektorkette kann man für $0 < r < 1$ die Ortsvektoren von Q bestimmen durch:
  $\vec{Q} = \vec{A} + r \cdot \vec{A S}$
  Für $r = 0,5$ ergibt sich zum Beispiel:
  $\vec{Q} = (\begin{array}{c} 3 \\ 0 \\ 0 \end{array}) + 0,5 \cdot (\begin{array}{c} - 3 \\ 4 \\ 0 \end{array}) = (\begin{array}{c} 1,5 \\ 2 \\ 0 \end{array})$
  und somit Q(1,5|2|0)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Alle Punkte auf der Strecke $A S$ erfüllen diese Vorgabe.
5. Entscheide, ob der Punkt P, dessen Koordinaten durch $\vec{P} = \vec{A} + \frac{1}{2} \vec{A S} - 0,8 \cdot \vec{S B}$ gegeben sind, innerhalb der Pyramide liegt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektorkette
  Da der Gegenvektor von $\vec{S B}$ verwendet wird, geht man aus dem Dreieck heraus. Somit muss der Punkt außerhalb des Dreiecks liegen.
  Alternativ:
  Bestimme die Koordinaten von P:
  $\vec{P} = (\begin{array}{c} 3 \\ 0 \\ 0 \end{array}) + \frac{1}{2} (\begin{array}{c} - 3 \\ 4 \\ 0 \end{array}) - 0,8 \cdot (\begin{array}{c} - 3 \\ - 4 \\ 0 \end{array}) = (\begin{array}{c} 3,9 \\ 5,2 \\ 0 \end{array})$
  und somit P(3,9|5,2|0)
  Der "Blick von oben" zeigt, dass der Punkt P in $x_{1}$ -Richtung bereits außerhalb des Dreiecks liegt (größter $x_{1}$ -Wert ist bei A der Wert 3) und ebenso in $x_{2}$ -Richtung (größter $x_{2}$ -Wert ist bei S der Wert 4)
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Gemischte Aufgaben

Grafische Veranschaulichung

Hast du eine Frage oder Feedback?

Grafische Veranschaulichung

Hast du eine Frage oder Feedback?

Grafische Veranschaulichung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Gleichseitiges Dreieck

Flächeninhalt

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?