Beschreibe den charakteristischen Verlauf der folgenden Funktionen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
Der charakteristische Verlauf einer Polynomfunktion kann mit ein paar Regeln vorhergesagt werden.
ist eine eine quadratische Funktion, da der größte Exponent ist. Wir wissen, dass das Verhalten im Unendlichen vom Grad des Polynoms, sowie vom Vorzeichen des ersten Koeffizienten (nach Sortierung der Terme nach fallenden Exponenten) abhängt.
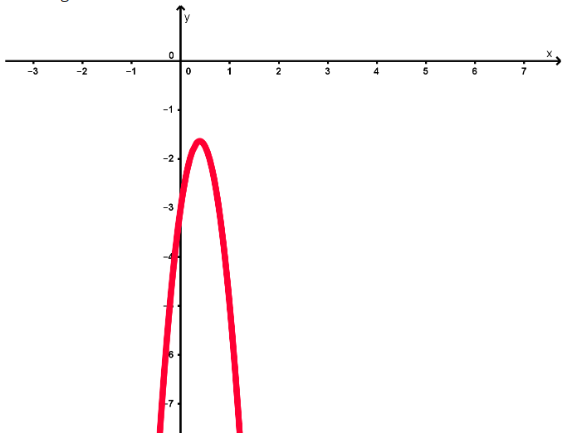
Für sehr kleine Werte von (damit sind negative -Werte mit sehr großem Betrag gemeint), sowie sehr große Werte von dominiert also der Term . Dieser ist negativ für jedes . Damit ist der charakteristische Verlauf der Funktion :
Also ungefähr so:
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
Der charakteristische Verlauf einer Polynomfunktion hängt vom Grad der Polynomfunktion und vom Vorzeichen des Koeffizienten mit dem höchsten vorkommenden Exponenten ab.
Sortiere den Term nach fallenden Exponenten.
Lese den Grad der Funktion und das Vorzeichen des ersten Koeffizienten ab.
Die Funktion hat den Grad und das Vorzeichen des ersten Koeffizienten (nach der Sortierung) ist positiv.
Für sehr kleine Werte von (damit sind negative -Werte mit sehr großem Betrag gemeint), sowie sehr große Werte von dominiert also der Term . Dieser ist positiv für jedes . Damit ist der charakteristische Verlauf der Funktion von links oben nach rechts oben.
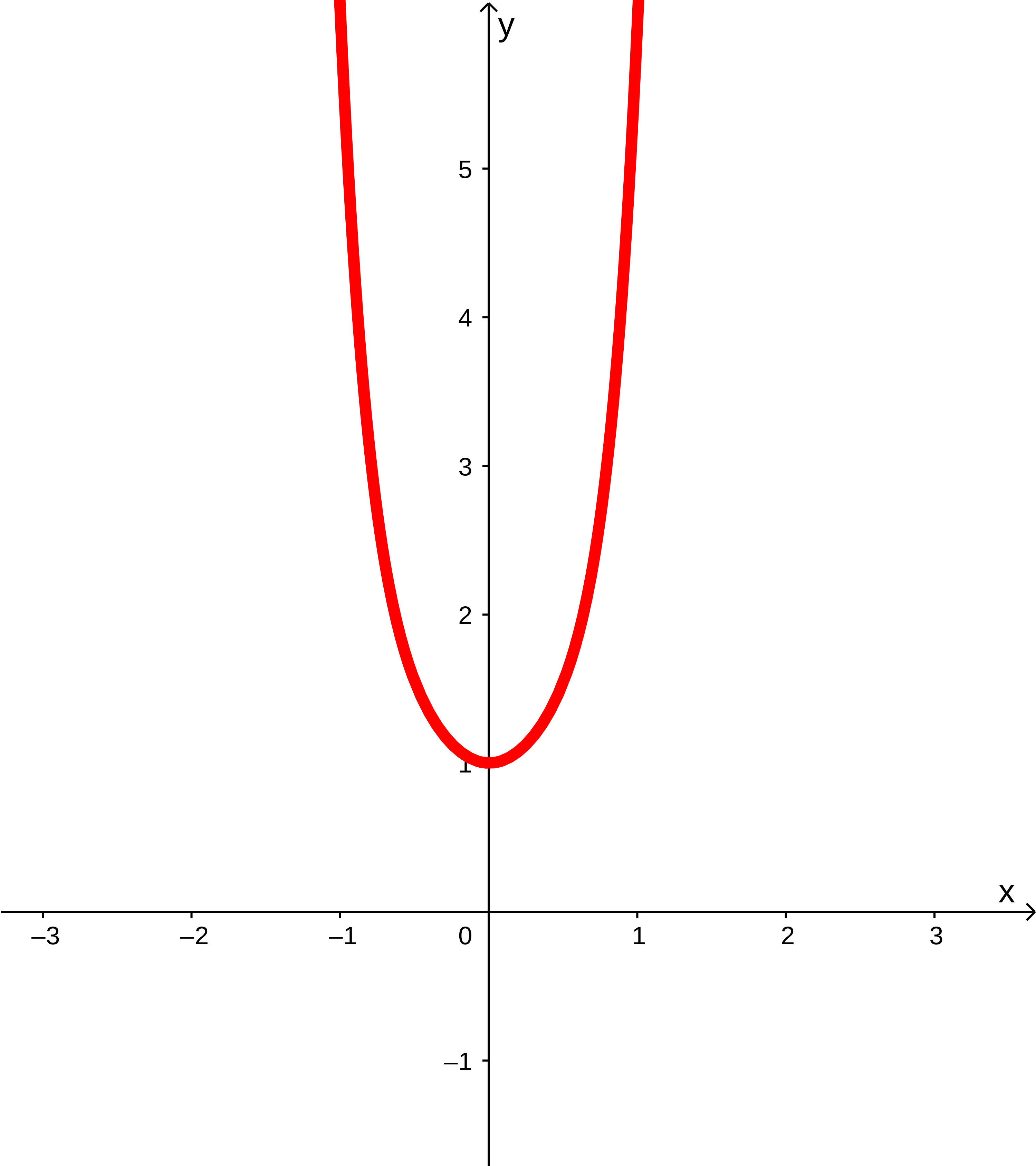
Da die Polynomfunktion nur Potenzen mit geradem Exponenten enthält, ist die Funktion symmetrisch zur y-Achse.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
Der charakteristische Verlauf einer Polynomfunktion hängt vom Grad der Polynomfunktion und vom Vorzeichen des Koeffizienten mit dem höchsten vorkommenden Exponenten ab.
Der Grad der Funktion f(x) ergibt sich aus der Summe der Grade der einzelnen Faktoren.
f ist das Produkt von drei Linearfaktoren. Alle drei Faktoren haben den Grad 1.
Grad
Somit ist f ein Polynom dritten Grades.
In den Faktoren taucht die Variable x zweimal mit positivem Vorzeichen und einmal mit negativem Vorzeichen auf. Das Vorzeichen des Koeffizienten mit dem höchsten vorkommenden Exponenten ist also negativ.
ist positiv, wenn negativ ist und negativ, wenn positiv ist.
Damit ist der charakteristische Verlauf der Funktion von links oben nach rechts unten.
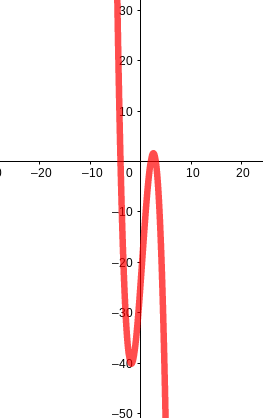
Da die Polynomfuktion sowohl Potenzen mit geradem als auch ungeradem Exponenten enthält, ist die Funktion weder symmetrisch zur y-Achse noch punktsymmetrisch.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
Erste Variante:
Zuerst wird ausmultipliziert.
Jetzt kannst Du die linke und die mittlere Klammer ausmultiplizieren.
Als letztes wird die rechte Klammer multipliziert.
Jetzt hat eine schöne Gestalt, an der der charakteristische Verlauf abgelesen werden kann. Der Grad der Funktion ist . Der Term dominiert also für große Werte von . Da der Koeffizient vor dem gleich ist und selbst positiv ist für alle , hat den charakteristischen Verlauf "Von links oben nach rechts oben".
Zweite Variante (etwas fortgeschrittener):
Zuerst ermittelst Du den Grad dieser Funktion ohne ausmultiplizieren der Terme. Da das Produkt von vier Linearfaktoren ist ( der Faktor hat den Exponenten ) ist ein Polynom vierten Grades. In allen Faktoren taucht die Variable mit positivem Vorzeichen auf. Diese zwei Informationen genügen um den charakteristischen Verlauf von angeben zu können. Dieser ist nämlich "Von links oben, nach rechts oben".
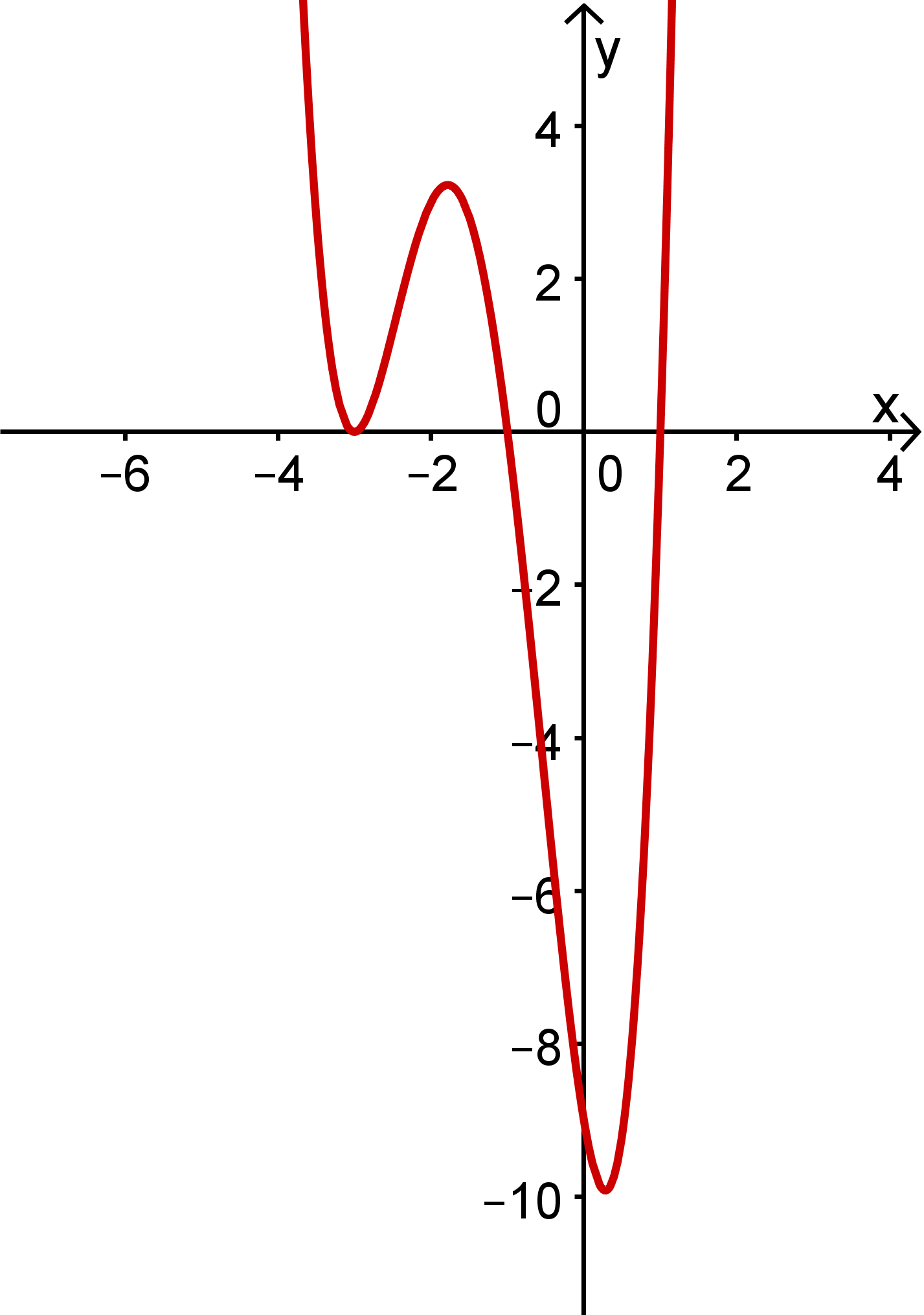
Der Graph von sieht so aus:
(Anmerkung: Das Bild zeigt den "genauen" Verlauf des Graphen von und nicht nur einen ungefähren Verlauf; selbstverständlich kannst du die Einzelheiten (z. B. wie tief der Graph nach unten geht usw.) aus der obigen Betrachtung allein noch nicht wissen.)
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
Bei der Funktion muss man etwas vorsichtiger sein. Es scheint so als wäre in Linearfaktoren zerlegt, doch wenn man genauer hinschaut fällt auf, dass die mittlere Klammer kein Linearfaktor ist. Dort taucht ein auf!
Das ist nicht schlimm. Weil wir aber diese Klammer nicht ausmultiplizieren wollen ( "Mathematiker sind faul" ), musst Du dir ein paar Überlegungen für dieses Polynom machen.
Was solltest Du über zu wissen?
Man braucht ja schließlich den größten Exponenten, der nach ausmultiplizieren der Klammer bleibt. Dieser berechnet sich als das Produkt vom größten Exponenten in der Klammer mit dem Exponenten der Klammer. In unserem Fall wird also , der größte Exponent in sein.
Stellen wir uns das Ausmultiplizieren der Klammer im Kopf vor, so stellen wir fest: Nur indem wir mit sich selbst multiplizieren, erreichen wir die Potenz .
Somit ist der Koeffizient vor dieser Potenz gleich .
Jetzt können wir endlich weiterrechnen :)
Weiter geht's mit
Da das Produkt von drei Funktionen ist, erhalten wir den Grad von indem wir die Grade dieser Funktionen aufsummieren. Der Grad von ist also . Der Koeffizient vor der größten Potenz in ist das Produkt der Koeffizienten vor den größten Potenzen in den einzelnen Faktoren. Wir berechnen also .
Die Funktion sieht also so aus: wobei " … " dafür steht, dass wir Terme mit niedrigeren Exponenten einfach ignorieren.
Da einen geraden Grad hat und ihr erster Koeffizient positiv ist, ist ihr charakteristischer Verlauf "Von links oben nach rechts oben".
Also ungefähr so:

Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
Wir wissen, dass der charakteristische Verlauf einer Polynomfunktion vom Grad der Polynomfunktion und vom Vorzeichen des Koeffizienten mit dem höchsten vorkommenden Exponenten abhängt.
Der Grad der Funktion f(x) ergibt sich aus der Summe der Grade der einzelnen Faktoren.
f ist das Produkt von drei Linearfaktoren. Die ersten beiden Faktoren haben den Grad 1, der dritte Faktor hat den Grad 2.
Grad
Somit ist f ein Polynom vierten Grades.
In den Faktoren taucht die Variable x zweimal mit positivem Vorzeichen und einmal mit negativem Vorzeichen auf. Das Vorzeichen des Koeffizienten mit dem höchsten vorkommenden Exponenten ist also negativ.
ist negativ, wenn negativ ist und negativ, wenn positiv ist.
Damit ist der charakteristische Verlauf der Funktion von links unten nach rechts unten.
Da die Polynomfuktion sowohl Potenzen mit geradem als auch ungeradem Exponenten enthält, ist die Funktion weder symmetrisch zur Y-Achse noch punktsymmetrisch.
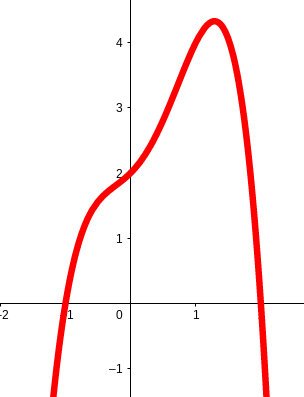
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Verhalten des Graphen einer Polynomfunktion
Tipp: Lass dich vom nicht abschrecken ;) Setze doch mal einen Wert für ein ( z. B. ) und schaue wie der charakteristische Verlauf in diesem Fall wäre. Bleibt der Verlauf dann gleich, wenn man andere Werte für wählt? Lassen sich Aussagen für allgemeinere Werte von machen?
Die Funktion erfordert zusätzliche Überlegungen gegenüber den anderen, denn ist kein fester Wert. Es liegt an uns zu untersuchen, was für verschiedene Werte von mit der Funktion passiert.
Doch bevor wir loslegen, schauen wir uns nochmal genauer an. Der Grad von ist gleich , denn ist immer größer als . Das erspart uns schon mal einiges an Arbeit. Wir wissen ja, dass nur der Teil mit der größten Potenz für den charakteristischen Verlauf von Bedeutung ist.
Wie ist dann der charakteristische Verlauf vom Term ?
Nach dem Ausmultiplizieren des Terms ist der Summand mit dem größten Exponenten Hier müssen wir wirklich unterscheiden, was für verschiedene Werte von passiert.
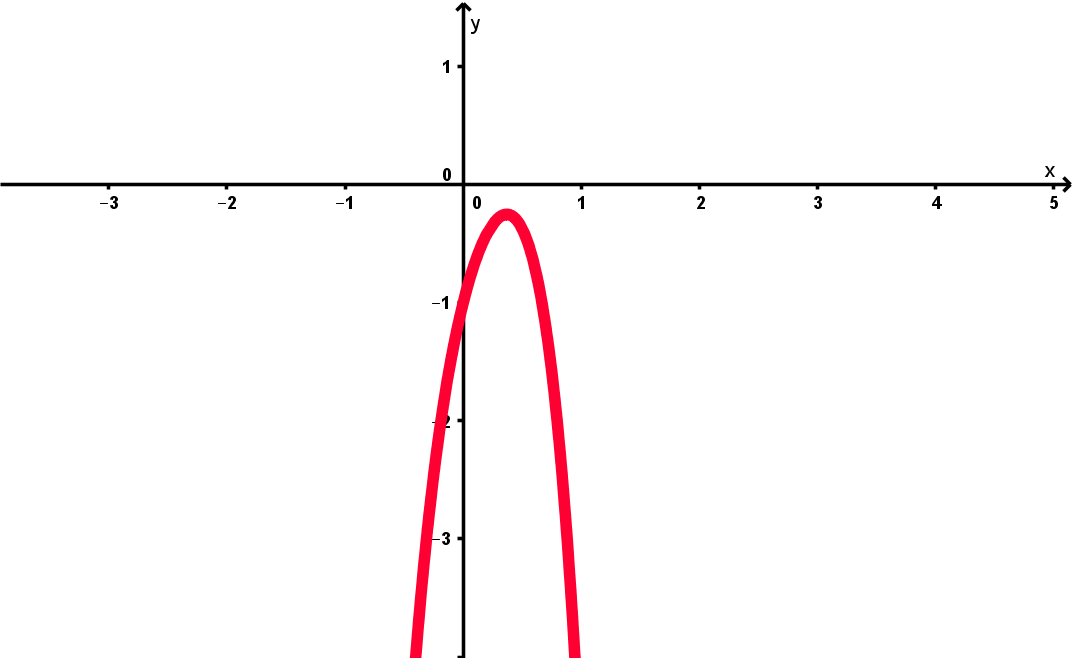
Wenn ungerade ist, dann ist der Exponent gerade. Der Koeffizient vor der größten Potenz von x ist gleich . Somit hat für ungerade den charakteristischen Verlauf "von links unten nach rechts unten".
Also ungefähr so:
Wenn gerade ist, dann ist der Exponent ungerade. Der Koeffizient vor der größten Potenz von x ist weiterhin gleich . Somit ist der charakteristische Verlauf von "von links oben nach rechts unten".
Also ungefähr so:

Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
