Aufgaben zur Kugel

1

Berechne mit den gegebenen Informationen das Volumen der Kugel.

Radius $1\;\text{cm}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen einer Kugel
Für das Volumen einer Kugel gilt:
$V=\frac43r^3\pi$
Setze den Radius $r=1\cm$ ein.
$V=\frac{4}{3}(1{\cm})^3\pi\\=\frac{4}{3}{\pi\cm}^3\\\approx 4{,}2{\cm}^3$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Radius $5\;\text{cm}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen einer Kugel
$r=5{\cm}$
Setze $r$ in die Formel des Kugelvolumens ein.
$V=\frac43\cdot(5\cm)^3\cdot\pi\\\approx523{,}6\cm^3$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Durchmesser $3\;\text{cm}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen einer Kugel
$d=3\cm$
Errechne den Radius $r$ .
$r=\frac12\cdot d\\=\frac12\cdot3\cm\\=1{,}5\cm$
Setze den Radius in die Formel für das Kugelvolumen ein.
$V_{Kugel}=\frac43\cdot r^3\cdot\mathrm\pi\\=\frac43\cdot(1{,}5\cm)^3\cdot\mathrm\pi\\\approx14{,}14 \cm^3$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Umfang $7\;\text{cm}$

Oberfläche $10\cm^2$

2

Berechne mit den gegebenen Informationen die Oberfläche der Kugel.

Radius 1cm

Für diese Aufgabe benötigst Du folgendes Grundwissen: Oberfläche der Kugel berechnen
Radius $r=1\,cm$
Setze den Radius in die Formel für die Oberfläche der Kugel ein.
$O=4\cdot\left(1\,cm\right)^2\cdot\mathrm\pi$
$\approx12{,}566\,cm^2$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Radius 5cm

Für diese Aufgabe benötigst Du folgendes Grundwissen: Oberfläche der Kugel berechnen
Radius $r=5\,cm$
Setze den Radius in die Formel für die Oberfläche der Kugel ein.
$O=4\cdot\left(5\,cm\right)^2\cdot\mathrm\pi$
$\approx314{,}16\,cm^2$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Durchmesser 3cm

Für diese Aufgabe benötigst Du folgendes Grundwissen: Oberfläche der Kugel berechnen
Durchmesser $d=3\,cm$
Bestimme den Radius. Beachte: Der Durchmesser ist doppelt so groß wie der Radius.
$r=3\,cm:2=1{,}5\,cm$
Setze den Radius in die Formel für die Oberfläche der Kugel ein.
$O=4\cdot\left(1{,}5\,cm\right)^2\cdot\mathrm\pi$
$\approx28{,}274\,cm^2$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Volumen $10\mathrm{cm}^3$

Umfang 7cm

3

Berechne mit den gegebenen Informationen den Umfang der Kugel.

Radius $1cm$

Durchmesser $3cm$

Oberfläche $10\mathrm{cm}^2$

Volumen $10\mathrm{cm}^3$

4

Geogebra File: https://assets.serlo.org/legacy/5272_UUQ478PFEk.xml

Berechne in Abhängigkeit von $a$ Volumen und Oberfläche des Rotationskörpers, der durch Rotation der Figur um die Achse $A$ entsteht.

Wie groß muss $a$ sein, damit das Volumen 1 Liter beträgt?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper

Der Rotationskörper $R$ , der durch Drehung der skizzierten Figur um die Achse $A$ entsteht, ist die Kombination eines Kegels mit Höhe $h_{Kegel}=4a$ und Radius $r_{Kegel}=3a$ und einer Halbkugel mit Radius $r_{Halbkugel}=3a$ .

Das Volumen des Rotationskörpers bestimmt sich hier als Summe der Volumina von Kegel und Halbkugel.

Die Oberfläche des Rotationskörpers ist gegeben als Summe der Mantelfächen von Halbkugel und Kegel.

Berechnung des Volumens

Mit den Formeln für das Volumen eines Kegels und das Volumen einer Halbkugel gilt:

$V_R=V_{Kegel}+V_{Halbkugel}= \frac13\cdot r_{Kegel}^2\cdot\pi\cdot h_{Kegel}+\frac23\cdot\pi\cdot r_{Halbkugel}^3$

$V_R=\frac13\cdot(3a)^2\cdot\pi\cdot4a+\frac23\cdot\pi\cdot(3a)^3=12\pi a^3+18\pi a^3=30\pi a^3$

$\Rightarrow$ Das Volumen des Rotationskörpers beträgt also $30\pi a^3$ .

Somit impliziert $V_R=1l=1.000\,cm^3$ folgende Bedingung an $a$ :

$1.000\,cm^3=30\pi a^3\;\Rightarrow\;a^3=\frac{100\,cm^3}{3\pi}\;\Rightarrow a=\sqrt[3]{\frac{100}{3\pi}}\,cm\approx2{,}197\,cm$

Berechnung der Oberfläche

Mit den Formeln für die Mantelfläche eines Kegels und die Mantelfläche einer Halbkugel gilt:

$O_R=M_{Kegel}+M_{Halbkugel}=r_{Kegel}\cdot\pi\cdot s_{Kegel}+2\cdot r_{Halbkugel}^2\cdot\pi$ ,

wobei sich die Mantellinie $s$ als Hypotenuse des rechtwinkligen Dreicks mit Radius und Höhe als Katheten darstellt.

$O_R=3a\cdot\pi\cdot \sqrt{(3a)^2+(4a)^2}+2\cdot(3a)^2\cdot\pi=3a\cdot\pi\cdot5a+18a^2\cdot\pi=33\cdot\pi a^2$

$\Rightarrow$ Die Oberfläche des Rotationskörpers beträgt also $33\pi a^2$ .

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

5

Durch Rotation des dargestellten rot umrandeten Flächenstücks um die Achse $g$ entsteht ein rotationssymmetrischer Körper. Bestimme jeweils das Volumen und den Oberflächeninhalt dieses Rotationskörpers in den Einheiten $a^3$ bzw. $a^2$ .

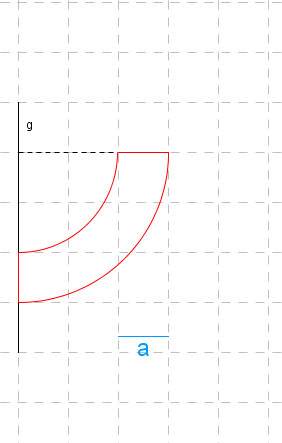
Geogebra File https://assets.serlo.org/legacy/5274\_Ewi8rrrdUJ.xml

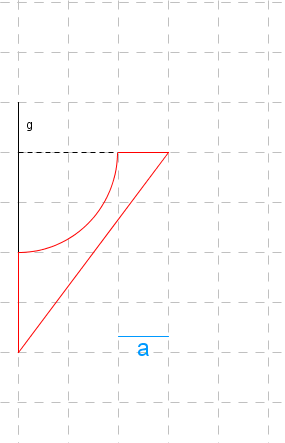
Geogebra File https://assets.serlo.org/legacy/5278\_VpzUZsjU4F.xml

$\displaystyle U$	$=$	$\displaystyle 2\cdot r\cdot\pi$	$\displaystyle :2\pi$
$\displaystyle r$	$=$	$\displaystyle \frac{U}{2\pi}$
	↓	Setze $U=7\cm$ ein.
$\displaystyle r$	$=$	$\displaystyle \frac{7\text{cm}\ }{2\cdot\pi}$
	$≈$	$\displaystyle 1{,}114\ \text{cm}\$

$\displaystyle O$	$=$	$\displaystyle 4r^2\pi$	$\displaystyle :4\pi$
$\displaystyle r^2$	$=$	$\displaystyle \frac{O}{4\pi}$	$\displaystyle \sqrt{ }$
	↓	Ziehe die Quadratwurzel. Da der Radius nur eine positive Zahl sein kann, kannst du das negative Ergebnis vernachlässigen.
$\displaystyle r$	$=$	$\displaystyle \sqrt{\frac{O}{4\pi}}$
	↓	Setze $O=10\cm^2$ ein.
$\displaystyle r$	$=$	$\displaystyle \sqrt{\frac{10\ \text{cm}^2}{4\pi}}$
$\displaystyle r$	$=$	$\displaystyle 0{,}8921\;\text{cm}$

$\displaystyle V$	$=$	$\displaystyle \frac43\cdot r^3\cdot\mathrm\pi$	$\displaystyle :(\frac43\mathrm\pi)$
$\displaystyle r^3$	$=$	$\displaystyle \frac{V\cdot3}{4\cdot\mathrm\pi}$
	↓	Ziehe die Kubikwurzel.
$\displaystyle r$	$=$	$\displaystyle \sqrt[3]{\frac{V\cdot3}{4\cdot\mathrm\pi}}$
	↓	Setze das Volumen ein.
$\displaystyle r$	$=$	$\displaystyle \sqrt[3]{\frac{10\,cm^3\cdot3}{4\cdot\mathrm\pi}}$
	$≈$	$\displaystyle 1{,}3365\,cm$

$\displaystyle U$	$=$	$\displaystyle 2\cdot r\cdot\mathrm\pi$	$\displaystyle :2\mathrm\pi$
$\displaystyle r$	$=$	$\displaystyle \frac U{2\cdot\mathrm\pi}$
	↓	Setze den Umfang ein.
	$=$	$\displaystyle \frac{7\,cm}{2\cdot\mathrm\pi}$
$\displaystyle$	$≈$	$\displaystyle 1{,}1141cm$

$\displaystyle U$	$=$	$\displaystyle 2\pi\cdot r$
	↓	Setze den Radius $r=1\,cm$ ein.
	$=$	$\displaystyle 2\pi\cdot1cm$
	$=$	$\displaystyle 2\pi\ cm$
	$≈$	$\displaystyle 6{,}28\ cm$

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechnung des Volumens

Berechnung der Oberfläche

Lösung zur ersten Figur

Lösung zur zweiten Figur

$\displaystyle d$	$=$	$\displaystyle 3cm$
	↓	Setze den Wert des Durchmessers in die Formel für den Kreisumfang ein.
$\displaystyle U_{Kugel}$	$=$	$\displaystyle 3cm\ \cdot\pi$
	$≈$	$\displaystyle 9{,}42\ cm$

$\displaystyle U$	$=$	$\displaystyle 2\pi\cdot r$
	↓	Füge den Radius $\sqrt{\frac{10}{4\pi}}\mathrm{cm}$ ein.
$\displaystyle U$	$=$	$\displaystyle 2\pi\cdot\sqrt{\frac{10}{4\pi}}\mathrm{cm}$
	$≈$	$\displaystyle 5{,}60\ cm$

$\displaystyle V$	$=$	$\displaystyle \frac{4}{3}\cdot r^3\cdot\pi$	$\displaystyle :\frac{4}{3}\pi\$
$\displaystyle r^3$	$=$	$\displaystyle \frac{V\cdot3}{4\cdot\pi}$	$\displaystyle \sqrt{ }$
	↓	Ziehe die Kubikwurzel
$\displaystyle r$	$=$	$\displaystyle \sqrt[3]{\frac{V\cdot3}{4\cdot\pi\ }}$
	↓	Setze das gegebene Volumen ein.
$\displaystyle r$	$=$	$\displaystyle \sqrt[3]{\frac{10cm^3\cdot3}{4\cdot\mathrm\pi}}$
	$≈$	$\displaystyle 1{,}3365\ cm$
	↓	Berechne den Umfang $\left(U=2\pi\cdot r\right)$ .
$\displaystyle U$	$≈$	$\displaystyle 2\pi\ \cdot1{,}3365\ cm$
	$≈$	$\displaystyle 8{,}397\ cm$

$\displaystyle V_{rot}$	$=$	$\displaystyle V_{außen}-V_{innen}$
	↓	Subtrahiere das innere Volumen vom äußeren.
	$=$	$\displaystyle \frac{2}{3}\cdot(3a)^3\cdot\mathrm{\pi}-\frac{2}{3}\cdot(2\mathrm{a})^3\cdot\mathrm{\pi}$
	↓	Löse auf.
	$=$	$\displaystyle 2\mathrm{\pi}\cdot27\mathrm{a}^3-\frac{2}{3}\mathrm{\pi}\cdot8\mathrm{a}^3$
	↓	Vereinfache so weit wie möglich
	$=$	$\displaystyle \frac{2}{3}\mathrm{\pi}\cdot19\mathrm{a}^3$
	$=$	$\displaystyle \frac{38}{3}\mathrm{\pi a}^3$