Aufgaben zu Rotationskörpern

Schaffst du es, Volumen und Oberflächen von Rotationskörpern zu berechnen? Teste dich mit diesen gemischten Aufgaben!

1
raschweb.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch
Ein rotationssymmetrisches Werkstück soll aus Gusseisen der Dichte $7{,}2\frac g{cm^3}$ hergestellt werden.
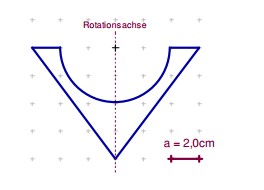
Das Bild zeigt das Werkstück im Querschnitt. Berechne die Masse des Werkstücks.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenberechnung
Gesucht: Masse $m$ des Werkstücks
Die Masse $m$ hängt mit dem Volumen $V$ und der Dichte $\rho$ zusammen.
Die Formel lautet: $\rho=\dfrac{m}{V}$
Stelle diese Formel nach $m$ um.
$m=\rho \cdot V$
$\rho =7{,}2 \frac {\mathrm {g}}{\mathrm{cm}^3}$ ist in der Aufgabe angegeben. Das Volumen musst du noch berechnen.
Berechnung des Volumens
Das Werkstück ist rotationssymmetrisch. Wenn sich die Figur um die eingezeichnete Achse dreht, entsteht
ein Kegel (wegen des Dreiecks),
aus dem eine Halbkugel (wegen des Halbkreises) herausgeschnitten ist.
Ziehe also das Volumen der halben Kugel von dem Volumen des Kegels ab.
$V=\frac13\cdot\left(6{,}0cm\right)^2\mathrm\pi\cdot8{,}0\mathrm{cm}-\frac12\cdot\frac43\cdot\left(4{,}0\mathrm{cm}\right)^3\mathrm\pi\\=(\frac{160}3\cdot\pi)\mathrm{cm}^3\\\approx168\mathrm{cm}^3$
Berechnung der Masse
$m=\rho\cdot V=7{,}2\frac{g}{cm^3}\cdot168cm^3=1209{,}6g\approx1{,}2kg$
2
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Die nebenstehende Figur rotiert um die Achse A.
Berechne das Volumen des Rotationskörpers in Abhängigkeit von a.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
Durch die Rotation entsteht ein Kegel auf einem großen Zylinder, aus dem ein Kleinerer ausgeschnitten wurde.
${\mathrm V}_\mathrm{Rotationskörper}=\;{\mathrm V}_{\mathrm{großer}\;\mathrm{Zylinder}}-\;{\mathrm V}_{\mathrm{kleiner}\;\mathrm{Zylinder}}+\;{\mathrm V}_\mathrm{Kegel}$
Setze die bekannten Größen in die allgemeine Volumenformel des Kegels ein.
$\def\arraystretch{1.25} \begin{array}{l}{\mathrm V}_{\mathrm{Kegel}\;}=\frac13\cdot\;({\mathrm r}_\mathrm{Kegel})^2\cdot\mathrm\pi\cdot{\mathrm h}_\mathrm{Kegel}\\\;\;\;\;\;\;\;\;\;\;\;=\;\frac13\;\cdot\;(2\mathrm a)^2\;\cdot\mathrm\pi\cdot\mathrm a\\\;\;\;\;\;\;\;\;\;\;\;=\;\frac13\cdot4\mathrm a^2\cdot\mathrm\pi\cdot\mathrm a\\\;\;\;\;\;\;\;\;\;\;\;=\frac43\mathrm a^3\cdot\mathrm\pi\end{array}$
Setze die bekannten Größen in die allgemeine Volumenformel des Zylinders ein.
$\def\arraystretch{1.25} \begin{array}{l}{\mathrm V}_{\mathrm{großer}\;\mathrm{Zylinder}}=\;({\mathrm r}_{\mathrm{großer}\;\mathrm{Zylinder}})^2\;\cdot\mathrm\pi\cdot{\mathrm h}_{\mathrm{großer}\;\mathrm{Zylinder}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\;(2\mathrm a)^2\cdot\mathrm\pi\cdot\mathrm a\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\;4\mathrm a^2\cdot\mathrm\pi\cdot\mathrm a\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\;4\mathrm a^3\cdot\mathrm\pi\end{array}$
$\def\arraystretch{1.25} \begin{array}{l}{\mathrm V}_{\mathrm{kleiner}\;\mathrm{Zylinder}}=\;({\mathrm r}_{\mathrm{kleiner}\;\mathrm{Zylinder}})^2\cdot\mathrm\pi\cdot{\mathrm h}_{\mathrm{kleiner}\;\mathrm{Zylinder}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\;\mathrm a^2\;\cdot\mathrm\pi\cdot\mathrm a\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\;\mathrm a^3\;\cdot\mathrm\pi\end{array}$
Führe alle Ergebnisse in die ursprüngliche Gleichung zusammen.
$\def\arraystretch{1.25} \begin{array}{l}{\mathrm V}_\mathrm{Rotationskörper}=\;4\mathrm a^3\cdot\mathrm\pi\;-\;\mathrm a^3\cdot\mathrm\pi\;+\;\frac43\cdot\mathrm a^3\cdot\mathrm\pi\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\;4\frac13\cdot\mathrm a^3\cdot\mathrm\pi\end{array}$
3
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Berechne in Abhängigkeit von $a$ Volumen und Oberfläche des Rotationskörpers, der durch Rotation der Figur um die Achse $A$ entsteht.
Wie groß muss $a$ sein, damit das Volumen 1 Liter beträgt?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
Der Rotationskörper $R$ , der durch Drehung der skizzierten Figur um die Achse $A$ entsteht, ist die Kombination eines Kegels mit Höhe $h_{Kegel}=4a$ und Radius $r_{Kegel}=3a$ und einer Halbkugel mit Radius $r_{Halbkugel}=3a$ .
Das Volumen des Rotationskörpers bestimmt sich hier als Summe der Volumina von Kegel und Halbkugel.
Die Oberfläche des Rotationskörpers ist gegeben als Summe der Mantelfächen von Halbkugel und Kegel.
Berechnung des Volumens
Mit den Formeln für das Volumen eines Kegels und das Volumen einer Halbkugel gilt:
$V_R=V_{Kegel}+V_{Halbkugel}= \frac13\cdot r_{Kegel}^2\cdot\pi\cdot h_{Kegel}+\frac23\cdot\pi\cdot r_{Halbkugel}^3$
$V_R=\frac13\cdot(3a)^2\cdot\pi\cdot4a+\frac23\cdot\pi\cdot(3a)^3=12\pi a^3+18\pi a^3=30\pi a^3$
$\Rightarrow$ Das Volumen des Rotationskörpers beträgt also $30\pi a^3$ .
Somit impliziert $V_R=1l=1.000\,cm^3$ folgende Bedingung an $a$ :
$1.000\,cm^3=30\pi a^3\;\Rightarrow\;a^3=\frac{100\,cm^3}{3\pi}\;\Rightarrow a=\sqrt[3]{\frac{100}{3\pi}}\,cm\approx2{,}197\,cm$
Berechnung der Oberfläche
Mit den Formeln für die Mantelfläche eines Kegels und die Mantelfläche einer Halbkugel gilt:
$O_R=M_{Kegel}+M_{Halbkugel}=r_{Kegel}\cdot\pi\cdot s_{Kegel}+2\cdot r_{Halbkugel}^2\cdot\pi$ ,
wobei sich die Mantellinie $s$ als Hypotenuse des rechtwinkligen Dreicks mit Radius und Höhe als Katheten darstellt.
$O_R=3a\cdot\pi\cdot \sqrt{(3a)^2+(4a)^2}+2\cdot(3a)^2\cdot\pi=3a\cdot\pi\cdot5a+18a^2\cdot\pi=33\cdot\pi a^2$
$\Rightarrow$ Die Oberfläche des Rotationskörpers beträgt also $33\pi a^2$ .

Durch Rotation des dargestellten rot umrandeten Flächenstücks um die Achse $g$ entsteht ein rotationssymmetrischer Körper. Bestimme jeweils das Volumen und den Oberflächeninhalt dieses Rotationskörpers in den Einheiten $a^{3}$ bzw. $a^{2}$ .

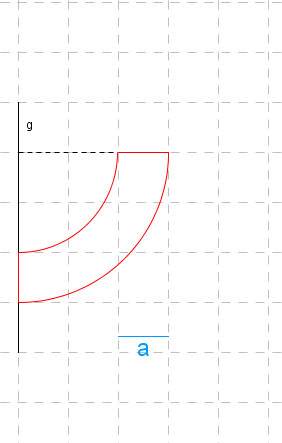
Geogebra File https://assets.serlo.org/legacy/5274\_Ewi8rrrdUJ.xml

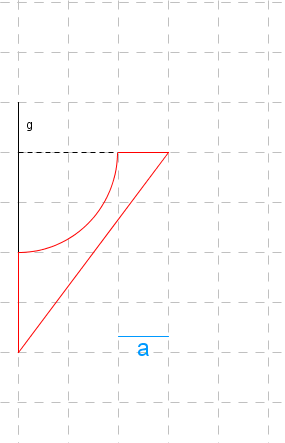
Geogebra File https://assets.serlo.org/legacy/5278\_VpzUZsjU4F.xml

5
Zeichne einen Axialschnitt für den Rotationskörper.
Maße: $r=3\;\text{cm}$ ;
$h_1=h_2=h_3=4\;\text{cm}$

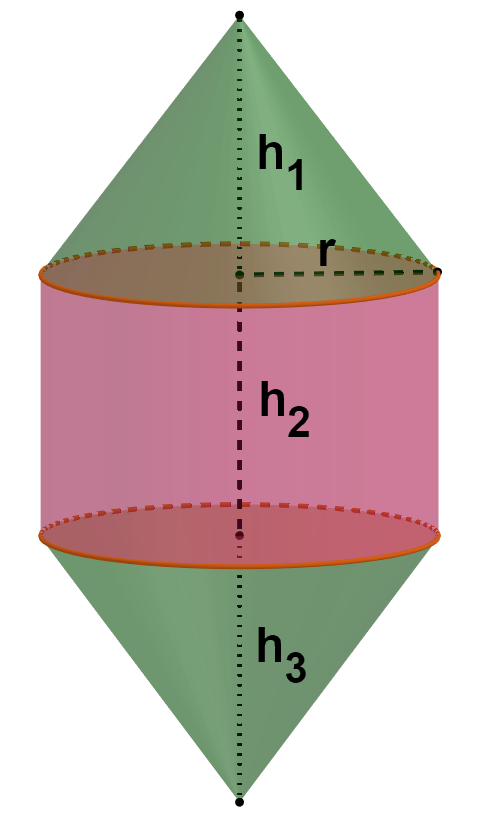
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
Der zusammengesetzte Körper besteht aus zwei gleich großen Kegeln und einem Zylinder.
Axialschnitt des Zylinders
Der Zylinder hat einen Radius von $r= 3 \;\text{cm}$ und eine Höhe von $h=4 \;\text{cm}$ .
Zeichne zunächst die Symmetrieachse $s$ als senkrechte Gerade.
Der Axialschnitt eines Zylinders ist ein Rechteck.
Dieses Rechteck hat die Maße:
$\overline{AB}=2\cdot r=6 \;\text{cm}$ und $\overline{BC}=h=4 \;\text{cm}$ .
Zeichne ein Rechteck mit den angegebenen Maßen symmetrisch zur Symmetrieachse.
Die Gerade $s$ schneidet die beiden Strecken $\left[DC\right]$ und $\left[AB\right]$ in den Punkten $I$ und $J$ .
Axialschnitt des Kegels
Die Höhe $h$ des gleichschenkligen Dreiecks ist:
$h=4 \;\text{cm}$ .
Zeichne um $I$ einen Kreis mit dem Radius $r=4 \;\text{cm}$ . Der Kreis schneidet die Gerade $s$ im Punkt $F$ . Verbinde den Punkt $D$ mit $F$ und den Punkt $C$ ebenfalls mit $F$ .
Der Axialschnitt des ersten Kegels ist fertig.
Zur besseren Übersichtlichkeit werden einige Hilfslinien und Punkte entfernt.
Den Axialschnitt des zweiten Kegels konstruierst du entsprechend.
Dein Axialschnitt ist fertig.
Bei dem dargestellten Körper handelt es sich um einen Rotationskörper. Die Achse, um die sich die Figur dreht, nennt man Rotationsachse. Schneidet man einen Rotationskörper längs seiner Achse durch, erhält man den Axialschnitt des Körpers.
6
Die abgebildeten Figuren rotieren um die eingezeichnete Achse $s$ . Beschreibe den Rotationskörper der dann entsteht.
1. Maße:
  Kreisradius $r= 4\;\text{cm}$
  Basis des Dreiecks $4\;\text{cm}$
  Höhe des Dreiecks $h= 4{,}5\;\text{cm}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
  Der rotierende Kreis ergibt eine Kugel, bei der allerdings ein Kugelsegment mit dem Radius $r'=2\;\text{cm}$ fehlt. (Der verbleibende Rest der Kugel ist allerdings auch ein Kugelsegment.)
  Das rotierende gleichschenklige Dreieck ergibt einen Kegel mit dem Durchmesser $d= 4\;\text{cm}$ und der Höhe $h= 4{,}5\;\text{cm}$ .
  Der Kegel sitzt sozusagen etwas innerhalb der Kugel.
  Zur Veranschaulichung:
  Bild des Rotationskörpers.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Maße:
  entsprechend der Zeichnung
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
  Der um die Achse $s$ rotierende kleine Halbkreis mit dem Radius $r_2= 1\;\text{cm}$ ergibt eine Halbkugel mit dem gleichen Radius. Der rotierende große Halbkreis mit dem Radius $r_1= 5\;\text{cm}$ ergibt eine Halbkugel mit dem gleichen Radius.
  Das Trapez zwischen den beiden Halbkreisen ergibt bei Rotation um die Achse $s$ einen Kegelstumpf der Höhe $h= 4\;\text{cm}$ mit einem Grundkreisradius $r_1= 5\;\text{cm}$ und einer Deckfläche mit dem Radius $r_2= 1\;\text{cm}$ .
  Zur Veranschaulichung:
  Bild des Rotationskörpers (um $90^\circ$ gedreht).
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7
Gegeben ist ein Rotationskörper. Welches Bild stellt seinen Axialschnitt dar?
Bild 1
Bild 2
Bild 3
Bild 4
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
Der Rotationskörper
Der gegebene Rotationskörper besteht aus einer $\textcolor{cc0000}{\text{Halbkugel (rot)}}$ (untere Hälfte der Kugel) und einem $\textcolor{660099}{\text{Kegelstumpf (lila)}}$ .
Die Axialschnitte
In den vier Bildern sind folgende geometrische Figuren enthalten:
zwei gleichschenklige Dreiecke, zwei gleichschenklige Trapeze, drei Halbkreise und ein Kreissegment.
Die folgende Tabelle zeigt die Zuordnung zwischen einem Axialschnitt und dem dazugehörenden Rotationskörper.
Axialschnitt
Rotationskörper
gleichschenkliges Dreieck
Kegel
gleichschenkliges Trapez
Kegelstumpf
Halbkreis
Halbkugel
Kreissegment
Kugelsegment
Bild 1:
Dieser Axialschnitt besteht aus einem Halbkreis und einem gleichschenkligen Dreieck.
Der Rotationskörper besteht somit aus einer Halbkugel und aus einem Kegel.
Deshalb kann es nicht der Axialschnitt des gegebenen Rotationskörpers sein.
Bild 2:
Dieser Axialschnitt besteht aus einem Halbkreis und aus einem gleichschenkligen Trapez.
Der Rotationskörper besteht somit aus einer Halbkugel (untere Hälfte der Kugel) und aus einem Kegelstumpf.
Der Axialschnitt gehört zu dem gegebenen Rotationskörper.
Bild 3:
Dieser Axialschnitt besteht aus einem Halbkreis und aus einem gleichschenkligen Trapez.
Der Rotationskörper besteht somit aus einer Halbkugel und aus einem Kegelstumpf.
Der Axialschnitt passt nicht zu dem gegebenen Rotationskörper, da die Halbkugel die obere Hälfte der Kugel ist.
Deshalb ist es nicht der gegebene Rotationskörper.
Bild 4:
Dieser Axialschnitt besteht aus einem Kreissegment und einem gleichschenkligen Dreieck .
Der Rotationskörper besteht somit aus einem Kugelsegment und aus einem Kegel.
Deshalb ist es nicht der gegebene Rotationskörper.
8
Gegeben ist ein Rotationskörper. Welches Bild stellt seinen Axialschnitt dar?
Bild 1
Bild 2
Bild 3
Bild 4
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
Der Rotationskörper
Der gegebene Rotationskörper besteht aus einem $\textcolor{cc0000}{\text{Kegelstumpf (rot)}}$ und einem $\textcolor{660099}{\text{Kegel (lila)}}$ . Dabei ist der Grundflächenradius des Kegelstumpfes nur wenig größer als der Deckflächenradius. Der Deckflächenradius des Kegelstumpfes ist gleichzeitig der Kegelradius.
Die Axialschnitte
In den vier Bildern sind folgende geometrische Figuren enthalten:
(mehrere) gleichschenklige Dreiecke, ein Rechteck, (mehrere) gleichschenklige Trapeze und ein Kreissegment.
Die folgende Tabelle zeigt die Zuordnung zwischen einem Axialschnitt und dem dazugehörenden Rotationskörper.
Axialschnitt
Rotationskörper
gleichschenkliges Dreieck
Kegel
gleichschenkliges Trapez
Kegelstumpf
Rechteck
Zylinder
Kreissegment
Kugelsegment
Bild 1:
Dieser Axialschnitt besteht aus einem Rechteck und einem gleichschenkligen Dreieck.
Der Rotationskörper besteht somit aus einem Zylinder und aus einem Kegel.
Deshalb kann es nicht der Axialschnitt des gegebenen Rotationskörpers sein.
Bild 2:
Dieser Axialschnitt besteht aus einem Kreissegment und einem gleichschenkligen Dreieck.
Der Rotationskörper besteht somit aus einem Kugelsegment und aus einem Kegel.
Deshalb ist es nicht der gegebene Rotationskörper.
Bild 3:
Dieser Axialschnitt besteht aus einem gleichschenkligen Trapez und einem gleichschenkligen Dreieck.
Der Rotationskörper besteht somit aus einem Kegelstumpf und aus einem Kegel.
Der Axialschnitt passt zu dem gegebenen Rotationskörper. Der Radius der Deckfläche des Kegelstumpfs steht im richtigen Verhältnis zum Radius der Grundfläche des Kegelstumpfs.
Deshalb ist es der gegebene Rotationskörper.
Bild 4:
Dieser Axialschnitt besteht aus einem gleichschenkligen Trapez und einem gleichschenkligen Dreieck.
Der Rotationskörper besteht somit aus einem Kegelstumpf und aus einem Kegel.
Der Axialschnitt passt zu dem gegebenen Rotationskörper. Allerdings ist der Radius der Grundfläche des Kegelstumpfs viel zu klein im Vergleich zum Radius der Deckfläche des Kegelstumpfs.
Deshalb ist es nicht der gegebene Rotationskörper.
9
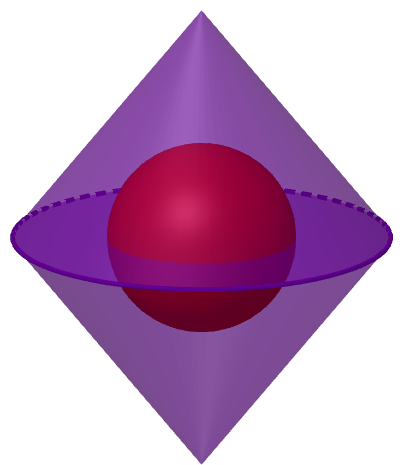
Gegeben ist ein Rotationskörper.
Zeichne seinen Axialschnitt.
Maße:
Kugelradius: $r_{\circ} = 2\;\text{cm}$ ,
Kegelradius: $r_{\triangle}= 4\;\text{cm}$ ,
Kegelhöhe: $h= 5\;\text{cm}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
Der Rotationskörper
Der gegebene Rotationskörper besteht aus zwei $\textcolor{660099}{\text{Kegeln (lila)}}$ , deren Grundflächen aufeinander liegen. Im Mittelpunkt des Rotationskörpers befindet sich eine $\textcolor{cc0000}{\text{Kugel (rot)}}$ .
Der Axialschnitt
Die folgende Tabelle zeigt die Zuordnung zwischen einem Rotationskörper und dem dazugehörenden Axialschnitt.
Rotationskörper
Axialschnitt
Kegel
gleichschenkliges Dreieck
Kugel
Kreis
Axialschnitt der Kugel
Zeichne zunächst die Symmetrieachse $s$ als senkrechte Gerade.
Wähle einen Punkt $M$ auf dieser Geraden. Dieser Punkt ist der Mittelpunkt des Kreises (Axialschnitt der Kugel).
Zeichne einen Kreis um $M$ mit dem Radius $r_{\circ} = 2\;\text{cm}$ .
Axialschnitt des Doppelkegels
Jeder der beiden Kegel hat einen Radius von $r_{\triangle}= 4\;\text{cm}$ und eine Höhe von $h=5 \;\text{cm}$ . Als Axialschnitt musst du zwei gleichschenklige Dreiecke zeichnen.
Konstruiere zuerst die Basis der beiden gleichschenkligen Dreiecke.
Zeichne eine Gerade $g$ senkrecht zur Symmetrieachse $s$ durch den Punkt $M$ .
Zeichne um $M$ einen Kreis mit dem Radius $r_{\triangle}= 4\;\text{cm}$ (das ist der Kegelradius). Der Kreis schneidet die Gerade $g$ in den Punkten $A$ und $B$ .
Die Strecke $\left[{AB}\right]$ ist die Basis der beiden gleichschenkligen Dreiecke.
Zur besseren Übersichtlichkeit werden einige Hilfslinien entfernt.
Konstruktion der Höhe der beiden gleichschenkligen Dreiecke.
Zeichne um $M$ einen Kreis mit dem Radius $r=5 \;\text{cm}$ (das ist die Kegelhöhe).
Der Kreis schneidet die Symmetrieachse $s$ in den Punkten $C$ und $D$ . Verbinde $A$ mit $C$ und $B$ mit $C$ . Verbinde ebenso $A$ mit $D$ und $B$ mit $D$ .
Im Axialschnitt ist der Teil der Strecke $\left[{AB}\right]$ nicht sichtbar, der durch die Kugel verläuft. Außerdem werden zur besseren Übersichtlichkeit alle Hilfslinien und Punkte entfernt.
Der Axialschnitt des Rotationskörpers ist fertig.
Bei dem dargestellten Körper handelt es sich um einen Rotationskörper. Die Achse, um die sich die Figur dreht, nennt man Rotationsachse. Schneidet man einen Rotationskörper längs seiner Achse durch, erhält man den Axialschnitt des Körpers.

Axialschnitt	Rotationskörper
gleichschenkliges Dreieck	Kegel
gleichschenkliges Trapez	Kegelstumpf
Halbkreis	Halbkugel
Kreissegment	Kugelsegment

Axialschnitt	Rotationskörper
gleichschenkliges Dreieck	Kegel
gleichschenkliges Trapez	Kegelstumpf
Rechteck	Zylinder
Kreissegment	Kugelsegment

Rotationskörper	Axialschnitt
Kegel	gleichschenkliges Dreieck
Kugel	Kreis

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle V_{rot}$	$=$	$\displaystyle V_{außen}-V_{innen}$
	↓	Subtrahiere das innere Volumen vom äußeren.
	$=$	$\displaystyle \frac{2}{3}\cdot(3a)^3\cdot\mathrm{\pi}-\frac{2}{3}\cdot(2\mathrm{a})^3\cdot\mathrm{\pi}$
	↓	Löse auf.
	$=$	$\displaystyle 2\mathrm{\pi}\cdot27\mathrm{a}^3-\frac{2}{3}\mathrm{\pi}\cdot8\mathrm{a}^3$
	↓	Vereinfache so weit wie möglich
	$=$	$\displaystyle \frac{2}{3}\mathrm{\pi}\cdot19\mathrm{a}^3$
	$=$	$\displaystyle \frac{38}{3}\mathrm{\pi a}^3$

$\displaystyle V_{rot}$	$=$	$\displaystyle V_{außen}-V_{innen}$
	↓	Subtrahiere das innere Volumen vom äußerem
	$=$	$\displaystyle \frac{1}{3}(3a)^2\mathrm{\pi}(4\mathrm{a})-\frac{2}{3}\cdot(2\mathrm{a})^3\mathrm{\pi}$
	↓	Löse die Klammer auf
	$=$	$\displaystyle \frac{1}{3}\cdot9a^2\mathrm{\pi}\cdot4\mathrm{a}-\frac{2}{3}\cdot8\mathrm{a}^3\mathrm{\pi}$
	↓	Multipliziere die Faktoren
	$=$	$\displaystyle 3\mathrm{a}^2\mathrm{\pi}\cdot4\mathrm{a}-\frac{2}{3}\cdot8\mathrm{a}^3\mathrm{\pi}$
	↓	Klammere a und $\mathrm\pi$ aus
	$=$	$\displaystyle (3\cdot4-\frac{2}{3}\cdot8)\cdot\mathrm{\pi a}^2\mathrm{a}$
	↓	Löse auf
	$=$	$\displaystyle (12-\frac{16}{3})\cdot\mathrm{\pi a}^2\mathrm{a}$
	$=$	$\displaystyle \frac{20}{3}\mathrm{\pi a}^3$

Aufgaben zu Rotationskörpern

Berechnung des Volumens

Berechnung der Masse

Berechnung des Volumens

Berechnung der Oberfläche

Lösung zur ersten Figur

Lösung zur zweiten Figur

Axialschnitt des Zylinders

Axialschnitt des Kegels

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Der Rotationskörper

Die Axialschnitte

Der Rotationskörper

Die Axialschnitte

Der Rotationskörper

Der Axialschnitt

Axialschnitt der Kugel

Axialschnitt des Doppelkegels