Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Gemischte Aufgaben zur Addition und skalaren Multiplikation

  1. 1

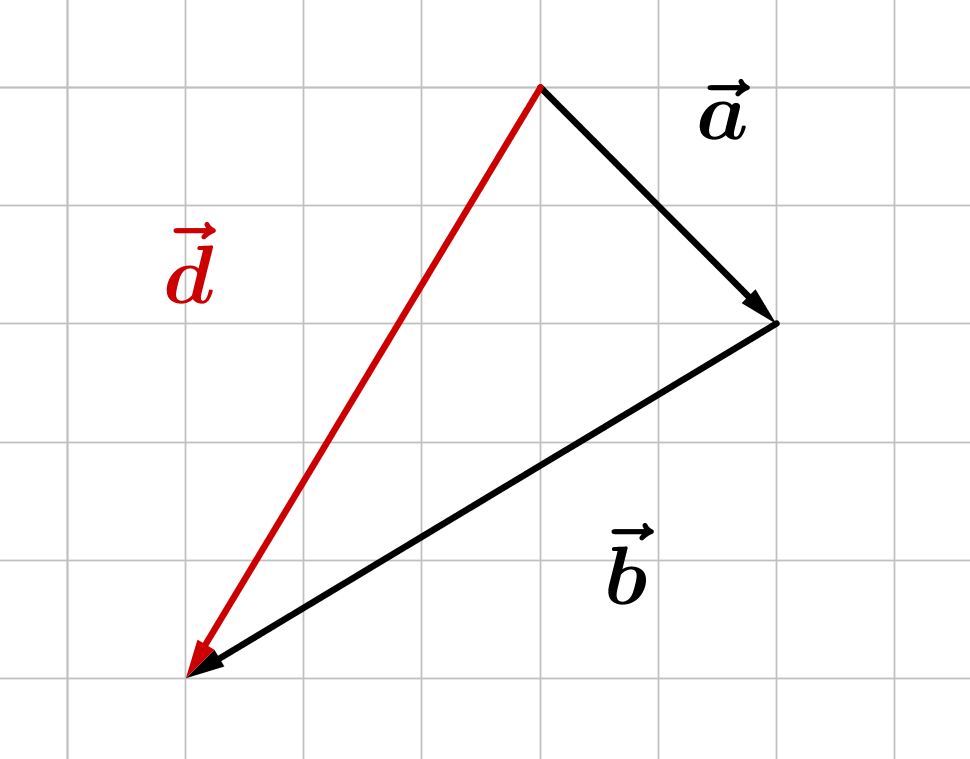
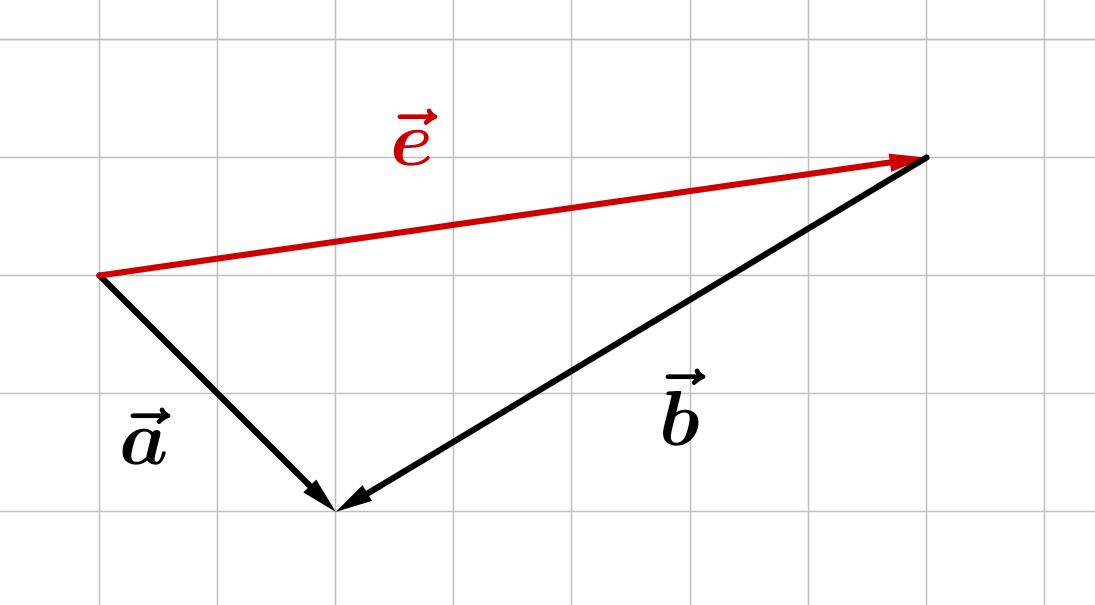
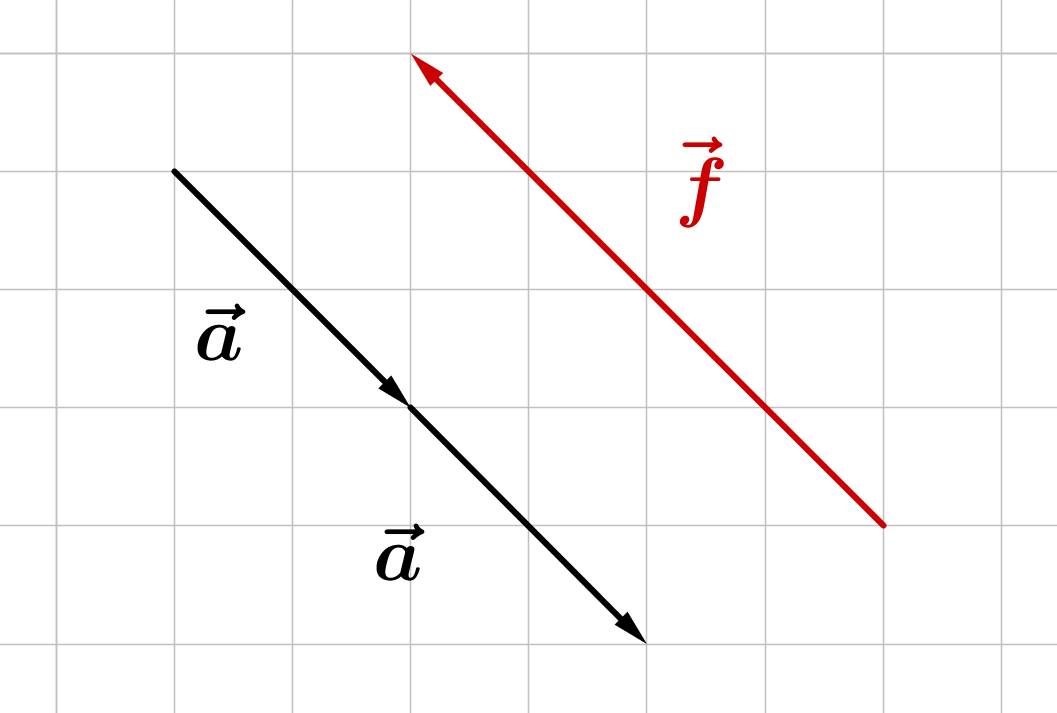
    Gegeben sind die Vektoren a⃗=(2−2)\vec a = \begin{pmatrix}2\\-2\end{pmatrix}, b⃗=(−5−3)\vec b = \begin{pmatrix}-5\\-3\end{pmatrix} und c⃗=(39)\vec c = \begin{pmatrix}3\\9\end{pmatrix}. Berechne jeweils den angegebenen Vektor und veranschauliche in den Teilaufgaben a) bis c) durch eine Zeichnung!

    1. d⃗=a⃗+b⃗\displaystyle \vec d = \vec a + \vec b
    2. e⃗=a⃗−b⃗\displaystyle \vec e = \vec a - \vec b
    3. f⃗=−2⋅a⃗\displaystyle \vec f = -2\cdot\vec a
    4. g⃗=a⃗−4b⃗+23c⃗\displaystyle \vec g = \vec a - 4\vec b + \frac{2}{3}\vec c
  2. 2

    Berechne den Lösungsvektor.

    1. (11)+2⋅(1−2)+(06)\displaystyle \begin{pmatrix}1\\1\end{pmatrix}+2\cdot\begin{pmatrix}1\\-2\end{pmatrix}+\begin{pmatrix}0\\6\end{pmatrix}

    2. 4⋅(0−2)+(60)−(03)4\cdot\begin{pmatrix}0\\-2\end{pmatrix}+\begin{pmatrix}6\\0\end{pmatrix}-\begin{pmatrix}0\\3\end{pmatrix}

    3. 5⋅(−33)−3⋅(−92)+4⋅(−3−2,25)5\cdot\begin{pmatrix}-3\\3\end{pmatrix}-3\cdot\begin{pmatrix}-9\\2\end{pmatrix}+4\cdot\begin{pmatrix}-3\\-2{,}25\end{pmatrix}

  3. 3

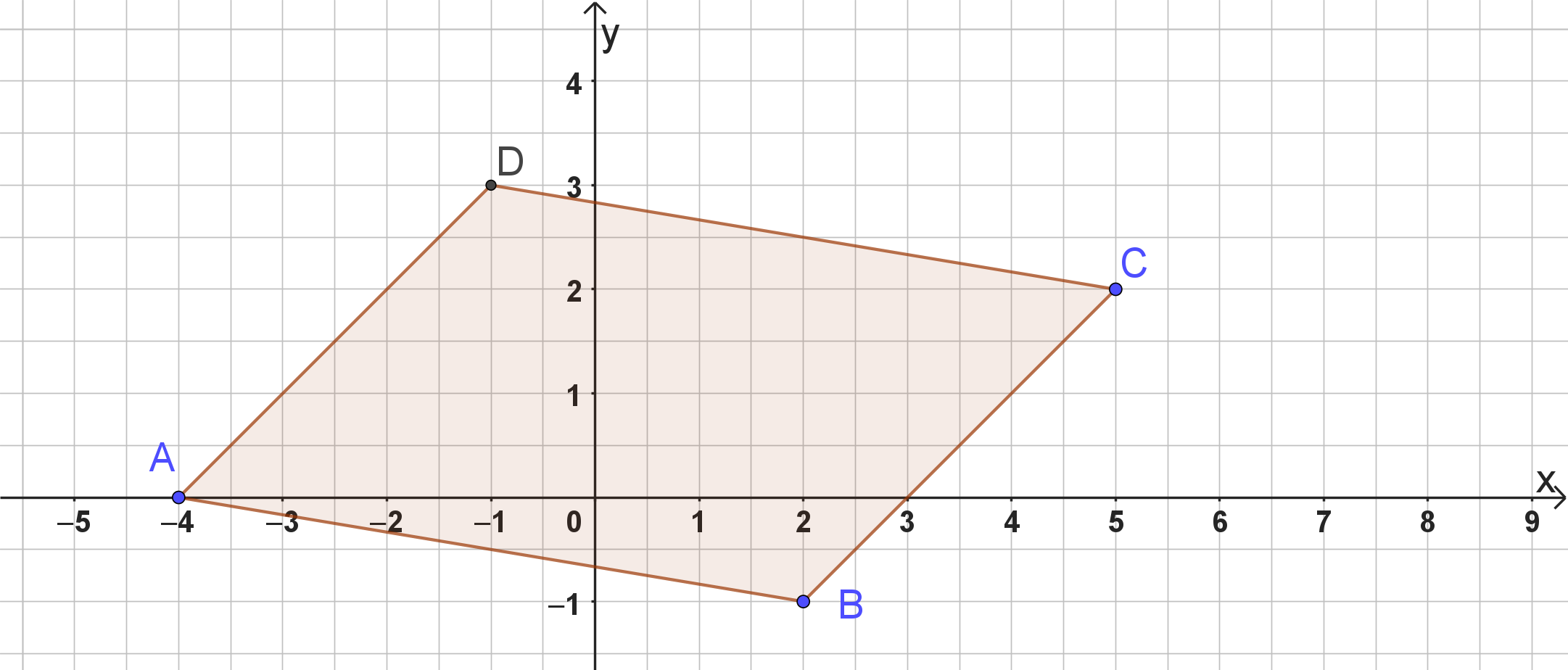
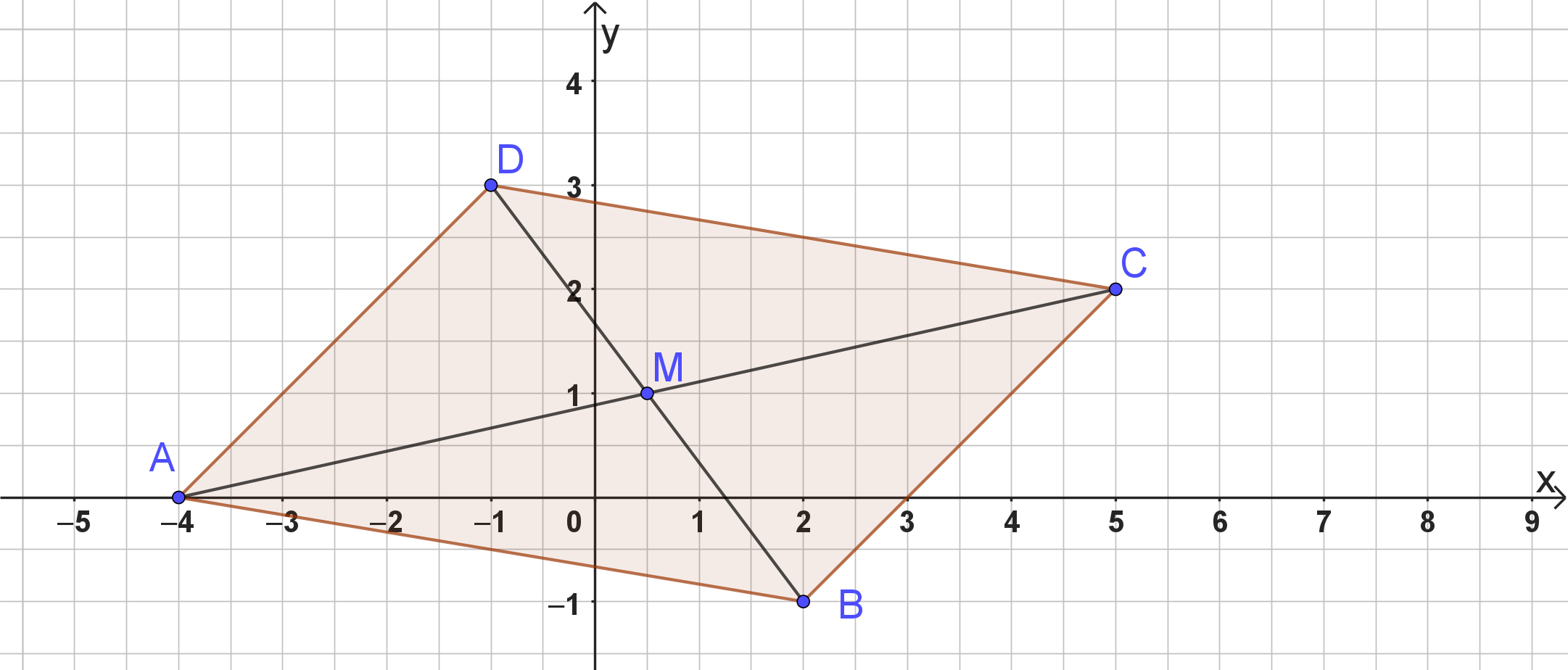
    Gegeben seien die Punkte A(−4∣0)A(-4|0), B(2∣−1)B(2|-1) und C(5∣2)C(5|2). Vervollständige zu einem Parallelogramm ABCD und berechne neben den Koordinaten von D auch die Lage des Schnittpunktes M seiner Diagonalen.

  4. 4

    Gegeben sind die Vektoren a⃗=(−12)\vec a=\begin{pmatrix} -1\\2\end{pmatrix} , b⃗=(34,5)\vec b=\begin{pmatrix}3\\4{,}5 \end{pmatrix} und c⃗=(50)\vec c=\begin{pmatrix}5\\0 \end{pmatrix}. Berechne jeweils den Vektor, der sich durch die angegebene Vektorkette ergibt!

    1. d⃗=7a⃗+2b⃗−25c⃗\displaystyle \vec d=7\vec a+2\vec b-\frac{2}{5}\vec c
    2. e⃗=23b⃗−4a⃗\displaystyle \vec e=\frac{2}{3}\vec b-4\vec a

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?