Nachtermin Teil B

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Das Rechteck $A B C D$ ist die Grundfläche des Quaders $A B C D E F G H$ . Der Punkt $E$ liegt senkrecht über dem Punkt $A$ .
Es gilt: $\overline{AB}=7{,}5 \text{cm}; \overline{BC}=10 \text{cm}; \overline{AE}=13 \text{cm}$
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
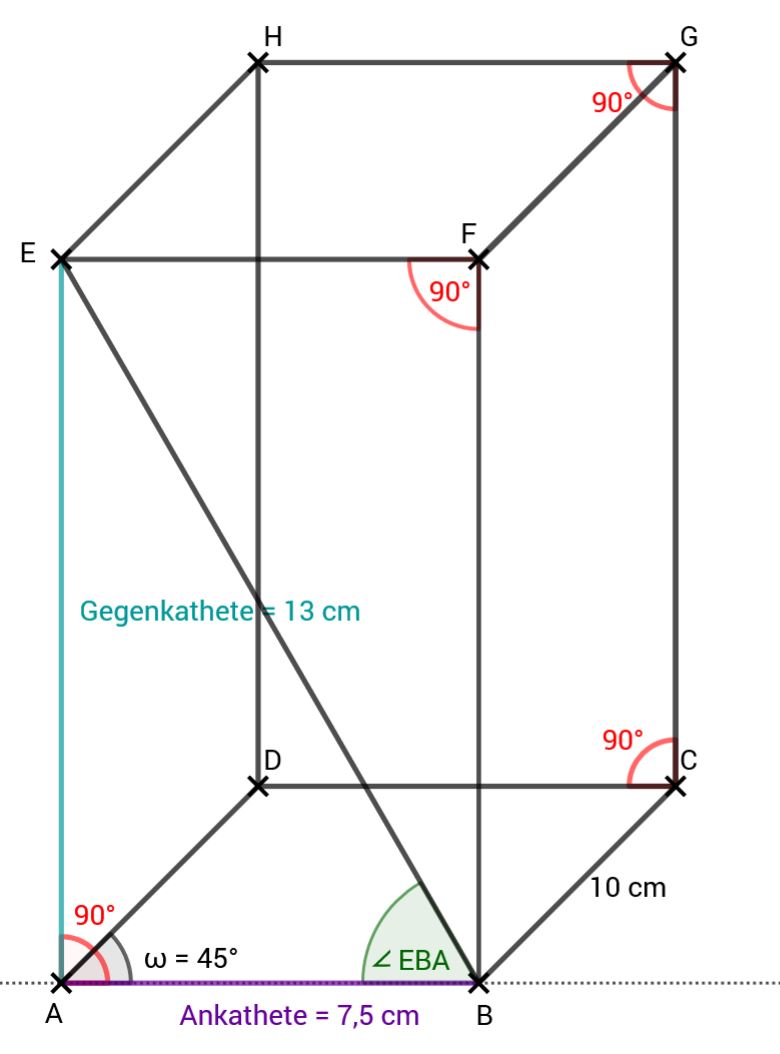
1. Zeichnen Sie das Schrägbild des Quaders $A B C D E F G H$ , wobei die Strecke $[A B]$ auf der Schrägbildachse und $A$ links von $B$ liegen soll.
  Für die Zeichnung gilt: $q=0{,}5;\ \omega=45\degree$ .
  Berechnen Sie sodann das Maß des Winkels $E B A$ .
  [Ergebnis: $\sphericalangle EBA = 60{,}02 \degree$ ]
  
  Schrägbild des Quaders
  In dieser Teilaufgabe ist das Schrägbild des Quaders $A B C D E F G H$ gesucht.
  Zunächst musst du wissen, was die Schrägbildachse ist und wie sie verläuft. Strecken entlang der Schrägbildachse bzw. Bildebene werden in wahrer Länge gezeichnet. Im folgenden kannst du dir die einzelnen Schritte anschauen, indem du auf den "weiter"-Button klickst.
  Berechnung des Winkels $\sphericalangle EBA$
  Den Winkel $\sphericalangle EBA$ kannst du mithilfe von Sinus, Kosinus und Tangens berechnen.
  In deiner Formelsammlung unter der Überschrift "Sinus, Kosinus und Tangens am rechtwinkligen Dreieck" findest du folgende Gleichung.
  $\tan\;\varphi\;=\;\frac {\text{y}}{\text{x}}\;=\;\frac{\text{Länge}\;\text{der}\;\text{Gegenkathete}}{\text{Länge}\;\text{der}\;\text{Ankathete}}$
  Daraus folgt:
  $\displaystyle \def\arraystretch{1.25} \begin{array}{rcl}\tan\sphericalangle EBA&=&\frac{13cm}{7{,}5cm}\\ \sphericalangle EBA&\approx&60{,}02^\circ \end{array}$
  Das Winkelmaß des Winkels $\sphericalangle EBA$ beträgt $60{,}02^\circ$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Punkte $P_{n}$ liegen auf der Strecke $[B E]$ . Die Winkel $B A P_{n}$ haben das Maß $\varphi$ mit $\varphi \in ]0 \degree; 90 \degree]$ .
  Die Punkte $P_{n}$ sind die Spitzen von Pyramiden $A B C D P_{n}$ mit der Grundfläche $A B C D$ und den Höhen $[P_{n} T_{n}]$ .
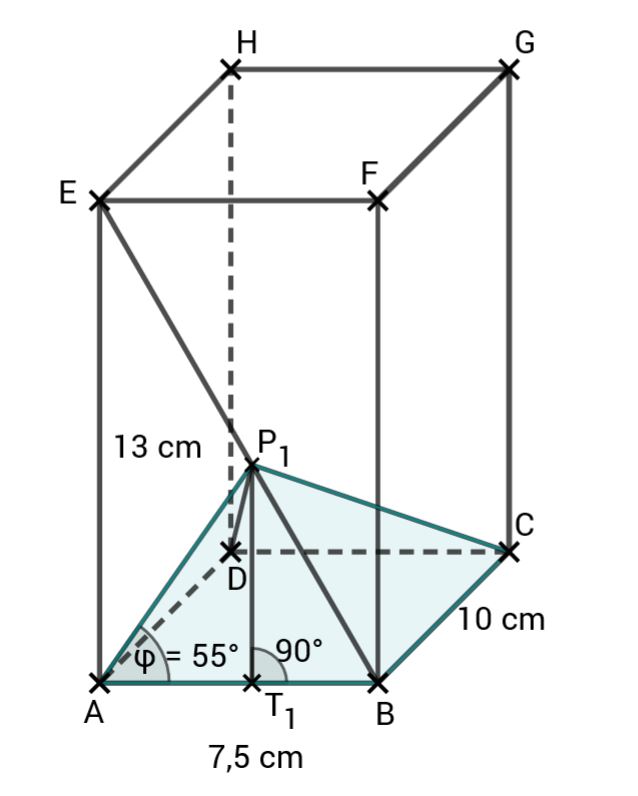
  Zeichnen Sie die Strecke $[B E]$ sowie die Pyramide $A B C D P_{1}$ für $\varphi=55 \degree$ und ihre Höhe $[P_{1} T_{1}]$ in die Zeichnung zu a.) ein.
  
  Gegeben ist, dass die Punkte $P_{n}$ auf der Strecke $[\text{BE}]$ liegen. Außerdem soll in der Zeichnung der Winkel $\varphi\;=\sphericalangle BAP_n=\:55^\circ$ sein. Der Punkt $P_{n}$ liegt in der Fläche $\text{EBA}$ und somit in der Fläche der Vorderseite des Quaders. Nun zeichnest du die Strecke $[B E]$ und die Höhe $[P_{1} T_{1}]$ ein.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Zeigen Sie durch Rechnung, dass für das Volumen $V$ der Pyramiden $A B C D P_{n}$ in Abhängigkeit von $\varphi$ gilt:
  $\displaystyle V(\varphi)=\frac{162{,}50\cdot\sin\varphi}{\sin(\varphi+60{,}02\degree)}\text{cm}_{ }^3$
  [Teilergebnis: $\overline{AP_n}(\varphi) = \frac{6{,}5}{\sin (\varphi + 60{,}02 \degree)}\text{cm}^3$ ]
  
  Gesucht ist das Volumen der Pyramide $A B C D P_{n}$ .
  Das Volumen einer Pyramide wird allgemein berechnet durch $\text{V}=\frac13\cdot\text{G}\cdot\text{h}$ .
  1) Bestimmen der Grundfläche der Pyramide $A B C D P_{n}$
  Die Grundfläche $G$ der Pyramide $A B C D P_{n}$ ist das Rechteck $A B C D$ . Den Flächeninhalt dieses Rechtecks berechnest du durch Länge mal Breite:
  $G=A_\text{ABCD}=\overline{AB}\cdot\overline{BC}=7{,}5\;\text{cm}\cdot10\;\text{cm} =75\;\text{cm}^2$
  Die Grundfläche der Pyramide $A B C D P_{n}$ beträgt also $75\;\text{cm}^2$ .
  2) Bestimmen der Höhe der Pyramide $A B C D P_{n}$
  Die Höhe $h$ der Pyramide $A B C D P_{n}$ ist die Strecke $[\text{P}_\text{n}\text{T}_\text{n}]$ mit der Länge $\overline{P_nT_n}(\varphi)$ . Diese berechnest du mithilfe von Sinus, Kosinus und Tangens im rechtwinkligen Dreieck:
  $\sin (\varphi )=\frac{\text{Gegenkathete}}{\text{Hypotenuse}}$
  $\sin (\varphi )=\frac{\overline{P_nT_n}(\varphi )}{\overline{AP_n}(\varphi )}$
  $\overline{P_nT_n}(\varphi)=\sin(\varphi)\cdot\overline{AP_n}(\varphi)$
  Nun berechnest du ${\overline{AP_n}}(\varphi)$ in Abhängigkeit von $\varphi$ mithilfe des Sinussatzes:
  $\def\arraystretch{1.25} \begin{array}{rcl} \displaystyle\frac{\overline{AP_n}(\varphi)}{\sin\sphericalangle P_nBA} &=& \displaystyle\frac{\overline{AB}}{\sin({180°-(\varphi+\sphericalangle}{{ P}_n}{B}{A}))}\\ \displaystyle\frac{\overline{AP_n}(\varphi)}{\sin\sphericalangle P_nBA} &=& \displaystyle\frac{\overline{AB}}{\underbrace{\sin({\varphi+\sphericalangle}{P_nBA})}_{Supplementbeziehung}}\\ \displaystyle\overline{AP_n}(\varphi) &=& \displaystyle\frac{\overline{AB}\cdot{\sin\sphericalangle P_nBA}}{\sin({\varphi+\sphericalangle}{P_nBA})}\\ \displaystyle\overline{AP_n}(\varphi) &=& \displaystyle\frac{7{,}5\cdot{\sin 60{,}02°}}{\sin({\varphi+60{,}02°})}\\ \displaystyle\overline{AP_n}(\varphi) &=& \displaystyle\frac{6{,}50}{\sin({\varphi+60{,}02°})}\text{cm} \end{array}$
  Daraufhin setzt du $\overline{AP_n}(\varphi)$ in die Gleichung für $\overline{{P_nT}_n}(\varphi)$ ein:
  $\def\arraystretch{1.25} \begin{array}{rcl} \overline{P_nT_n}(\varphi)&=&\sin(\varphi)\cdot{\overline{AP_n}}(\varphi)\\ &=&\displaystyle\sin(\varphi)\cdot\frac{6{,}50}{\sin({\varphi+60{,}02°})}\\ \overline{P_nT_n}(\varphi)&=&\displaystyle\frac{6{,}50\cdot\sin(\varphi)}{\sin({\varphi+60{,}02°})}\text{cm} \end{array}$
  3) Einsetzen in die Volumenformel
  Damit erhältst du für das Volumen $V(\varphi)$ der Pyramide $A B C D P_{n}$ :
  $\def\arraystretch{1.25} \begin{array}{rcl} V(\varphi) &=& \displaystyle\frac13\cdot A_{ABCD}\cdot\overline{P_nT_n}(\varphi)\\ V(\varphi) &=& \displaystyle\left[\frac{1}{3}\cdot 75\cdot \frac {6{,}50\cdot\sin(\varphi)} {\sin({\varphi+60{,}02°})} \right]\text{cm}^\text{3}\\ V(\varphi)&=& \displaystyle\left[\frac{162{,}5\cdot\sin(\varphi)}{\sin({\varphi+60{,}02°})} \right]\text{cm}^\text{3} \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Das gleichschenklige Dreieck $A D P_{2}$ hat die Basis $[D P_{2}]$ .
  Berechnen Sie den prozentualen Anteil des Volumens der Pyramide $A B C D P_{2}$ am Volumen des Quaders $A B C D E F G H$ .
  
  Der Quader $A B C D E F G H$ besitzt das Volumen
  $\displaystyle V_{Quader}=(7{,}5 \cdot 10 \cdot 13)=975 \text{ cm}^3.$
  Da die Strecke $\overline{AD}=10 \text{ cm}$ lang ist, muss auch $\overline{AP_2}=10 \text{ cm}$ sein.
  Du setzt einfach in die Gleichung von B2.3 ein:
  $\def\arraystretch{1.25} \begin{array}{rcl} \displaystyle\overline{AP_n}(\varphi) &=& \displaystyle\frac{6{,}50}{\sin({\varphi+60{,}02°})}\\ 10 &=& \displaystyle\frac{6{,}50}{\sin({\varphi+60{,}02°})}\\ \sin({\varphi+60{,}02°}) &=& \displaystyle\frac{6{,}50}{10}\\ \varphi_1+60{,}02°\approx 40{,}54°&\wedge&\varphi_2 +60{,}02°\approx 139{,}46°\\ \varphi_1=-19{,}48°&\wedge&\varphi_2=79{,}44° \end{array}$
  Da $\varphi \in ]0°;90°]$ , muss der gesuchte Winkel $\varphi=79{,}44°$ sein.
  Setze nun $\varphi=79{,}44°$ in die Volumenformel der Pyramide aus Aufgabe B2.3 ein:
  $\def\arraystretch{1.25} \begin{array}{rcl} V(79{,}44°)&=& \displaystyle\left[\frac{162{,}5\cdot\sin(79{,}44°)}{\sin({79{,}44°+60{,}02°})} \right]\text{cm}^\text{3}\\ V(79{,}44°)&\approx& 245{,}77\text{ cm}^\text{3} \end{array}$
  Nun musst du nur noch den prozentualen Anteil der Volumens der "kleinen" Pyramide am Volumen des "großen" Quaders angeben:
  $\displaystyle p=\frac{V_{Pyramide}}{V_{Quader}}=\frac{245{,}77}{975} \approx 0{,}2521 = 25{,}21\%$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Unter den Strecken $[A P_{n}]$ hat die Strecke $[A P_{3}]$ die minimale Länge.
  Bestimmen Sie das zugehörige Winkelmaß $\varphi$ sowie die Länge der Strecke $[A P_{3}]$ .
  Zeichnen Sie sodann die Strecke $[A P_{3}]$ in das Schrägbild zu A.) ein.
  
  Wenn die Länge der Strecke $[P_{3} T_{3}]$ minimal sein soll, muss es sich bei $[P_{3} T_{3}]$ um das Lot von $A$ auf die Strecke $[B E]$ handeln.
  Da der Winkel $\sphericalangle EBA$ das Maß $60,02$ ° besitzt und es sich beim Dreieck $A B P_{3}$ um ein rechtwinkliges Dreieck handelt, muss für $\sphericalangle BAP_3=\varphi_3$ gelten:
  $\displaystyle \sphericalangle BAP_3= 180°-(90°+60{,}02°)=29{,}98°$
  Mithilfe von Sinus, Kosinus und Tangens im rechtwinkligen Dreieck ergibt sich dann für die Länge $\overline{AP_3}$ :
  $\def\arraystretch{1.25} \begin{array}{rcl} \displaystyle \frac{\overline{AP_3}}{\overline{AB}}&=&\sin \sphericalangle EBA \\ \\ \displaystyle \overline{AP_3}&=&\overline{AB} \cdot \sin \sphericalangle EBA \\ \overline{AP_3}&=&7{,}5 \cdot \sin 60{,}02° \\ \overline{AP_3}&\approx&6{,}50 \text { cm} \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. Begründen Sie, dass für das Volumen der Pyramiden $A B C D P_{n}$ gilt:
  $V_{ABCDP_n}\le \frac{1}{3}\cdot V_{ABCDEFGH}$
  
  Zunächst überlegst du, wann die Pyramide $A B C D P_{n}$ das maximale Volumen besitzt:
  Eine Veränderung von $\varphi$ ändert nur $P_{n}$ und damit nur die Höhe der Pyramide, die Grundfläche bleibt dabei immer gleich.
  Daher kannst du sagen, die Pyramide $A B C D P_{n}$ hat ihr maximales Volumen bei $\varphi =90°$ .
  In diesem Fall ist $\overline{P_nT_n}=\overline{AE}$ , und damit gilt
  $\displaystyle V_{ABCDP_n}=\frac{1}{3}\cdot V_{ABCDEFGH}.$
  Probiere es selbst am Applet aus!
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Der Punkt $A (- 2 ∣ 0,5)$ ist gemeinsamer Eckpunkt von Rauten $A B_{n} C_{n} D_{n}$ . Die Eckpunkte $B_n(x|-1{,}5x+1{,}5)$ der Rauten $A B_{n} C_{n} D_{n}$ liegen auf der Geraden $g$ mit der Gleichung $y = - 1,5 x + 1,5$ mit $\mathbb{G}=\mathbb{R}\times\mathbb{R}$ .
Es gilt: $\sphericalangle B_nAD_n=60^\circ$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1. Zeichnen Sie die Gerade $g$ sowie die Rauten $A B_{1} C_{1} D_{1}$ für $x = - 0,5$ und $A B_{2} C_{2} D_{2}$ für $x = 2$ in ein Koordinatensystem.
  Für die Zeichnung: Längeneinheit $1 ~\text{cm};~-4\le x\le 7;~-2\le y\le 5$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
  Lösung zu a
  Die Zeichnung enthält bereits alle in der Aufgabe zu machenden Schritte.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ermitteln Sie rechnerisch die Koordinaten der Punkte $D_{n}$ in Abhängigkeit von der Abszisse der Punkte $B_{n}$ .
  $[$ Ergebnis: $D_n(1{,}80x-1{,}87|0{,}12x+2{,}73)]$
  
  Lösung zu b
  Die Koordinaten des Vektors $\overrightarrow{AD_n}$ erhältst du, indem du den Vektor $\overrightarrow{AB_n}$ um $A$ drehst, mit dem Drehwinkel $\varphi=60°$ (siehe Zeichnung).
  Für den Vektor $\overrightarrow{AB_n}$ erhältst du:
  $\overrightarrow{AB_n}=\overrightarrow{B_n}-\vec{A}=\begin{pmatrix}x\\-1{,}5x+1{,}5\end{pmatrix}-\begin{pmatrix}-2\\0{,}5\end{pmatrix}=\begin{pmatrix}x+2\\-1{,}5x+1\end{pmatrix}$
  Um dann die Koordinaten des Vektors $\overrightarrow{OD_n}$ (also des Punktes $D_{n}$ ) zu erhalten, musst du nach der Drehung den Vektor $\overrightarrow{OA}$ zu $\overrightarrow{AD_n}$ addieren (Vektorkette/Parallelverschiebung).
  Es ergibt sich also
  $\displaystyle \overrightarrow{OD_n}=\underbrace{\begin{pmatrix}\cos{60°}& -\sin{60°}\\\sin{60°} & \cos{60°}\end{pmatrix}\cdot\overrightarrow{AB_n}}_{\overrightarrow{AD_n}}+\overrightarrow{OA}$
  und weiter
  $\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} \overrightarrow{OD_n}&=&\begin{pmatrix}\frac12& -\frac{\sqrt 3}{2}\\\frac{\sqrt 3}{2} & \frac12\end{pmatrix}\cdot\begin{pmatrix}x+2\\-1{,}5x+1\end{pmatrix}+\begin{pmatrix}-2\\0{,}5\end{pmatrix}\\ &=& \begin{pmatrix}\frac12x+1+\frac{3\sqrt3}{4}x-\frac{\sqrt3}{2}\\ \frac{\sqrt3}{2}x+\sqrt3-\frac34x+\frac12\end{pmatrix}+\begin{pmatrix}-2\\0{,}5\end{pmatrix}\\ &=& \begin{pmatrix}\frac12x+1+\frac{3\sqrt3}{4}x-\frac{\sqrt3}{2}-2\\ \frac{\sqrt3}{2}x+\sqrt3-\frac34x+\frac12+\frac12\end{pmatrix}\\ \overrightarrow{OD_n}&=&\begin{pmatrix}1{,}80x-1{,}87\\0{,}12x+2{,}73\end{pmatrix}. \end{array}$
  Damit hat der Punkt $D_{n}$ die Koordinaten $D_n(1{,}80x-1{,}87|0{,}12x+2{,}73)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Bestimmen Sie die Gleichung des Trägergraphen $h$ der Punkte $D_{n}$ und zeichnen Sie sodann den Trägergraphen $h$ in das Koordinatensystem zur Teilaufgabe (a) ein.
  $[$ Ergebnis: $h : y = 0,07 x + 2,85]$
  
  Lösung zu c
  Wir nehmen an, die Koordinaten des Punktes $D_{n}$ lauten $D_{n} (x^{'} ∣ y^{'})$ , da der Punkt ja ein "eigenes" $x$ bekommen soll.
  Außerdem lauten die Koordinaten des Punktes $D_{n}$ auch
  $\displaystyle D_n(1{,}80x-1{,}87|0{,}12x+2{,}73)$
  in Abhängigkeit von $x_{B_n}$ (siehe Teilaufgabe (b)).
  Daraus ergibt sich nun folgende Gleichung:
  $\def\arraystretch{1.25} \begin{array}{rrcl} (I)&x'&=&1{,}80x-1{,}87 \Rightarrow x = \frac{x'+1{,}87}{1{,}80} \\ (II)& y'&=&0{,}12x+2{,}73\\ \\ (I') \text{ in } (II):& y'&=&0{,}12\cdot\left(\frac{x'+1{,}87}{1{,}80}\right)+2{,}73\\ & y'&=&\left(\frac{0{,}12\cdot x'+0{,}12\cdot1{,}87}{1{,}80}\right)+2{,}73\\ & y'&=&0{,}07x'+2{,}85\\ \\ h:&y&=&0{,}07x+2{,}85 \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Zeigen Sie, dass für den Umfang $u$ der Rauten $A B_{n} C_{n} D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ gilt: $u(x)=\sqrt{52x^2+16x+80}~\text{LE}$ .
  
  Lösung zu d
  Den Umfang einer Raute berechnest du, indem du die Länge einer Seite bestimmst und dann mit vier multiplizierst.
  Daher musst du bei dieser Aufgabe lediglich die Länge des Vektors $\overrightarrow{AB_n}$ in Abhängigkeit von $x$ bestimmen ( $\overrightarrow{AB_n}$ selbst wurde in Teilaufgabe (b) schon bestimmt).
  $\displaystyle \overrightarrow{AB_n}=\begin{pmatrix}x+2\\-1{,}5x+1\end{pmatrix}$
  $\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} u(x)&=&4\cdot \sqrt{(x+2)^2+(-1{,}5x+1)^2}~\text{LE}\\ &=&4\cdot \sqrt{x^2+4x+4+2{,}25x^2-3x+1}~\text{LE}\\ &=&4\cdot \sqrt{3{,}25x^2+x+5}~\text{LE}\\ &=&\sqrt{16\cdot(3{,}25x^2+x+5)}~\text{LE}\\ u(x)&=&\sqrt{52x^2+16x+80)}~\text{LE} \end{array}$
  Analog würde es über die Koordinaten der Punkte $A$ und $B_{n}$ , also der Länge der Strecke $\overline{AB_n}$ funktionieren.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. Der Punkt $B_{3}$ der Raute $A B_{3} C_{3} D_{3}$ liegt auf dem Trägergraphen $h$ der Punkte $D_{n}$ .
  Berechnen Sie den Umfang der Raute $A B_{3} C_{3} D_{3}$ .
  
  Lösung zu e
  Wenn der Punkt $B_{3}$ sowohl auf der Geraden $g$ liegen soll (wie jeder Punkt $B_{n}$ laut Angabe) und zugleich auf der Geraden $h$ , dann kann es sich beim Punkt $B_{3}$ nur um den Schnittpunkt dieser beiden Geraden handeln.
  Um das gemeinsame $x_{3}$ zu berechnen, musst du lediglich die beiden Geradengleichungen gleichsetzen:
  $\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} y_g&=&y_h\\ -1{,}5x+1{,}5&=&0{,}07x+2{,}85\\ -1{,}5x-0{,}07x&=&2{,}85-1{,}5\\ -1{,}57x&=&1{,}35\\ x_3&\approx&-0{,}86 \end{array}$
  Um nun den Umfang der Raute $A B_{3} C_{3} D_{3}$ in Abhängigkeit von $x$ zu bestimmen, setzt du $x_3=-0{,}86$ in die Gleichung für den Umfang (siehe Teilaufgabe (d)) ein:
  $\def\arraystretch{1.25} \begin{array}{rcl}u(x)&=&\sqrt{52x^2+16x+80)}~\text{LE}\\u(x)&=&\sqrt{52\cdot(-0{,}86)^2+16\cdot(-0{,}86)+80)}~\text{LE}\\u(x)&\approx&10{,}23~\text{LE}\end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. Die Diagonale $[B_{4} D_{4}]$ der Raute $A B_{4} C_{4} D_{4}$ ist parallel zur $y$ -Achse.
  Bestimmen Sie den zugehörigen Wert für $x$ und geben Sie den Flächeninhalt der Raute $A B_{4} C_{4} D_{4}$ an.
  
  Lösung zu f
  Wenn die Diagonale $[B_{4} D_{4}]$ parallel zur y-Achse sein soll, heißt das, dass die x-Koordinaten der beiden Punkte $B_{4}$ und $D_{4}$ gleich sein müssen.
  Du kannst also das gemeinsame $x_{4}$ berechnen, indem du die x-Koordinaten der Punkte $B_{n}$ und $D_{n}$ gleichsetzt:
  $\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} x&=&1{,}80x-1{,}87\\ -0{,}80x&=&-1{,}87\\ x&\approx&2{,}34 \end{array}$
  Setze $x = 2,34$ in $y_{B_n}=-1{,}5\cdot x+1{,}5$ ein:
  $y_{B_n}=-1{,}5\cdot 2{,}34+1{,}5=-2{,}01$
  Für $B_{4}$ ergibt sich also $B_4(2{,}34|-2{,}01)$ .
  Für die Berechnung des Flächeninhalts der so entstandenen Raute gibt es einige unterschiedliche Berechnungsmöglichkeiten.
  (Verwende geschickterweise die Berechnung, die am zeitsparendsten und am wenigsten fehleranfällig ist.)
  Wenn man die Raute $A B_{4} C_{4} D_{4}$ betrachtet fällt auf, dass die Diagonalen sich recht leicht berechnen lassen:
  die Diagonale $[A C_{4}]$ hat die doppelte Länge des Abstandes der x-Koordinaten von $A (- 2 ∣ 0,5)$ und $B_4(2{,}34|-2{,}01)$ :
  $\displaystyle \overline{AC_4}= 2\cdot (x_{B_4}-x_A)$
  die Diagonale $[B_{4} D_{4}]$ hat die Länge des Abstandes der y-Koordinaten von $B_{4}$ und $D_{4}$ :
  $\displaystyle \overline{B_4D_4}=(y_{D_4}-y_{B_4})=2\cdot (y_A-y_{B_4})$
  Nun kannst du mit der Flächenformel den Flächeninhalt der Raute berechnen:
  $\displaystyle A_{Raute}=\frac12 \cdot e\cdot f$
  wobei $e$ und $f$ die Diagonalen der Raute sind:
  $\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} A_{AB_4C_4D_4}&=&\frac12 \cdot 2\cdot (x_{B_4}-x_A)\cdot 2\cdot (y_A-y_{B_4})\\ &=&\frac12 \cdot 2\cdot (2{,}34+2)\cdot 2\cdot (0{,}5+2{,}01)\\ &\approx&21{,}79~\text{FE} \end{array}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Nachtermin Teil B

Schrägbild des Quaders

Berechnung des Winkels ∢EBA\sphericalangle EBA∢EBA

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

1) Bestimmen der Grundfläche der Pyramide ABCDPnABCDP_nABCDPn​

2) Bestimmen der Höhe der Pyramide ABCDPnABCDP_nABCDPn​

3) Einsetzen in die Volumenformel

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lösung zu a

Hast du eine Frage oder Feedback?

Lösung zu b

Hast du eine Frage oder Feedback?

Lösung zu c

Hast du eine Frage oder Feedback?

Lösung zu d

Hast du eine Frage oder Feedback?

Lösung zu e

Hast du eine Frage oder Feedback?

Lösung zu f

Hast du eine Frage oder Feedback?

Berechnung des Winkels $\sphericalangle EBA$

1) Bestimmen der Grundfläche der Pyramide $A B C D P_{n}$

2) Bestimmen der Höhe der Pyramide $A B C D P_{n}$