Rechen- und Verständnisaufgaben zur Quadratwurzel

1

Die großen Flächen eines Zauberwürfels bestehen aus $9$ kleinen bunten Flächen. Insgesamt hat der Würfel einen Oberflächeninhalt von $900\,\mathrm{cm}^2$ .

Wie groß sind die Flächen der einzelnen Farbquadrate?

cm²

2

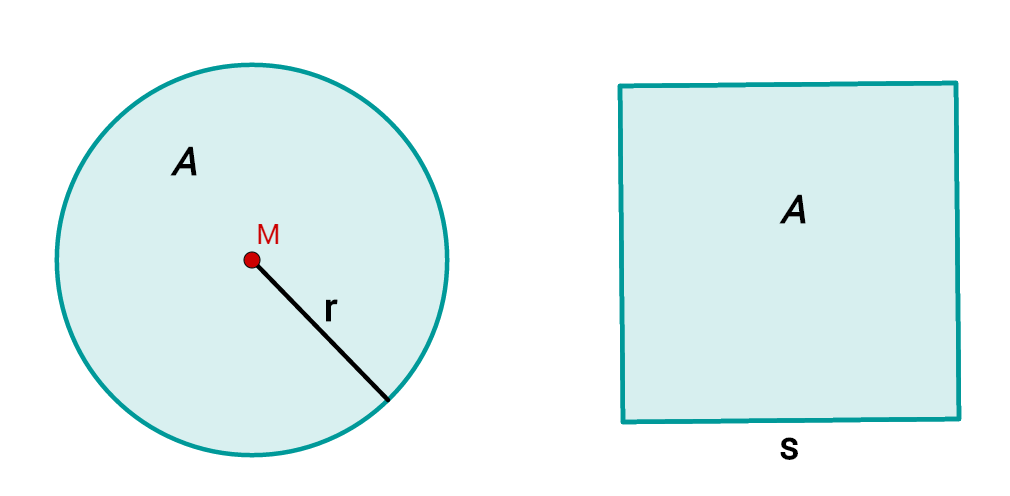
Ein Quadrat und ein Kreis haben denselben Flächeninhalt.

Der Radius vom Kreis beträgt $13{,}6 \,\mathrm{cm}$ . Wie groß ist die Seitenlänge des Quadrats?

cm

3

Welche Terme sind definiert?

$\sqrt{25}$
$\sqrt{7-3}$
$\sqrt{-25}$
$\sqrt{5-7}$

4

Welche Terme sind definiert?

$5^\frac{1}{2}$
$\sqrt{2}$
$\sqrt{-3}$
$(-5)^\frac{1}{2}$

5

Schätze den Wert von $\sqrt{7}$ .

Berechne dazu die ersten fünf Schritte der Intervallschachtelung und schätze anschließend den Wert von $\sqrt{7}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Intervallschachtelung

Die Methode der Intervallschachtelung ist eine Möglichkeit der Abschätzung von Werten von Wurzeln.

Überlege dir für den ersten Schritt ein Intervall, in dem der Wert von $\sqrt{7}$ liegen kann. Nutze dazu bereits bekannte Wurzelwerte.

1. Schritt

Du kennst bereits die Werte von:

$\sqrt{4}$ und $\sqrt{9}$

Daraus kannst du die erste Abschätzung machen:

$\def\arraystretch{1.25} \begin{array}{} 2^2 &< &7 &< &3^2\\4 &<&7 &<&9\end{array}$

daraus folgt wiederum:

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Das bedeutet, der Wert von $\sqrt{7}$ liegt im Intervall:

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Die nächsten Schritte laufen immer in der gleichen Reihenfolge ab. Du bildest zuerst den Mittelwert der alten Intervallgrenzen. Dieser Wert bildet wiederum eine der neuen Intervallgrenzen. Die andere bleibt erhalten.

Ob der neue Wert die obere oder untere Intervallgrenze ist, entscheidest du wie folgt: quadriere den Mittelwert und vergleiche diesen Wert mit der $7$ .

Wenn er

größer als $7$ ist, bildet er die neue Obergrenze
kleiner als $7$ ist, bildet er die neue Untergrenze

Eine ausführliche Erklärung dieser Schritte findest du hier.

2. Schritt

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Bilde den Mittelwert der Intervallgrenzen von $I_0$ !

$\dfrac{2+3}{2}=2{,}5$

Berechne das Quadrat von $2{,}5$ und vergleiche es mit $7$ .

$2{,}5^2 = 6{,}25$

$6{,}25 < 7 < 9$

$2{,}5^2 < 7 <3^2$

Definiere nun das neue Intervall!

$I_1 = \left]2{,}5\; ; \; 3\right[$

3. Schritt

$I_1 = \left]2{,}5\; ; \; 3\right[$

Bilde den Mittelwert der Intervallgrenzen von $I_1$ !

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Berechne das Quadrat des Mittelwertes und vergleiche es mit $7$ .

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

$\def\arraystretch{1.25} \begin{array}{cccc}\ 6{,}25 &< &7 &< &7{,}56 \\2{,}5^2 &< &7 &< &2{,}75^2\end{array}$

Definiere nun das neue Intervall!

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

4. Schritt

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Bilde den Mittelwert der Intervallgrenzen von $I_2$ !

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Berechne das Quadrat von $2{,}625$ und vergleiche es mit $7$ .

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

$\def\arraystretch{1.25} \begin{array}{ccc}\ 6{,}89 &< &7 &< &7{,}56\\2{,}625^2 &< &7 &< &2{,}75^2\end{array}$

Definiere nun das neue Intervall!

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

5. Schritt

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Bilde den Mittelwert der Intervallgrenzen von $I_2$ !

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Berechne das Quadrat des Mittelwerts und vergleiche mit $7$ .

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Definiere nun das neue Intervall!

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Nach diesen fünf Schritten wissen wir:

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Also: Der Wert von $\sqrt{7}$ liegt zwischen $2{,}625$ und $2{,}6875$ .

Abschätzung

Nimm den Mittelwert der letzten Intervallgrenzen als mögliche Abschätzung für den Wert von $\sqrt{7}$ .

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Die Abschätzung von $\sqrt{7}$ ergibt $2{,}65625$ .

Als Vergleich: Der Taschenrechner rundet auf $2{,}64575$ .

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

6

Schätze den Wert von $\sqrt{7}$ .

Berechne dazu die ersten vier Schritte des Heron-Verfahrens und schätze anschließend den Wert von $\sqrt{7}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Heron-Verfahren

Heron-Verfahren

Das Heron-Verfahren ist eine Methode, um den Wert von Wurzeln (schrittweise) abzuschätzen.

Du suchst ein Quadrat, dessen Flächeninhalt genau dem Radikanden $7$ entspricht. Dazu bildest du zuerst ein Rechteck, dessen Seiten du Schritt für Schritt veränderst.

1. Schritt

Das erste Rechteck findest du, indem du einen Teiler des Radikanden suchst und dann die zweite Seite durch Auflösen der Formel für den Flächeninhalt für Rechtecke.

$A=a\cdot b$

$A$ entspricht dem Radikanden. In unserem Fall ist $A=7$ und nur durch $1$ und sich selbst $7$ teilbar. Daraus ergeben sich unsere Anfangswerte $a_0$ und $b_0$ .

$a_0=7$

$b_0=1$

Im Bild unten siehst du das anfängliche Rechteck.

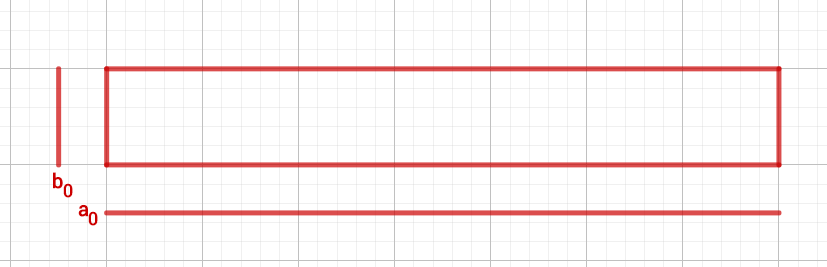
Die nächsten Schritte laufen immer in der folgenden Reihenfolge ab:

Zuerst bildest du den Mittelwert der alten Werte und berechnest daraus dein neues $a$ .
$b$ findest du, indem du $b = \frac{A}{a}$ rechnest und dort das neue $a$ einsetzt und den Radikanden für $A$ .

Eine ausführliche Erklärung dieser Schritte findest du hier.

2. Schritt

Bilde den Mittelwert von $a_0$ und $b_0$ .

$a_1 = \dfrac{a_0+b_0}{2} = \dfrac{7+1}{2}=4$

Berechne anschließend $b_1$ .

$b_1 = \dfrac{A}{a_1} = \dfrac{\text{Radikand}}{a_1} = \dfrac{7}{4} = 1{,}75$

Deine neuen Werte:

$a_1=4$

$b_1=1{,}75$

Im Bild unten siehst du das ursprüngliche Rechteck und das neue, das sich mehr einem Quadrat angenähert hat.

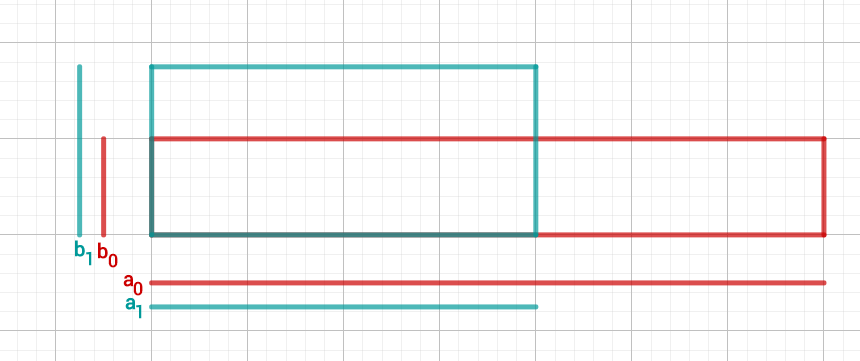
3. Schritt

Bilde den Mittelwert von $a_1$ und $b_1$ .

$a_2 = \dfrac{a_1+b_1}{2} = \dfrac{4+1{,}75}{2}=2{,}875$

Berechne anschließend $b_2$ .

$b_2 = \dfrac{A}{a_2} = \dfrac{\text{Radikand}}{a_2}\\ \; \; \; = \dfrac{7}{2{,}875} = 2{,}4348$

Deine neuen Werte sind:

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Im Bild unten siehst du die Veränderung der Rechtecke.

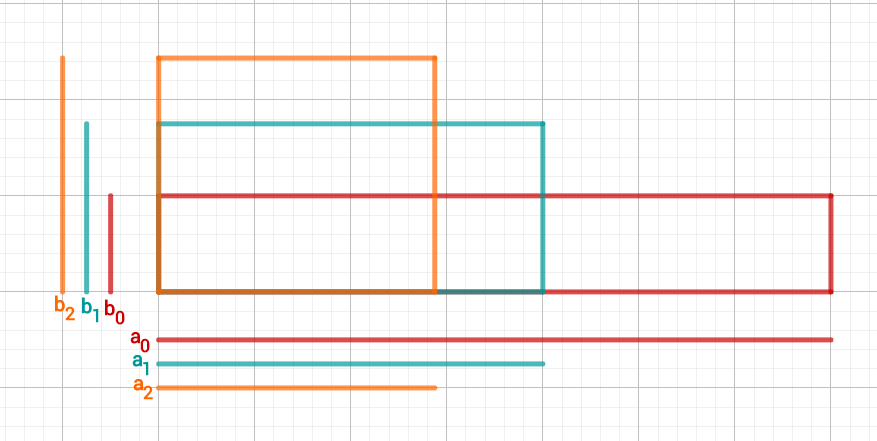
4. Schritt

Bilde den Mittelwert von $a_2$ und $b_2$ .

$a_3 = \dfrac{a_2+b_2}{2} = \dfrac{2{,}875+2{,}4348}{2}=2{,}6548$

Berechne nun $b_3$ .

$b_3 = \dfrac{A}{a_3} = \dfrac{\text{Radikand}}{a_3}\\ \; \; \; = \dfrac{7}{2{,}6548} = 2{,}6367$

Deine endgültigen Werte sind $a_3=2{,}6548$ und $b_3=2{,}6367$ .

Wie dir auffällt, haben sich die beiden Werte sehr stark angenähert.

Im Bild unten siehst du die Veränderung der Rechtecke. Das letzte (lila) ist schon nah an einem Quadrat.

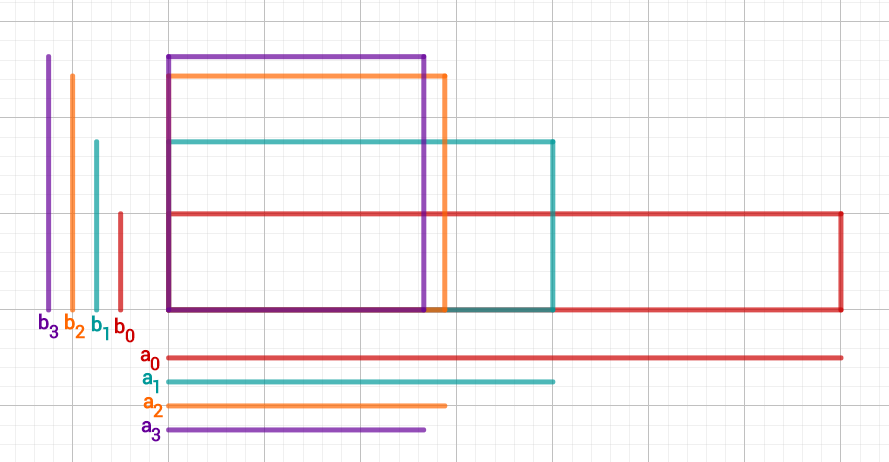
Abschätzung

Für die Abschätzung bildest du nochmal den Mittelwert zwischen den beiden letzten Seiten.

\displaystyle \sqrt{4}<\sqrt{7}<\sqrt{9}

Zum Vergleich: Wenn du den Wert im Taschenrechner berechnest, erhältst du den gerundeten Wert: $2{,}64575$ .

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

7

Ziehe die Wurzel soweit wie möglich:

$\sqrt{20}$

$\sqrt{27}$

$\sqrt{45}$

$\sqrt{98}$

$\sqrt{180}$

$\frac{\sqrt{ 8}}{2}$

$\displaystyle A_{Kreis}$	$=$	$\displaystyle \pi r^2$
	↓	Das ist der Flächeninhalt, den das Quadrat auch hat.
$\displaystyle A_{Kreis}$	$=$	$\displaystyle \pi\cdot\left(13{,}6cm\right)^2$
	$≈$	$\displaystyle 581{,}07\ cm^2$

$\displaystyle A_{Quadrat}$	$=$	$\displaystyle s^2$
	↓	Stelle diese nun nach der Seitenlänge $s$ um.
$\displaystyle A_{Quadrat}$	$=$	$\displaystyle s^2$	$\displaystyle \sqrt{ }$
	↓	Du erhältst zwei Lösungen
$\displaystyle \sqrt{A_{Quadrat}}$	$=$	$\displaystyle \pm s$
$\displaystyle \sqrt{581{,}07\ cm^2}$	$≈$	$\displaystyle \pm24{,}11\ cm$

$\displaystyle \sqrt{20}$	$=$
	↓	Mache die Primfaktorenzerlegung.
	$=$	$\displaystyle \sqrt{2\cdot2\cdot5}$
	↓	Suche gerade Exponenten in der Zerlegung.
	$=$	$\displaystyle \sqrt{2^2\cdot5}$
	↓	Zerlege die Wurzel.
	$=$	$\displaystyle \sqrt{2^2}\cdot\sqrt{5}$
	↓	Ziehe die Wurzel.
	$=$	$\displaystyle 2\cdot\sqrt{5}$
	$=$	$\displaystyle 2\sqrt{5}$

$\displaystyle \sqrt{27}$	$=$
	↓	Mache die Primfaktorenzerlegung.
	$=$	$\displaystyle \sqrt{3\cdot3\cdot3}$
	↓	Suche gerade Exponenten in der Zerlegung.
	$=$	$\displaystyle \sqrt{3^2\cdot3}$
	↓	Zerlege die Wurzel.
	$=$	$\displaystyle \sqrt{3^2}\cdot\sqrt{3}$
	↓	Ziehe die Wurzel.
	$=$	$\displaystyle 3\cdot\sqrt{3}$
	$=$	$\displaystyle 3\sqrt{3}$

$\displaystyle \sqrt{45}$	$=$
	↓	Mache die Primfaktorenzerlegung.
	$=$	$\displaystyle \sqrt{3\cdot3\cdot5}$
	↓	Suche gerade Exponenten in der Zerlegung.
	$=$	$\displaystyle \sqrt{3^2\cdot5}$
	↓	Zerlege die Wurzel.
	$=$	$\displaystyle \sqrt{3^{2\cdot5}}$
	↓	Ziehe die Wurzel.
	$=$	$\displaystyle 3\cdot\sqrt{5}$
	$=$	$\displaystyle 3\sqrt{5}$

Rechen- und Verständnisaufgaben zur Quadratwurzel

Berechnung des Flächeninhaltes von einem einzelnen Farbquadrat

Antwort:

Seitenlänge des Quadrats bestimmen

1. Schritt

2. Schritt

3. Schritt

4. Schritt

5. Schritt

Abschätzung

Heron-Verfahren

1. Schritt

2. Schritt

3. Schritt

4. Schritt

Abschätzung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

$\displaystyle \sqrt{98}$	$=$
	↓	Mache die Primfaktorenzerlegung.
	$=$	$\displaystyle \sqrt{2\cdot7\cdot7}$
	↓	Suche gerade Exponenten in der Zerlegung.
	$=$	$\displaystyle \sqrt{2\cdot7^2}$
	↓	Zerlege die Wurzel.
	$=$	$\displaystyle \sqrt{2}\cdot\sqrt{7^2}$
	↓	Ziehe die Wurzel.
	$=$	$\displaystyle \sqrt{2}\cdot7$
	$=$	$\displaystyle 7\sqrt{2}$

$\displaystyle \ \sqrt{180}$	$=$
	↓	Mache die Primfaktorenzerlegung.
	$=$	$\displaystyle \sqrt{2\cdot2\cdot3\cdot3\cdot5}$
	↓	Suche gerade Exponenten in der Zerlegung.
	$=$	$\displaystyle \sqrt{2^2\cdot3^2\cdot5}$
	↓	Zerlege die Wurzel.
	$=$	$\displaystyle \sqrt{2^2}\cdot\sqrt{3^2}\cdot\sqrt{5}$
	↓	Ziehe die Wurzel.
	$=$	$\displaystyle 2\cdot3\cdot\sqrt{5}$
	$=$	$\displaystyle 6\cdot\sqrt{5}$
	$=$	$\displaystyle 6\sqrt{5}$

$\displaystyle \frac{\sqrt{8}}{2}$	$=$
	↓	Mache die Primfaktorenzerlegung.
	$=$	$\displaystyle \frac{\sqrt{2\cdot2\cdot2}}{2}$
	↓	Suche gerade Exponenten in der Zerlegung.
	$=$	$\displaystyle \frac{\sqrt{2^2\cdot2}}{2}$
	↓	Zerlege die Wurzel.
	$=$	$\displaystyle \frac{\sqrt{2^2}\cdot\sqrt{2}}{2}$
	↓	Ziehe die Wurzel.
	$=$	$\displaystyle \frac{2\cdot\sqrt{2}}{2}$
	$=$	$\displaystyle \sqrt{2}$