Aufgaben zum Verschieben und Strecken trigonometrischer Funktionen

1
Finde die passenden Gleichungen zu den Funktionsgraphen:
1. Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus- und Kosinusfunktion
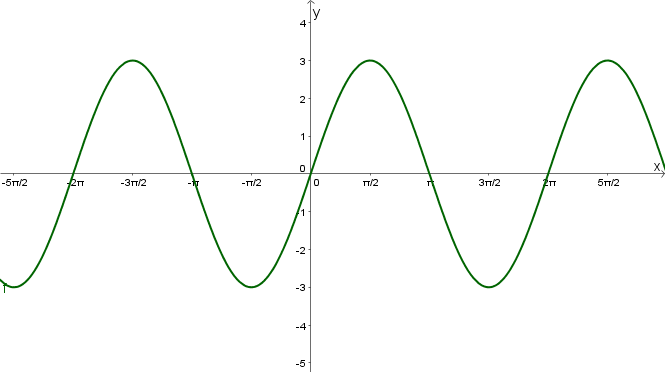
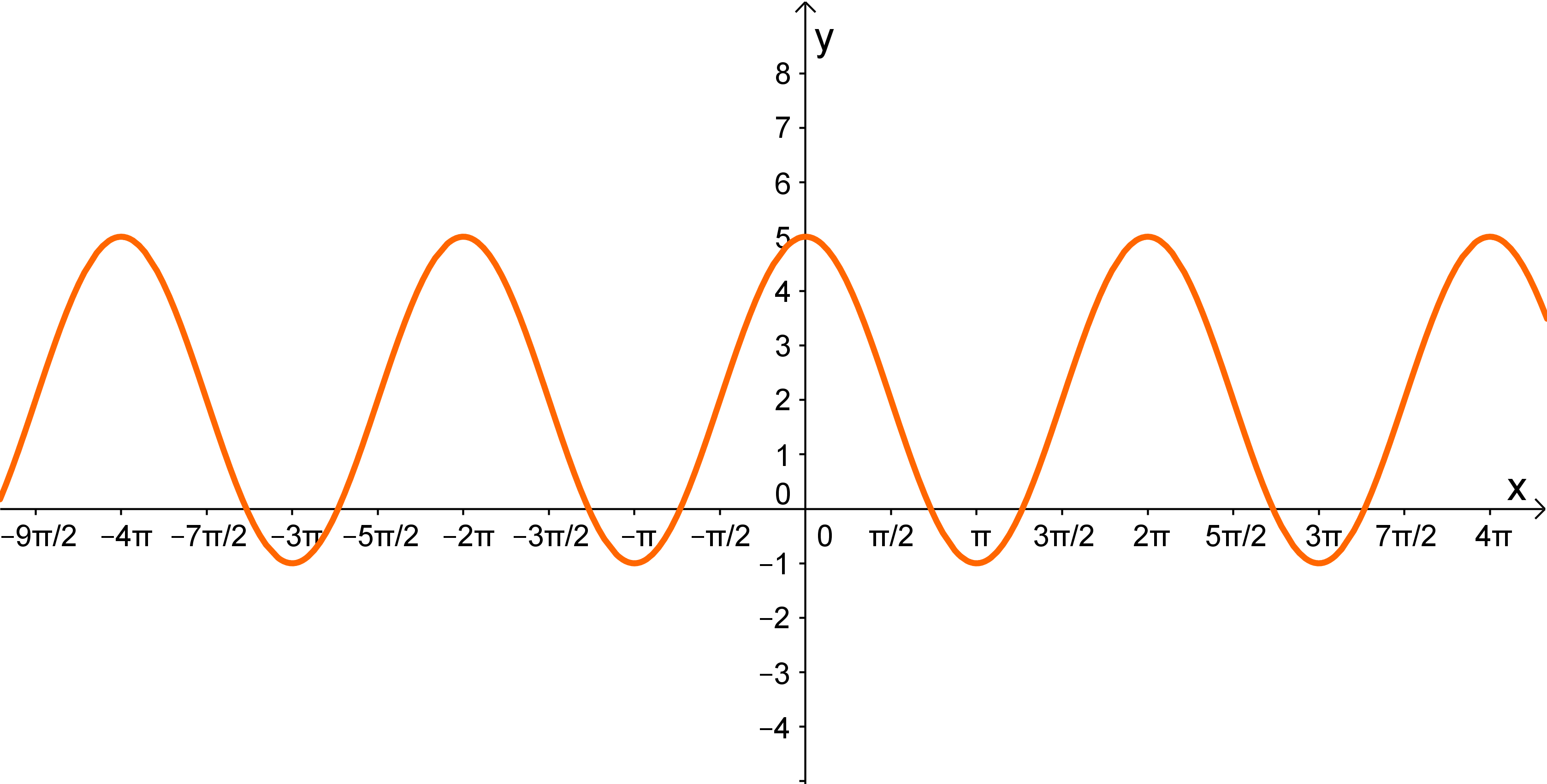
  Die Ruhelage der Funktion liegt auf der $x$ -Achse.
  Der Graph schneidet das Koordinatensystem im Nullpunkt, also handelt es sich um eine Sinusfunktion (beziehungsweise einen verschobenen Kosinus).
  Da es leichter ist, verwendest du in den weiteren Schritten die Sinusfunktion.
  Im nächsten Schritt suchst du nach der Amplitude der Funktion.
  Die Amplitude der Funktion ist $3$ . Das heißt, dass die Funktion vorerst von der Form $f(x)=3\cdot\sin(x)$ ist.
  Jetzt fehlt dir nur noch die Periode der Funktion. Am Graphen kannst du ablesen, dass diese $2\pi$ beträgt. Das ist die normale Periode von der Sinusfunktion.
  Da die Periode der Sinusfunktion nicht verändert wurde, lautet die Funktion:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
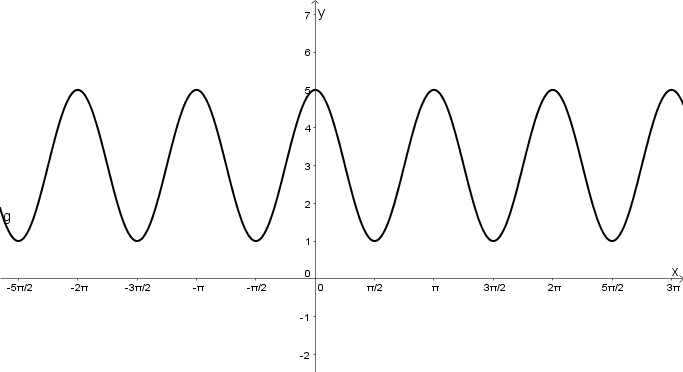
2. Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus- und Kosinusfunktion
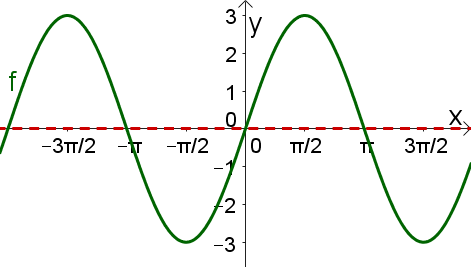
  Bestimme zunächst die Ruhelage der Funktion.
  Ruhelage bestimmen
  Die Ruhelage der Funktion liegt $3$ Einheiten über der $x$ -Achse.
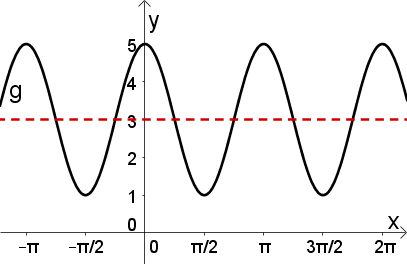
  Der Graph hat ein Extremum (E) auf der $y$ -Achse. Das heißt, es handelt sich um eine Kosinusfunktion (beziehungsweise eine verschobene Sinusfunktion).
  Da es leichter ist, beschränken wir uns hier auf die Kosinusfunktion.
  Aufgrund der bisherigen Erkenntnisse gehen wir zunächst von folgender Form aus:
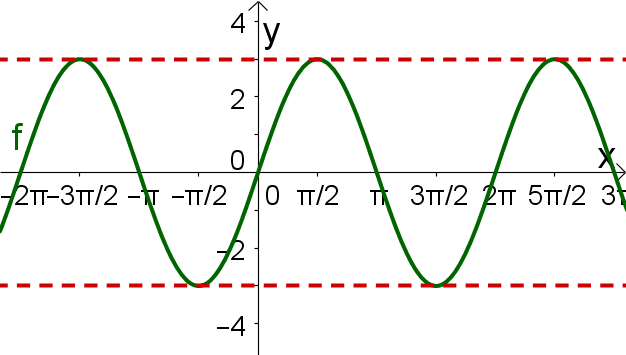
  Amplitude ermitteln
  Als nächsten Schritt betrachten wir die Amplitude der gegeben Kosinusfunktion. Dazu müssen wir den Abstand eines Extremums zu der Ruhelage herausfinden.
  Die Amplitude der Funktion hat den Wert $2$ . Das heißt, sie ist doppelt so groß wie bei der normalen Sinusfunktion. Daraus ergibt sich die vorläufige Form der Funktion:
  Untersuchung der Periode
  Als nächstes untersuchst du die Periode der Funktion. Dazu untersuchst du, wie viele Perioden der gegebenen Funktion in dem Intervall $[0{,}2\pi]$ liegen. Bei der normalen Kosinusfunktion liegt in diesem Intervall genau eine Periode. Hier sind es genau zwei Perioden, da im halben Intervall $[0,\pi]$ eine Periode liegt. Also ist die Funktion um den Faktor $2$ gestaucht.
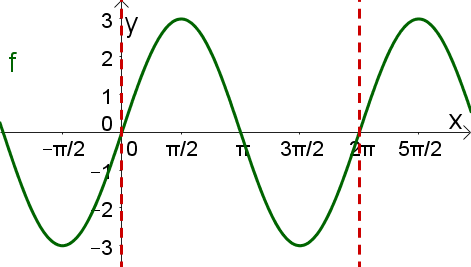
  Ergebnis
  Da die Funktion um den Faktor $2$ gestaucht ist, lautet die Funktion:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
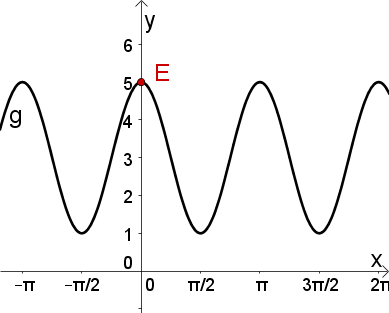
3. Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus- und Kosinusfunktion
  Die Ruhelage der Funktion liegt bei $y=2$ .
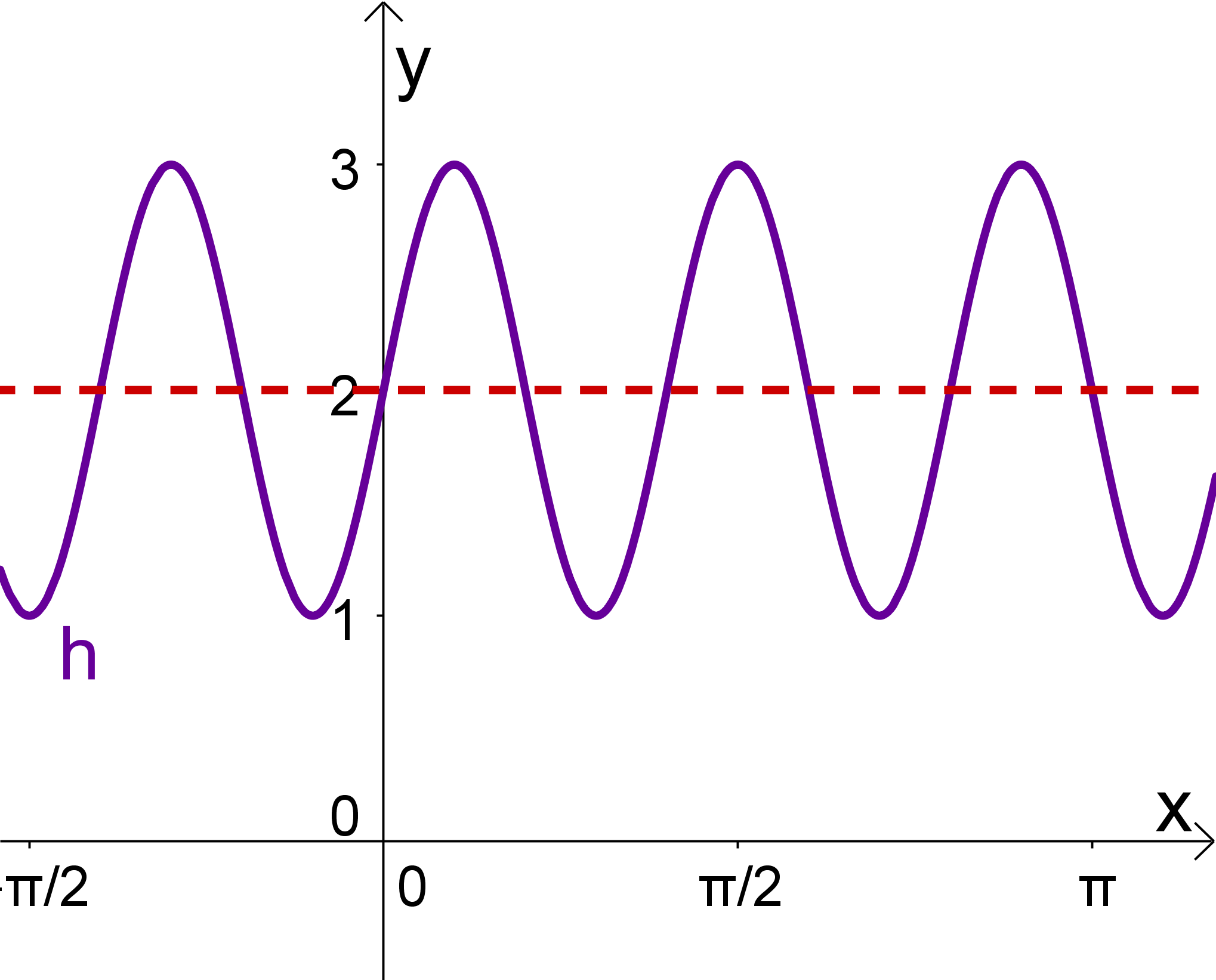
  Als nächstes findest du die Art der Funktion heraus. Handelt es sich bei der Funktion um einen Kosinus oder um einen Sinus?
  Da die Funktion die $y$ -Achse im selben Punkt schneidet wie die Ruhelage, also in $S(0\mid 2),$ handelt es sich um eine Sinusfunktion (beziehungsweise um eine verschobene Kosinusfunktion). Da es die folgenden Schritte erleichtert nehmen wir an, dass es sich um eine Sinusfunktion handelt.
  Die Funktion ist fürs Erste von der Form:
  Der nächste Schritt, den du machst, ist die Bestimmung der Amplitude.
  Da die Extrema jeweils eine Einheit in $y$ -Richtung von der Ruhelage entfernt sind, handelt es sich um die Standard-Sinus-Amplitude.
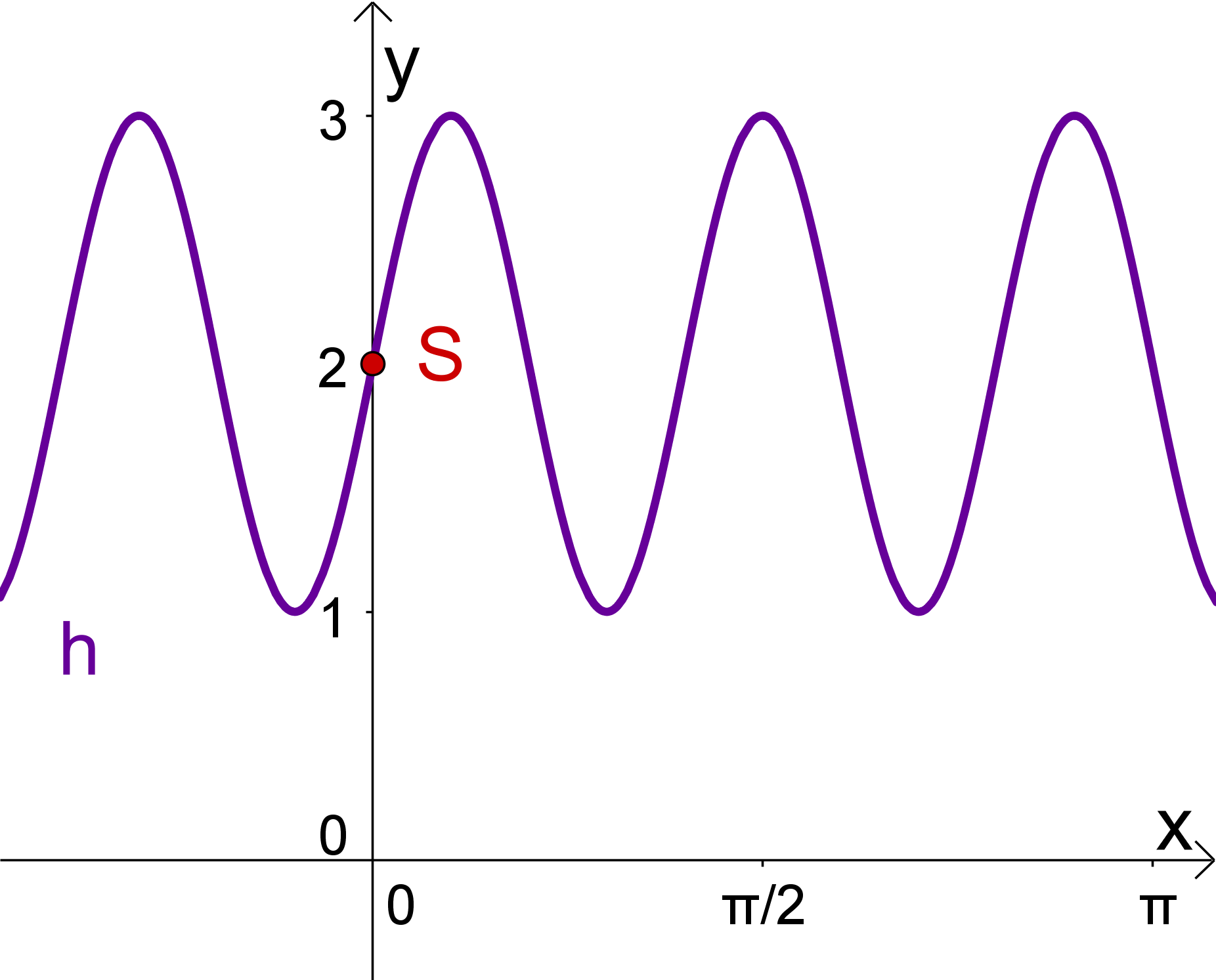
  Da die Amplitude der normalen Amplitude der Sinusfunktion entspricht, bleibt es zunächst bei der Form der Funktion:
  Jetzt fehlt dir nur noch die Periode der Funktion.
  Betrachte dazu zum Beispiel den $x$ -Achsenabschnitt von $0$ bis $\pi$ . In diesem Abschnitt befinden sich $2{,}5$ Perioden der Funktion. Da eine Periode der Standard-Sinus-Funktion von $0$ bis $2\pi$ geht, multiplizieren wir den Wert $2{,}5$ mit $2$ . Damit kommen wir auf den Stauchungsfaktor $5$ .
  Da die Funktion um den Faktor $5$ gestaucht ist, lautet die passende Funktion zu dem Bild:
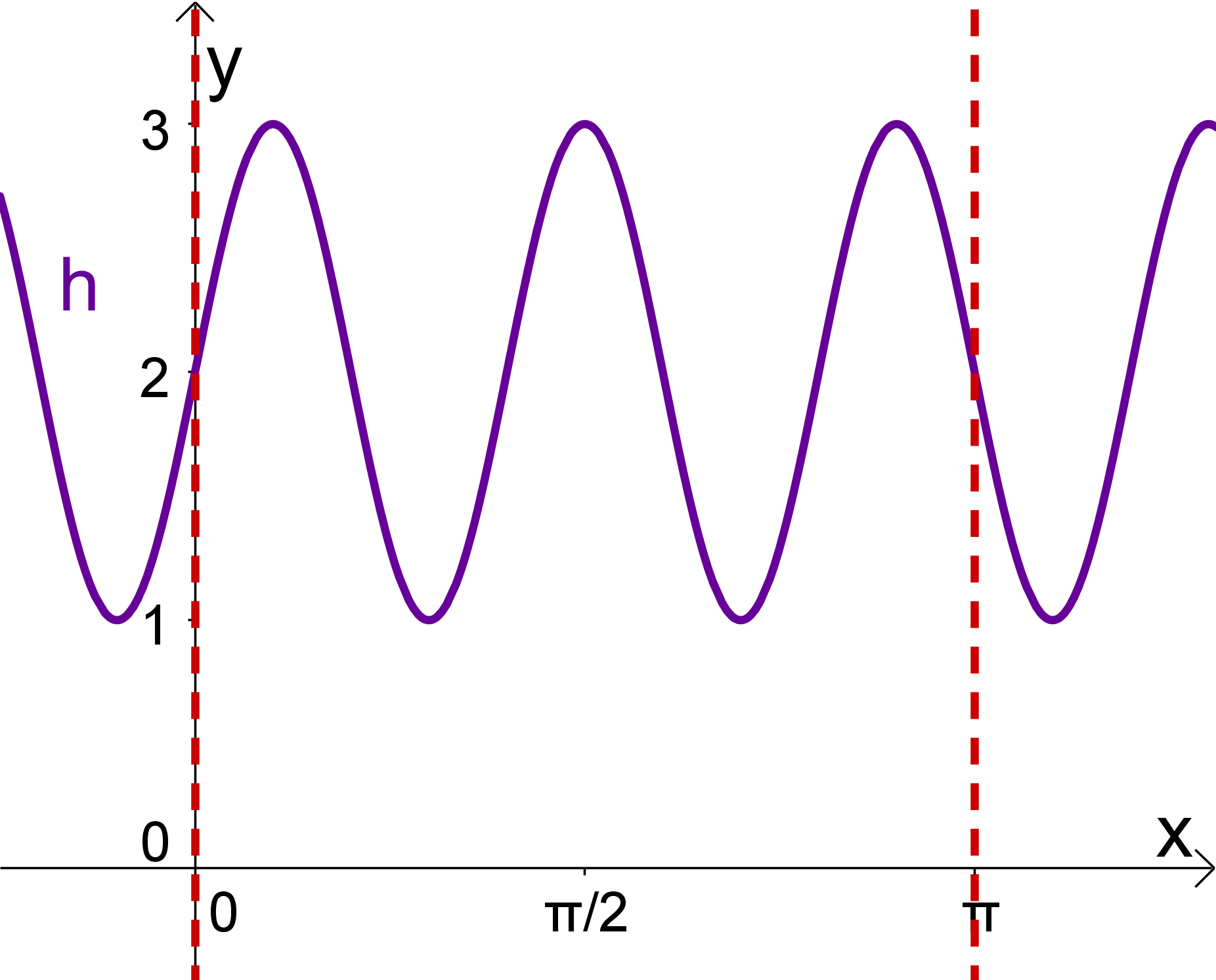
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus- und Kosinusfunktion
  Die Ruhelage der Funktion entspricht der $x$ -Achse.
  Als erstes findest du heraus, ob es sich um eine Sinusfunktion oder eine Kosinusfunktion handelt.
  Die Funktion schneidet die $y$ -Achse weder in einem Extrempunkt, noch im Nullpunkt. Betrachtest du aber die Parallele zur $y$ -Achse durch die Stelle $-1$ auf der $x$ -Achse. Die Funktion schneidet in einem Maximum diese Parallele. Deshalb nehmen wir an, dass es sich um eine verschobene Kosinusfunktion handelt.
  Da die Kosinusfunktion um eine Einheit nach links verschoben ist, lautet die vorläufige Funktion:
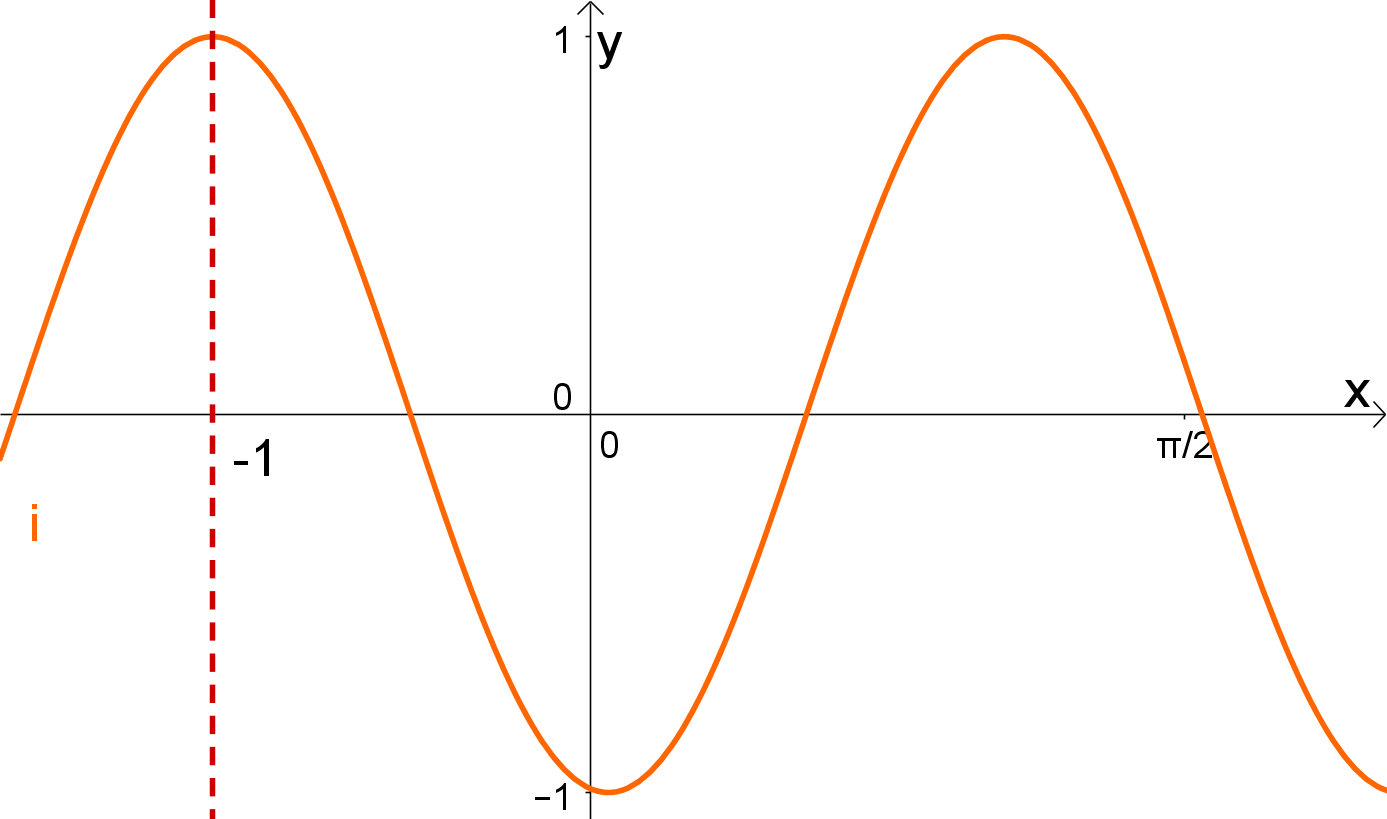
  Jetzt ermittelst du die Amplitude der Funktion.
  Der Abstand der Extrema zu der Ruhelage hat den Wert $1$ , also wird an der Amplitude der Funktion nichts geändert.
  Die Amplitude ist bei der Funktion nicht manipuliert.
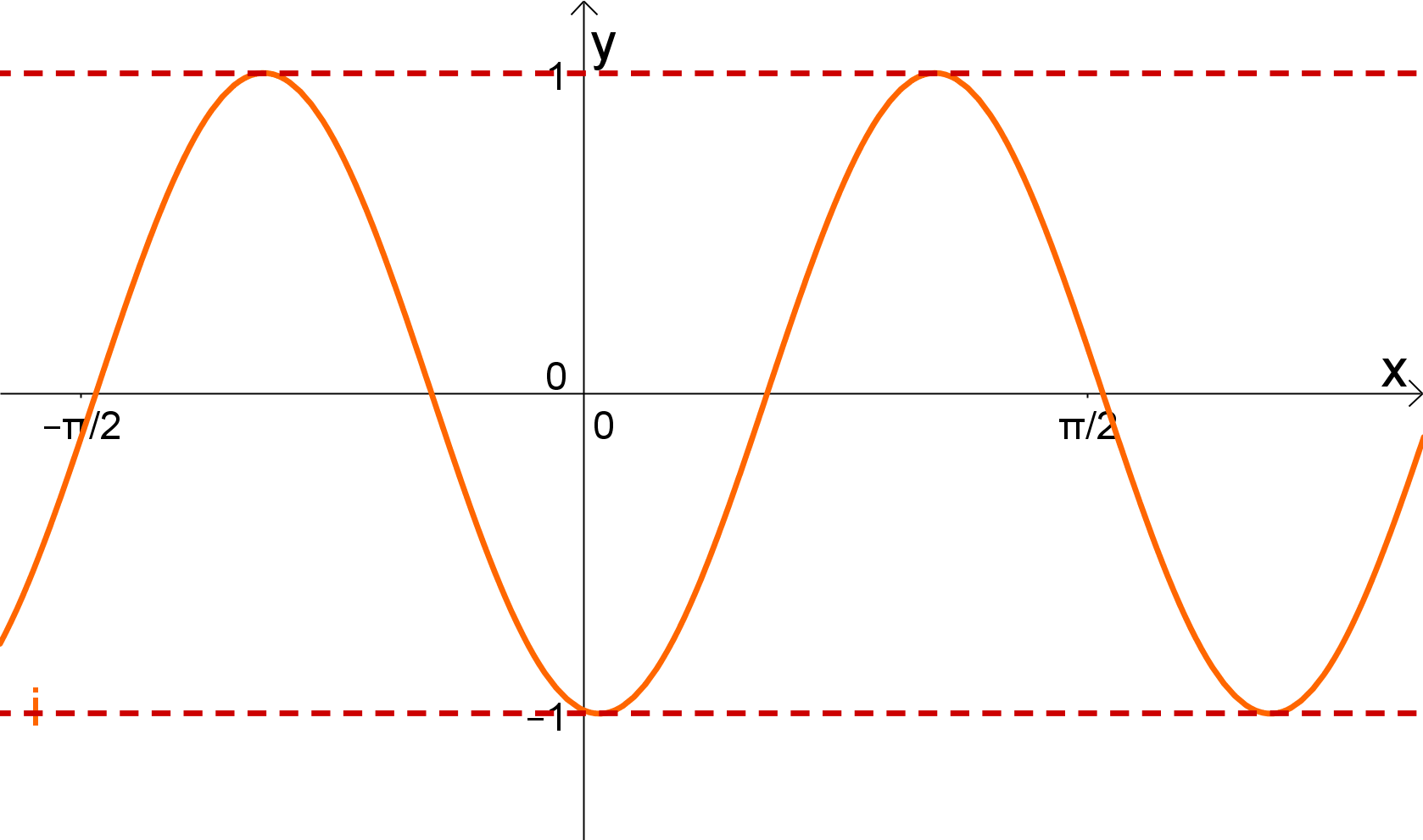
  Als letztes fehlt dir nur noch die Periode der Funktion.
  Dazu betrachten wir ein Intervall der Länge $\pi$ das von $-1$ nach rechts verläuft. In diesem Intervall befinden sich $1{,}5$ Perioden der Funktion, also $3$ in einem Intervall von $2\pi$ . Da $2\pi$ die Periode der Standard-Kosinus-Funktion ist, ist die Funktion um den Faktor $3$ gestaucht.
  Da die Funktion um den Faktor $3$ gestaucht ist, lautet sie:
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Ordne folgendem Graphen die richtige Funktionsgleichung zu:
$f(x)=4\cdot\sin(x)$
$f(x)=4\cdot\cos(x)$
$f(x)=5\cdot\cos(x)$
$f(x)=12\cdot\sin(x)$
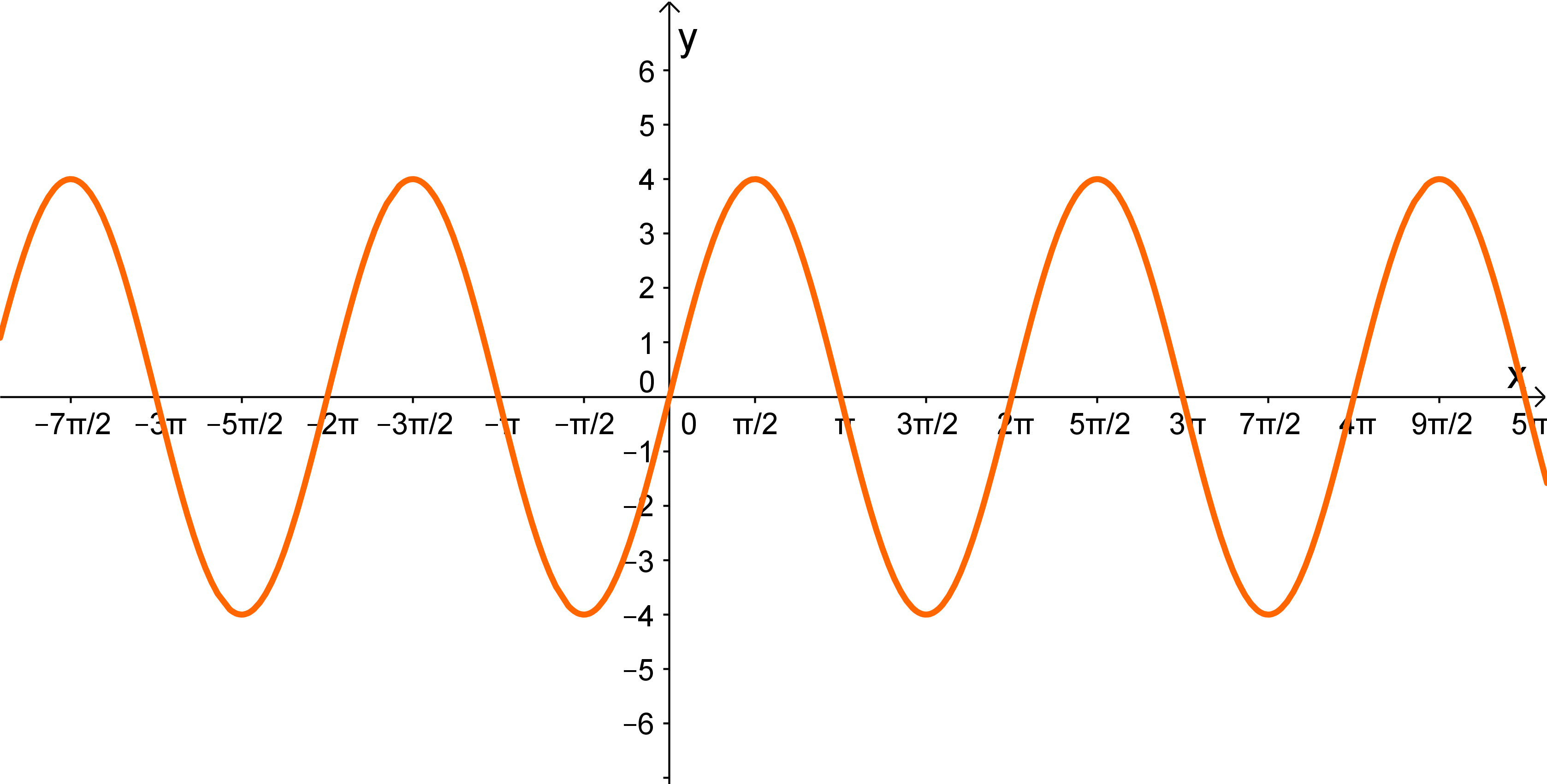
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus- und Kosinusfunktion
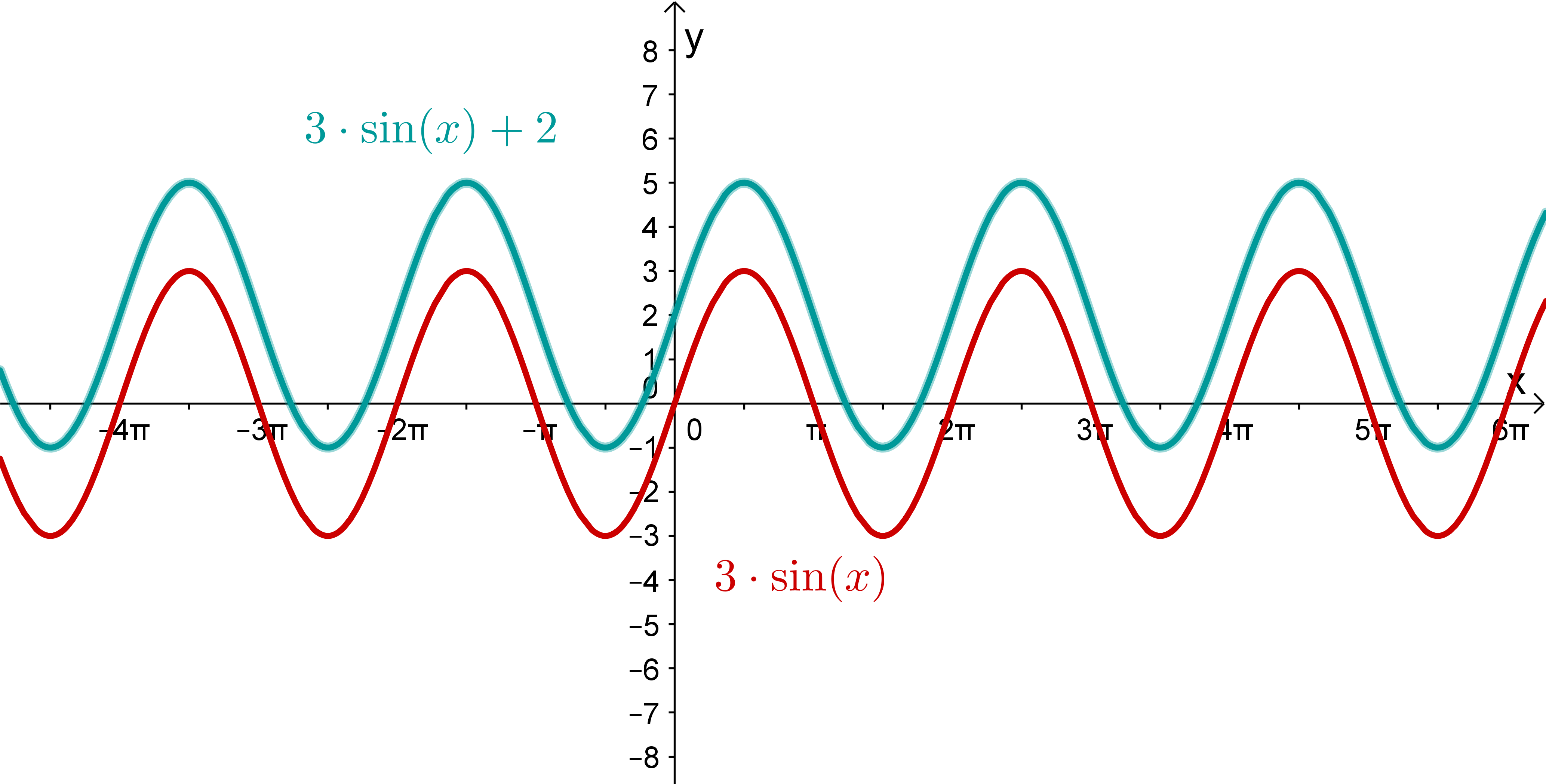
Betrachtest du den Graphen der Funktion, siehst du gleich, dass es sich nicht um eine Kosinus-Funktion handeln kann, da die Kosinus-Funktion achsensymmetrisch bezüglich der y-Achse ist und der Graph der gesuchten Funktion ist punktsymmetrisch bezüglich des Ursprungs. Deshalb kannst du direkt die Funktionen $4\cdot\cos(x)$ und $5\cdot\cos(x)$ ausschließen.
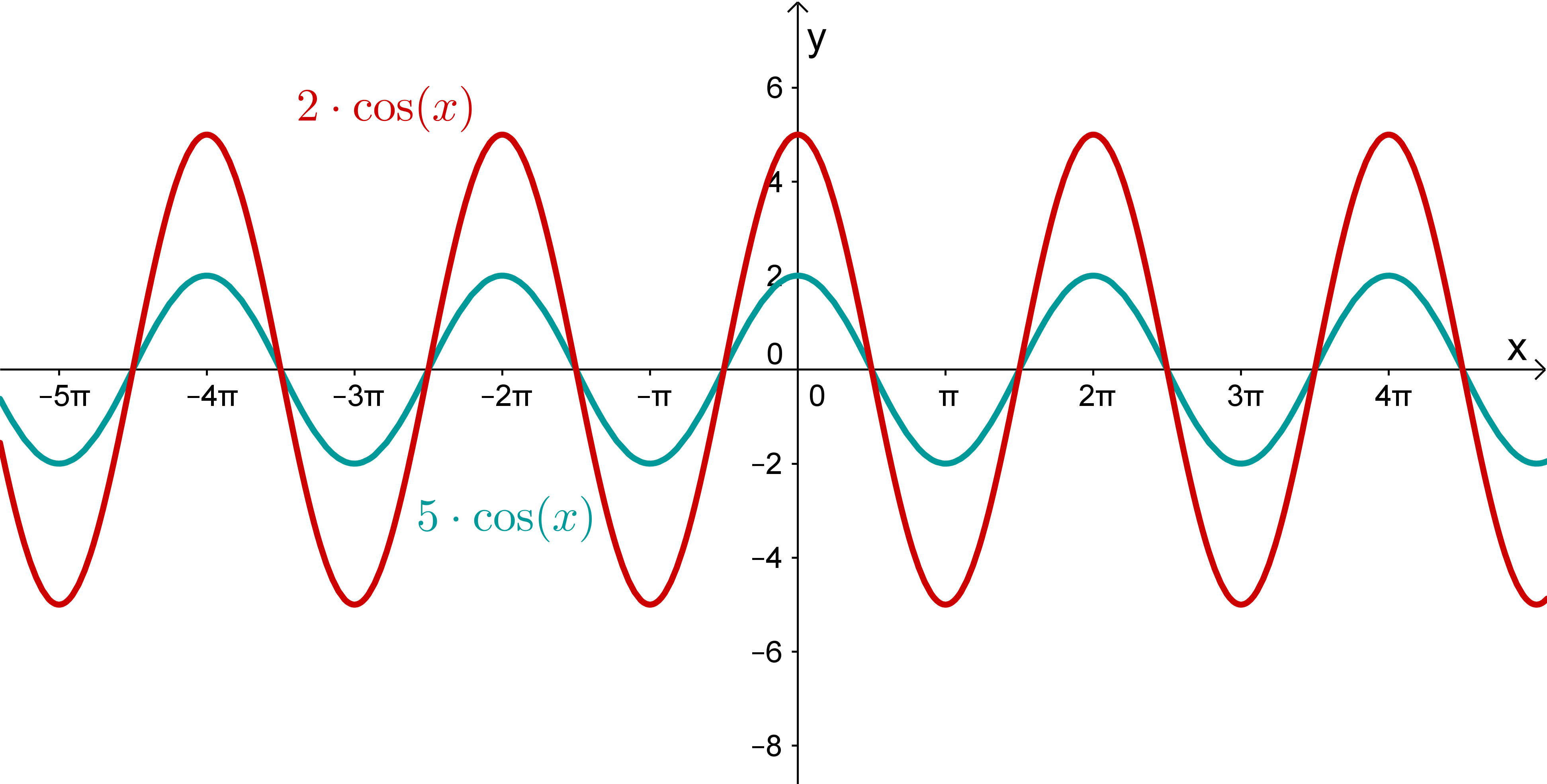
Bleiben also noch die beiden Sinus-Funktionen zur Auswahl. Betrachtest du die Funktion $12\cdot\sin(x)$ , sollte dir auffallen, dass die Amplitude dieser Funktion sehr viel größer ist als die der gesuchten Funktion.Die Amplitude der Funktion $12\cdot\sin(x)$ beträgt 12, da sie $12$ mal so groß ist wie die der normalen Sinus-Funktion $\sin(x)$ .
Die Amplitude des Graphen der gesuchten Funktion, beträgt $4$ , also $4$ mal so groß wie die der normalen Sinus-Funktion $\sin(x)$ . Deshalb ist die gesuchte Funktion $4\cdot\sin(x)$
3
Ordne folgendem Graphen die richtige Funktionsgleichung zu:
$f(x)=3\cdot\cos(x) + 2$
$f(x)=3\cdot\sin(x)$
$f(x)=3\cdot\sin(x)+2$
$f(x)=3\cdot\cos(x)-3$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Verschieben und Strecken von Sinus und Kosinus
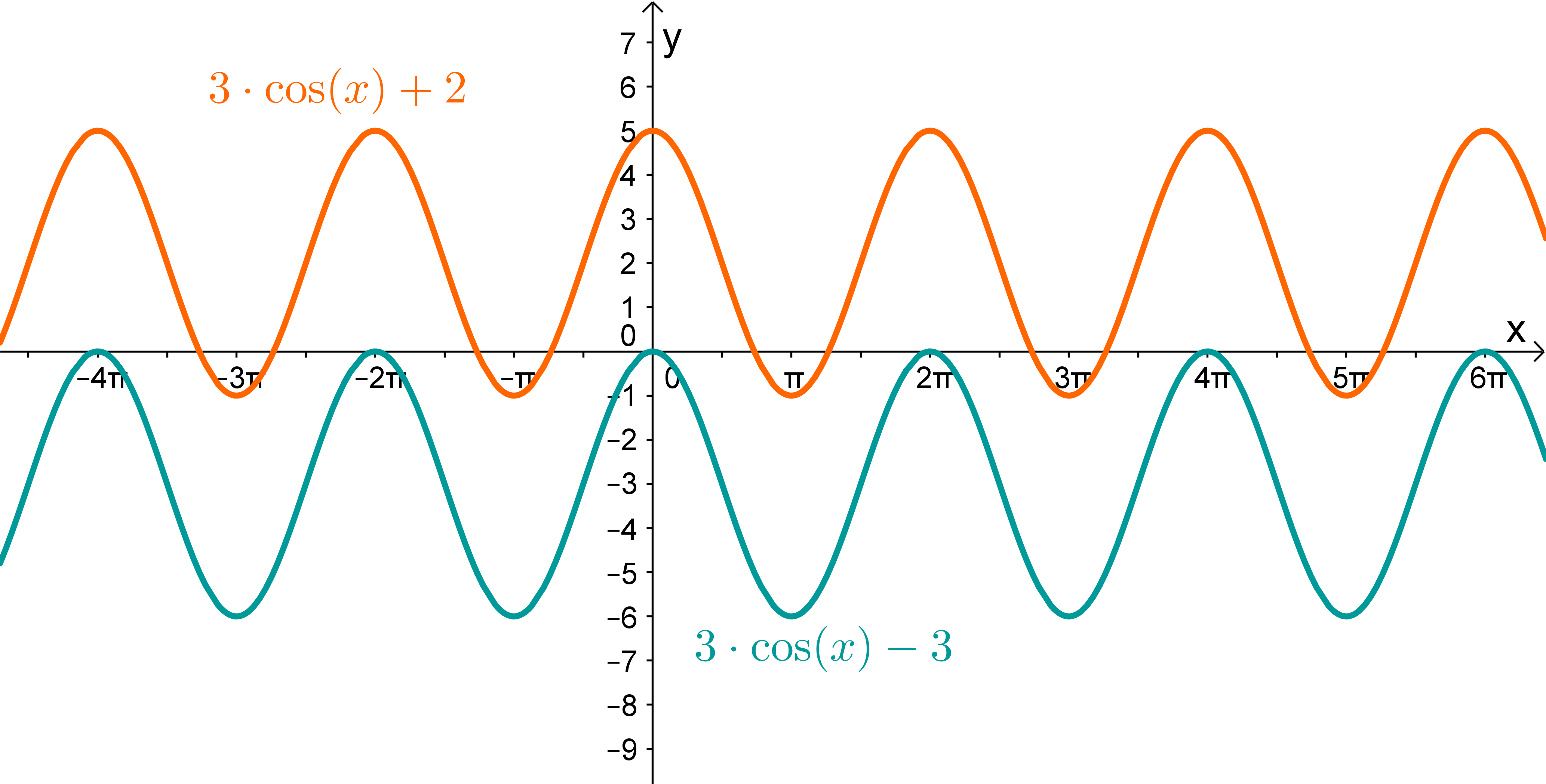
Du siehst das der Graph der gesuchten Funktion achsensymmetrisch bezüglich der $y$ -Achse ist. Nachdem die $\sin(x)$ -Funktion punktsymmertrisch ist, kannst du direkt die Funtkionen $3\cdot\sin(x)$ und $3\cdot\sin(x)+2$ ausschließen.
Betrachtest du nun die Kosinus-Funktionen, musst du nach einer Funktion suchen, deren Ruhelage um $2$ nach oben verschoben ist, weil die Mitte zwischen dem höchsten und niedrigsten Punktes der gesuchten Funktion $(5+(-1)):2=2$ ist.
Außerdem muss die Amplitude der gesuchten Funktion $3$ betragen, denn der größte Abstand zwischen Ruhelage und einem Funktionswert beträgt $3$ . Wegen diesen beiden Eigenschaften kannst du direkt die Funktion $3\cdot\cos(x)-3$ ausschließen, denn dort ist die Ruhelage bei $y=-3$ . Die gesuchte Funktion ist also: $3\cdot\cos(x)+2$
4
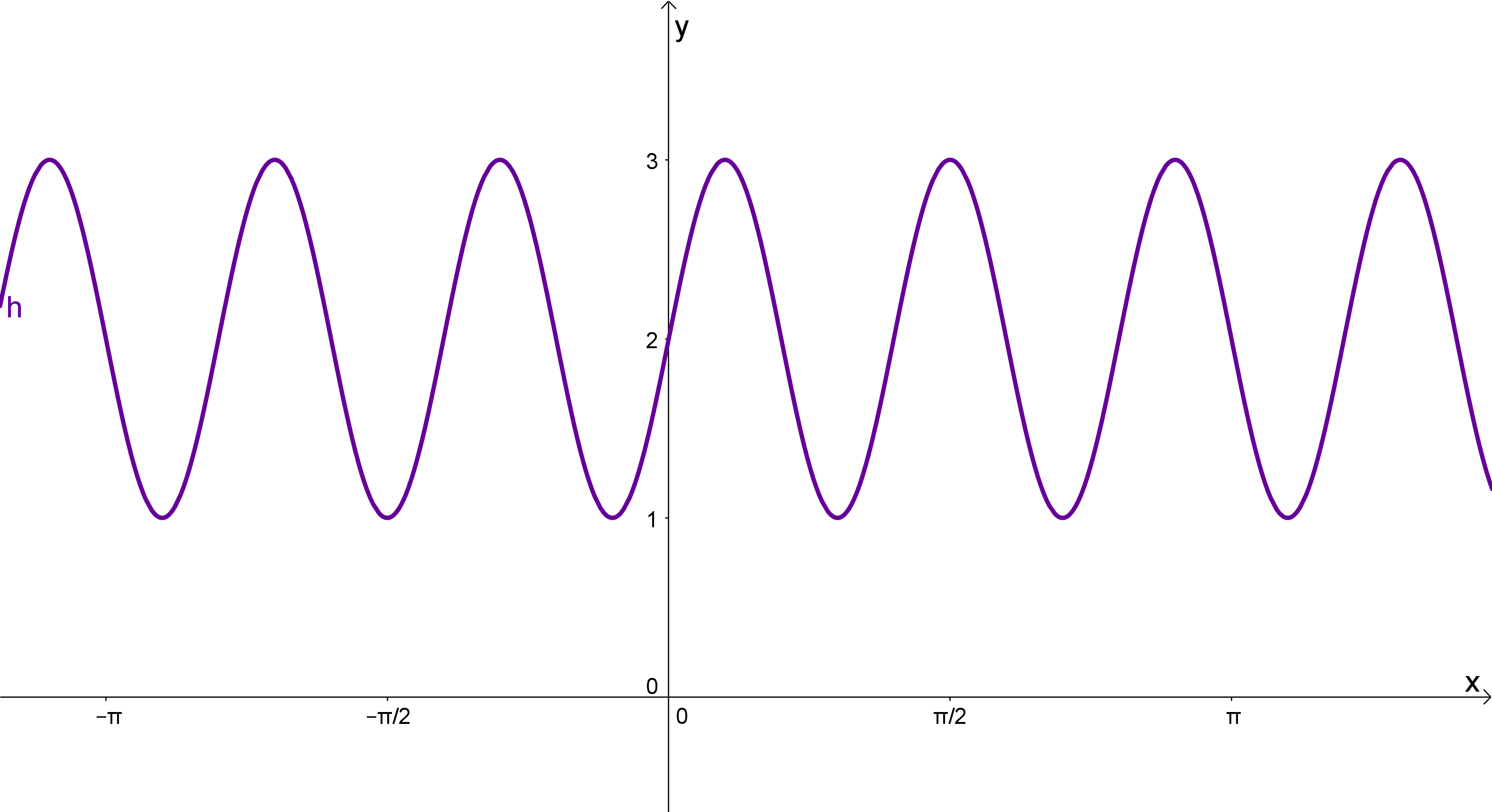
Zeichne die Funktion $f$ mit der Gleichung $f\left(x\right)=3\cdot\sin\left(\frac34(x-\mathrm\pi)\right)$ in ein Koordinatensystem.

Tipp: Schau dir hierfür nochmal die Regeln zum Verschieben und Strecken der Sinus- und Kosinusfunktion an.
Suche als Erstes den Startpunkt deines Graphen; dieser liegt bei $\mathrm\pi$ .
Jetzt musst du nur noch die Periode $T$ herausfinden. Diese bestimmst du mit der Bedingung $2\mathrm\pi = \frac34 \cdot T$ . Du erhältst in diesem Fall also $T = \frac83\mathrm\pi$ .
Nun kannst du die Sinusfunktion zeichnen,allerdings mit einer Amplitude von $3$ statt von $1$ .
5
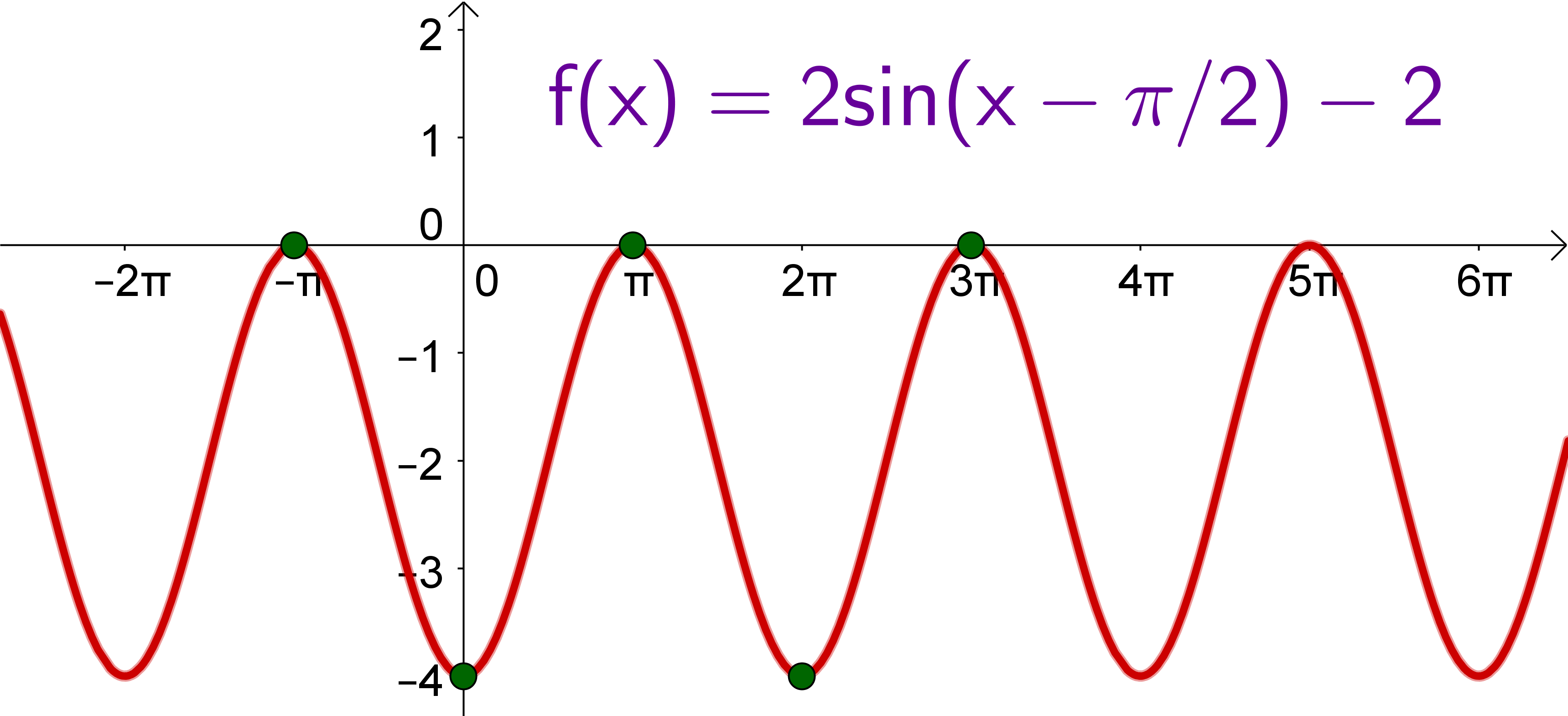
Zeichne im Definitionsbereich $\lbrack-\mathrm\pi,3\mathrm\pi\rbrack$ die manipulierte Sinusfunktion $f(x)=2\cdot\sin(x-\frac{\mathrm\pi}2)-2$ und lies ihren Wertebereich, Nullstellen und Extremstelle ab.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinusfunktion
Tipp: Schau hierfür nochmal die Regeln zum Verschieben und Strecken der Sinus- und Kosinusfunktion an.
Suche als Erstes den Startpunkt deiner Sinusfunktion. Dieser liegt auf der $x-$ Achse bei $+\frac{\mathrm\pi}2$ und auf der $y-$ Achse bei $-2$ . Zeichne von diesen Punkt eine Sinuskurve, allerdings mit der Höhe von $2$ statt $1$ . Danach musst du nur noch die gesuchten Werte ablesen:
Wertebereich: $[-4{,}0]$
Nullstellen: $-\mathrm\pi; \mathrm\pi; 3\mathrm\pi$
Extremstellen: $-\mathrm{\pi};0;\mathrm{\pi};2\mathrm{\pi};3\mathrm{\pi}$
6
Zeichne im Definitionsbereich $\lbrack0,\frac{5\mathrm\pi}2\rbrack$ die manipulierte Sinusfunktion $f(x)=-\sin(x-\mathrm\pi)$ und lies ihren Wertebereich, Nullstellen und Extremstelle ab.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus- und Kosinusfunktion
Tipp: Schau hierfür nochmal die Regeln zum Verschieben und Strecken der Sinus- und Kosinusfunktion an.
Suche als Erstes den Startpunkt deiner Sinusfunktion. Dieser liegt auf der x−Achse bei $+\mathrm\pi$ und auf der y−Achse bei $0$ . Zeichne von diesen Punkt eine Sinuskurve, allerdings, durch das Minus vor der Funktion, genau umgekehrt. Also zeichne die Sinuskurve als Erstes nach unten. Danach musst du nur noch die gesuchten Werte ablesen:
Wertebereich: $[-1;1]$
Nullstellen: $0,\mathrm\pi,2\mathrm\pi$
Extremstellen: $\frac{\mathrm\pi}2,\frac{3\mathrm\pi}2,\frac{5\mathrm\pi}2$
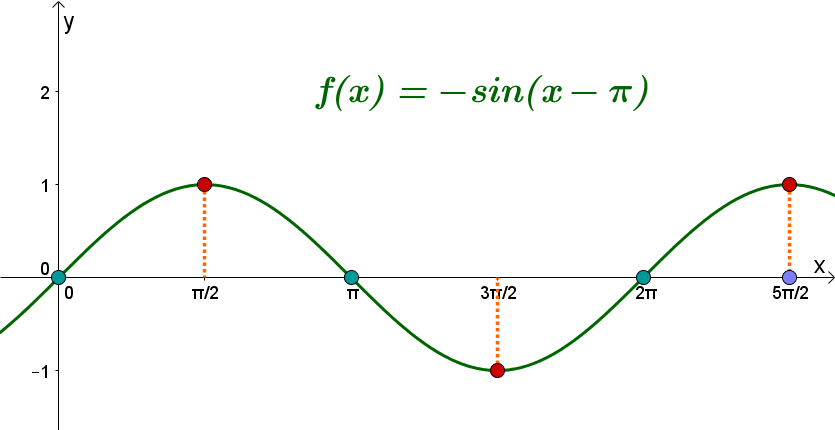
7
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Notiere eine Wertetabelle, zeichne den Graphen und beobachte, wie sich jeweils der Graph im Vergleich zur Funktonsgleichung $y=\cos\left(x\right)$ ändert.
1. $y=\cos\left(x\right)+1$ . Formuliere: " $+1$ " bewirkt…
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verschieben und Strecken von trigonometrischen Funktionen
  $+1$ bewirkt die Verschiebung des Graphen entlang der y-Achse in positiver Richtung um den Betrag $\left|1\right|$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $y=\cos\left(x+\frac\pi2\right)$ . Formuliere: " $+\frac{\mathrm\pi}2$ " beim $x$ -Wert bewirkt…
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verschieben und Strecken von trigonometrischen Funktionen
  $+\frac{\mathrm\pi}2$ bewirkt die Verschiebung des Graphen entlang der x-Achse in negative Richtung um den Betrag $\left|\frac{\mathrm\pi}2\right|$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $y=2\cdot\cos\left(x\right)$ . Formuliere: " $\cdot2$ " bewirkt…
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verschieben und Strecken von trigonometrischen Funktionen
  $\cdot2$ bewirkt die Streckung des Graphen entlang der y-Achse, sowie die Veränderung des Amplitudenausschlags.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $y=\cos\left(2x\right)$ . Formuliere: " $\cdot2$ " beim $x$ -Wert bewirkt…
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Verschieben und Strecken von trigonometrischen Funktionen
  $\cdot2$ bewirkt die Stauchung des Graphen entlang er x-Achse sowie der Veränderung der Periodenlänge von $2\pi\;$ zu $\pi$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉