Eine Schaustellerfamilie ist seit Jahrzehnten mit ihrer Achterbahn auf Volksfesten vertreten. Nun bestellt sie bei einem Hersteller ein neues Modell.
Sie erhält für den Aufstiegsteil der Bahn das abgebildete (nicht maßstabsgetreue) Angebot.
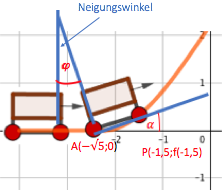
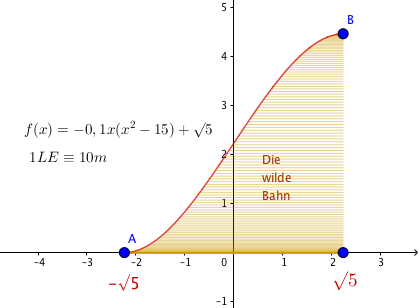
Der zahnradbetriebene Aufstiegsteil dem die Mittelpunkte der Wagenräder folgen, beginnt demnach nach einer kurzen horizontalen Fahrt ohne Knick im Punkt und verläuft von da an nach der Funktion
bis zum höchsten Achterbahnpunkt , ab dem sich (wieder ohne Knick) eine kurze horizontale Strecke bis zur ersten Abfahrt anschließt.
Im Familienkreis wird über das Angebot beraten.
Der Seniorchef legt Wert darauf, dass die bisherige Achterbahnhöhe von 40 m von der neuen Bahn deutlich übertroffen wird.
Sagt ihm das Angebot zu?
Der Juniorchef ist als Ingenieur für die Sicherheit und den Energiebedarf der Bahn zuständig.
Er möchte, dass die mittlere Steigung der Aufstiegsstrecke, die für den Energiebedarf der Bahn maßgeblich ist, den Wert 1 nicht übersteigt.
Außerdem möchte er wissen, in welchen Punkten der Aufstiegsstrecke die lokale Steigung gleich der mittleren Steigung ist.
Berechne die jeweiligen Werte.
Aus Sicherheitsgründen für die Passagiere liegt ihm auch daran, dass im steilsten Punkt des Aufstiegs der lokale Steigungswinkel kleiner als 60° ist.
Hat er einen Einwand?
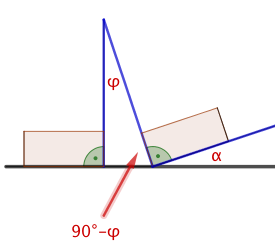
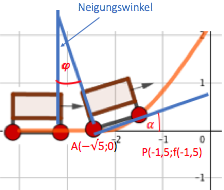
Außerdem möchte er sichergehen, dass der Neigungswinkel zwischen zwei knapp hintereinander gekoppelten Wagen kleiner als 25° ist, damit sich die Aufbauten der Wagen nicht berühren.
Er berechnet diesen Winkel für die Situation, bei der sich die Vorderachse des ersten Wagens am Punkt und die Hinterachse am Punkt befindet.
Wie groß ist dieser Winkel?
Die Enkelin des Seniorchefs ist als Marketingleiterin von der Idee der Herstellerfirma begeistert, unter die Aufstiegsstrecke von bis ein Werbebanner zu spannen.
Dessen Kosten veranschlagt der Hersteller mit 3000.-€ für die Befestigung und 8,50€ pro Quadratmeter für die Materialkosten. Die Familie ist allerdings nicht bereit, mehr als 10000.-€ für das Banner auszugeben.
Wird das Banner bestellt?
Die Urenkelin des Seniorchefs ist Abiturientin und empfiehlt der Familie eine bescheidenere Vegrößerung der Bahn.
Sie rät, eine Aufstiegsfunktion der Form
so zu wählen, dass sich als Startpunkt des Aufstiegsteils der Bahn und die größte lokale Steigung im Punkt mit einem Steigungswinkel von 45° ergibt.
Die Berechnung von g(x) bereitet ihr keine Probleme.
Welche Höhe hätte die neue Achterbahn nach ihrem Vorschlag?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?