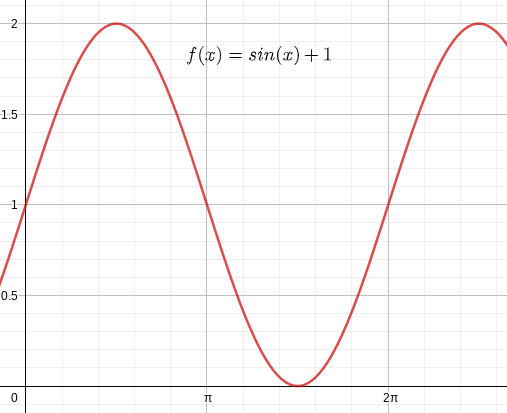
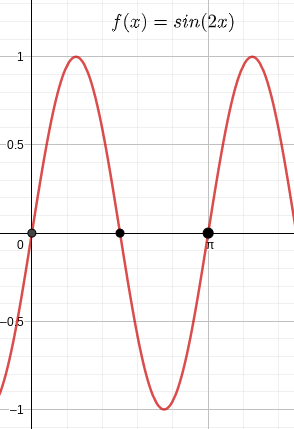
Analysis, Teil A, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion $f : x \mapsto \frac{x}{\ln x}$ mit Definitionsmenge $ℝ^{+} \ {1}$ . Bestimmen Sie Lage und Art des Extrempunktes des Graphen von $f$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnung von Extremwerten
Um zu berechnen, ob es die Funktion Extremwerte hat braucht man die 1. Ableitung dieser Funktion.
$f^{'} (x) = \frac{(x)^{'} \cdot (l n x) - (x) \cdot (l n x)^{'}}{(l n x)^{'})^{2}}$
$f^{'} (x) = \frac{1 \cdot (l n x) - x \cdot \frac{1}{x}}{(\frac{1}{x})^{2}}$
$f^{'} (x) = \frac{l n x - \frac{x}{x}}{\frac{1}{x^{2}}}$
$f^{'} (x) = \frac{l n x - 1}{\frac{1}{x^{2}}}$
$f^{'} (x) = (l n x - 1) \cdot x^{2}$
$f^{'} (x) = x^{2} l n x - x^{2}$
$f^{'} (x) = 0$
??
$\Rightarrow$ $x_{E 1} = 0$ aber außerhalb des Definitionsbereichs
$\Rightarrow$ $x_{E 2} = 1$
Die 2. Ableitung berechnen:
$f^{''} (x) = ((l n x - 1) \cdot x^{2})^{'}$
$f^{''} (x) = \frac{1}{x} \cdot x^{2} + l n x \cdot 2 x$
$f^{''} (x) = \frac{x^{2}}{x} + 2 x l n x$
$f^{''} (x) = x + 2 x l n x$
$x_{E}$ in $f^{''} (x)$ einsetzten:
$f^{''} (x_{E}) = 0 + 2 \cdot 0 \cdot l n 0 = 2 \cdot 0 + 1 = 0 + 0 = 0$
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die in $ℝ$ definierte Funktion $f$ mit $f (x) = e^{x} \cdot (2 x + x^{2})$ .
1. Bestimmen Sie die Nullstellen der Funktion $f$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen
  $f (x) = e^{x} \cdot (2 x + x^{2}) = 0$
  $e^{x}$ kann nicht $0$ sein
  $\Rightarrow$ $2 x + x^{2} = 0$ | $- 2 x$
  $x^{2} = - 2 x$ | $: x$
  $x = - 2$
  $2 x = 0$
  $x = 0$
  $x^{2} = 0$
  $x = 0$
  $\Rightarrow$ $x_{1} = - 2$
  $x_{2} = 0$
  Die Nullstellen liegen bei $x = - 2$ und $x = 0$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Zeigen Sie, dass die in $ℝ$ definierte Funktion $F$ mit $F (x) = x^{2} \cdot e^{x}$ eine Stammfunktion von $f$ ist. Geben Sie eine Gleichung einer weiteren Stammfunktion $G$ von $f$ an, für die $G (1) = 2 \cdot e$ gilt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen
  $\int_{}^{} f (x) d x$
  $=$ $\int_{}^{} e^{x} \cdot (2 x + x^{2}) d x$
  $=$ $\int_{}^{} (2 x + x^{2}) \cdot e^{x} d x$
  $=$ $((2 x + x^{2}) \cdot e^{x}) - \int_{}^{} (2 x + x^{2})^{'} \cdot e^{x} d x$
  $=$ $((2 x + x^{2}) \cdot e^{x}) - ((2 + 2 x) \cdot e^{x})$
  $=$ $e^{x} \cdot ((2 x + x^{2}) - (2 + 2 x))$
  $=$ $e^{x} \cdot (2 x + x^{2} - 2 - 2 x)$
  $=$ $e^{x} \cdot (x^{2} + 2 x - 2 x - 2)$
  $=$ $e^{x} \cdot (x^{2} - 2)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben sind die in $ℝ$ definierten Funktionen $g_{a, c} : x \mapsto \sin (a x) + c$ mit $a, c \in ℝ_{0}^{+}$ .
1. Geben Sie für jede der beiden folgenden Eigenschaften einen möglichen Wert für $a$ und einen möglichen Wert für $c$ so an, dass die zugehörige Funktion $g_{a, c}$ diese Eigenschaft besitzt.
  $α)$ Die Funktion $g_{a, c}$ hat die Wertemenge $[0; 2]$ .
  $β)$ Die Funktion $g_{a, c}$ hat im Intervall $[0; π]$ genau drei Nullstellen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktion
  $α$ ) Wenn man einfach die Funktion $f (x) = \sin (x)$ . Diese hat die Wertemenge $[- 1; 1]$ . Um also die Wertemenge auf $[0; 2]$ zu kommen muss man zur Funktion $f (x) = \sin (x)$ $1$ dazuaddieren.
  $\Rightarrow$ $c = 1$
  $a$ hingegen kann man frei wählen, da $a$ innerhalb der Sinusfunktion steht und somit nur einen Effekt auf die Periode hat.
  $β$ ) Wie schon bei $α$ ) gesagt, ist $a$ für die Periode also auch für die Nullstellen der Funktion verantwortlich. Die Funktion $s i n (x)$ hat in ganzahliegen $π$ -Intervallen (z.B.: $[0; π], [2 π; 3 π]$ ) immer zwei Nullstellen. Deshalb muss man den Koeffizienten von $x$ , $a$ , um eins erhöhen um eine weitere Nullstelle in diesem Intervall ( $[0; π]$ ) zu erhalten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ermitteln Sie in Abhängigkeit von $a$ , welche Werte die Ableitung von $g_{a, c}$ annehmen kann.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktion
  Die Ableitung der Funktion $f (x) = s i n (a x) + c$ ist
  $f^{'} (x) = \cos (a x) \cdot a$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Abbildung zeigt den Graphen einer Funktion $f$ .
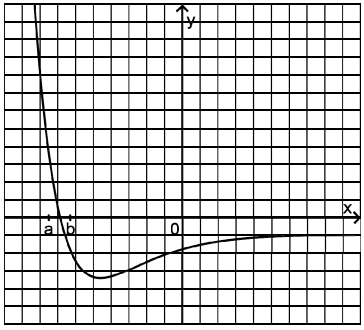
1. Beschreiben Sie für $a \leq x \leq b$ den Verlauf des Graphen einer Stammfunktion von $f$ .
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktionen
  Nullstellen
  Um die Nullstellen zu bestimmen, muss man die Funktion gleich $0$ setzen.
  $e^{x} \cdot (2 x + x^{2}) = 0$
  Da $e^{x}$ nie $0$ werden kann, muss man nur $2 x + x^{2}$ gleich $0$ setzen.
  $2 x + x^{2} = 0$
  $x \cdot (2 + x)$
  $\Rightarrow x = 0$
  $\Rightarrow 2 + x = 0 \Rightarrow x = - 2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Skizzieren Sie in der Abbildung den Graphen einer Stammfunktion von $f$ im gesamten dargestellten Bereich.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
  Stammfunktion
  $F^{'} (x) = x^{2} \cdot e^{x}$
  $= 2 x \cdot e^{x} + x^{2} \cdot e^{x}$
  $= e^{x} \cdot (2 x + x^{2})$
  $F (1) = e^{1} \cdot (2 \cdot 1 + 1^{2})$
  $= 2 e + 1$
  $\Rightarrow G (x) = x^{2} \cdot e^{x} - 1$
  Man muss in die herausgefundene Stammfunktion $F (x)$ $1$ einsetzten. Dann erkennt man, dass der Unterschied von $F (1)$ zu $G (1)$ eine $+ 1$ bei $F (1)$ ist. Deshalb muss man wieder $1$ subtrahieren um auf den richtigen Wert von $G$ zu kommen. Dies geht, da alle Stammfunktionen sich nur durch die Verschiebung auf der y-Achse unterscheiden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

	$\int_{}^{} f (x) d x$
$=$	$\int_{}^{} e^{x} \cdot (2 x + x^{2}) d x$
$=$	$\int_{}^{} (2 x + x^{2}) \cdot e^{x} d x$
$=$	$((2 x + x^{2}) \cdot e^{x}) - \int_{}^{} (2 x + x^{2})^{'} \cdot e^{x} d x$
$=$	$((2 x + x^{2}) \cdot e^{x}) - ((2 + 2 x) \cdot e^{x})$
$=$	$e^{x} \cdot ((2 x + x^{2}) - (2 + 2 x))$
$=$	$e^{x} \cdot (2 x + x^{2} - 2 - 2 x)$
$=$	$e^{x} \cdot (x^{2} + 2 x - 2 x - 2)$
$=$	$e^{x} \cdot (x^{2} - 2)$

Analysis, Teil A, Aufgabengruppe 1

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?