Aufgaben zu Schnittpunkte berechnen
- 1
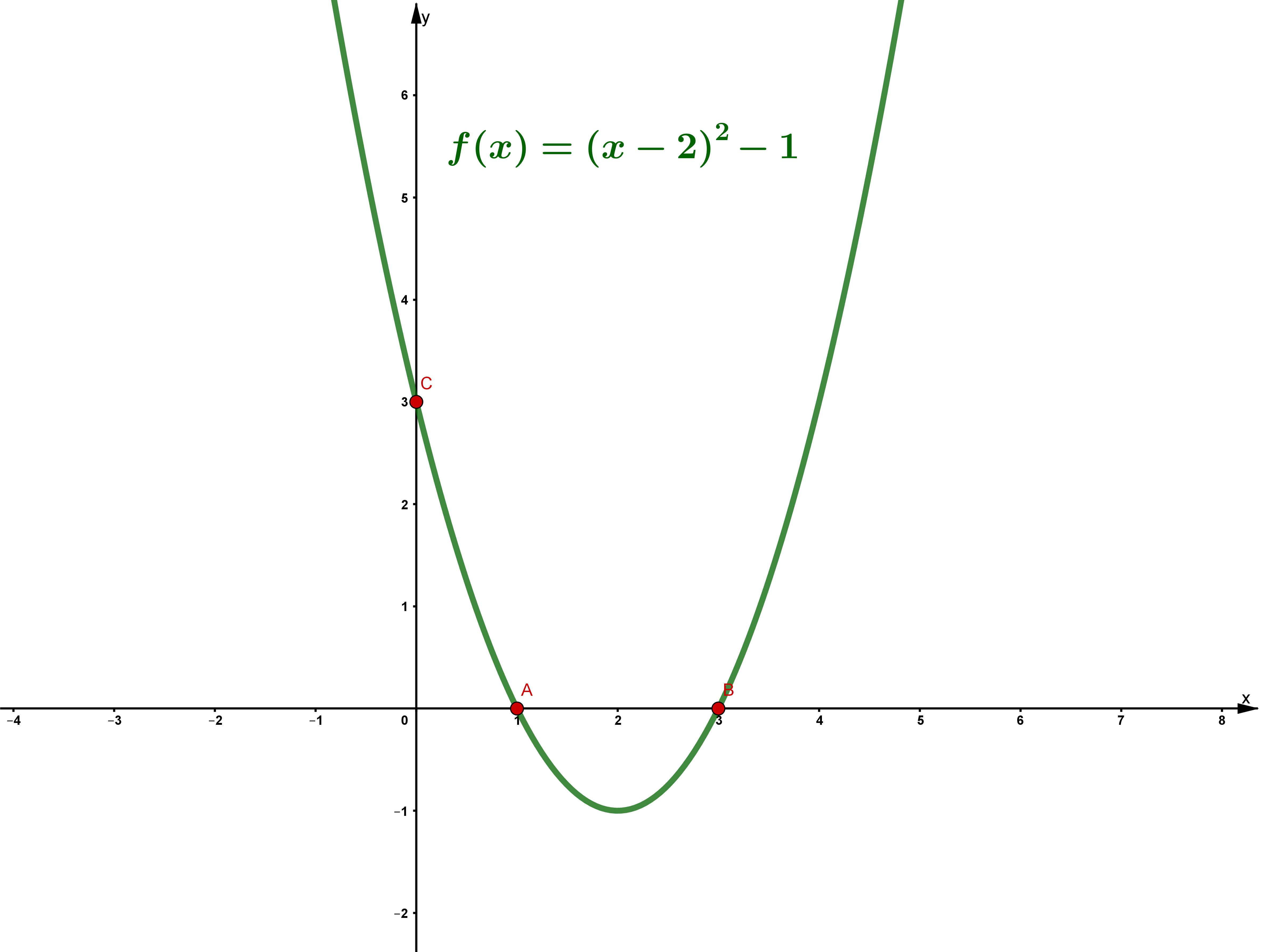
Bestimme bei folgenden Funktionen die Schnittpunkte mit den Koordinatenachsen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Um die Schnittpunkte mit den Koordinatenachsen zu berechnen, wird eine der Variablen in der Funktion (, ) gleich gesetzt.
Schnittpunkte mit der x-Achse
Die Schnittpunkte mit der -Achse sind die Nullstellen der Funktion.Man erhält sie, indem man die Funktion bzw. den -Wert gleich Null setzt.
Die Schnittpunkte mit der -Achse liegen bei und .
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der -Achse zu ermitteln, muss für den -Wert eingesetzt werden.
Der Schnittpunkt mit der -Achse liegt bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Um die Schnittpunkte mit den Koordinatenachsen zu berechnen, wird eine der Variablen in der Funktion (, ) gleich gesetzt.
Schnittpunkte mit der x-Achse
Die Schnittpunkte mit der -Achse sind die Nullstellen der Funktion.Man erhält sie, indem man die Funktion bzw. den -Wert gleich Null setzt.
↓ Kleinste Potenz von ausklammern.
↓ Ein Produkt wir dann Null, wenn einer der Faktoren Null ist.
Setze die Klammer gleich Null.
↓ Mitternachtsformel anwenden.
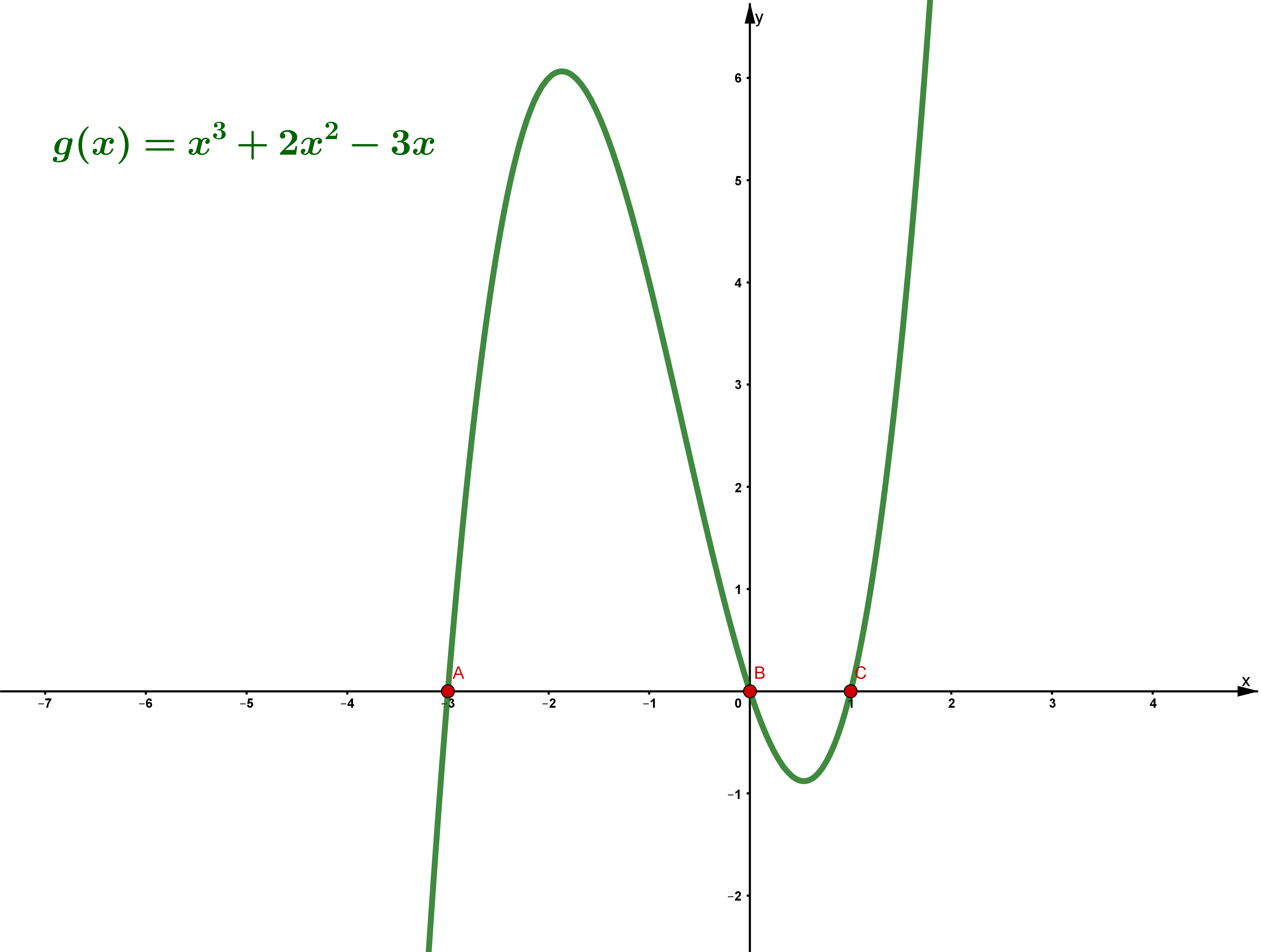
Die Schnittpunkte mit der -Achse liegen bei und und .
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der -Achse zu ermitteln, muss für den -Wert eingesetzt werden.
Der Schnittpunkt mit der -Achse liegt bei .
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Um die Schnittpunkte mit den Koordinatenachsen zu berechnen, wird eine der Variablen in der Funktion (, ) gleich gesetzt.
Schnittpunkte mit der x-Achse
Die Schnittpunkte mit der -Achse sind die Nullstellen der Funktion.Man erhält sie, indem man die Funktion bzw. den -Wert gleich Null setzt.
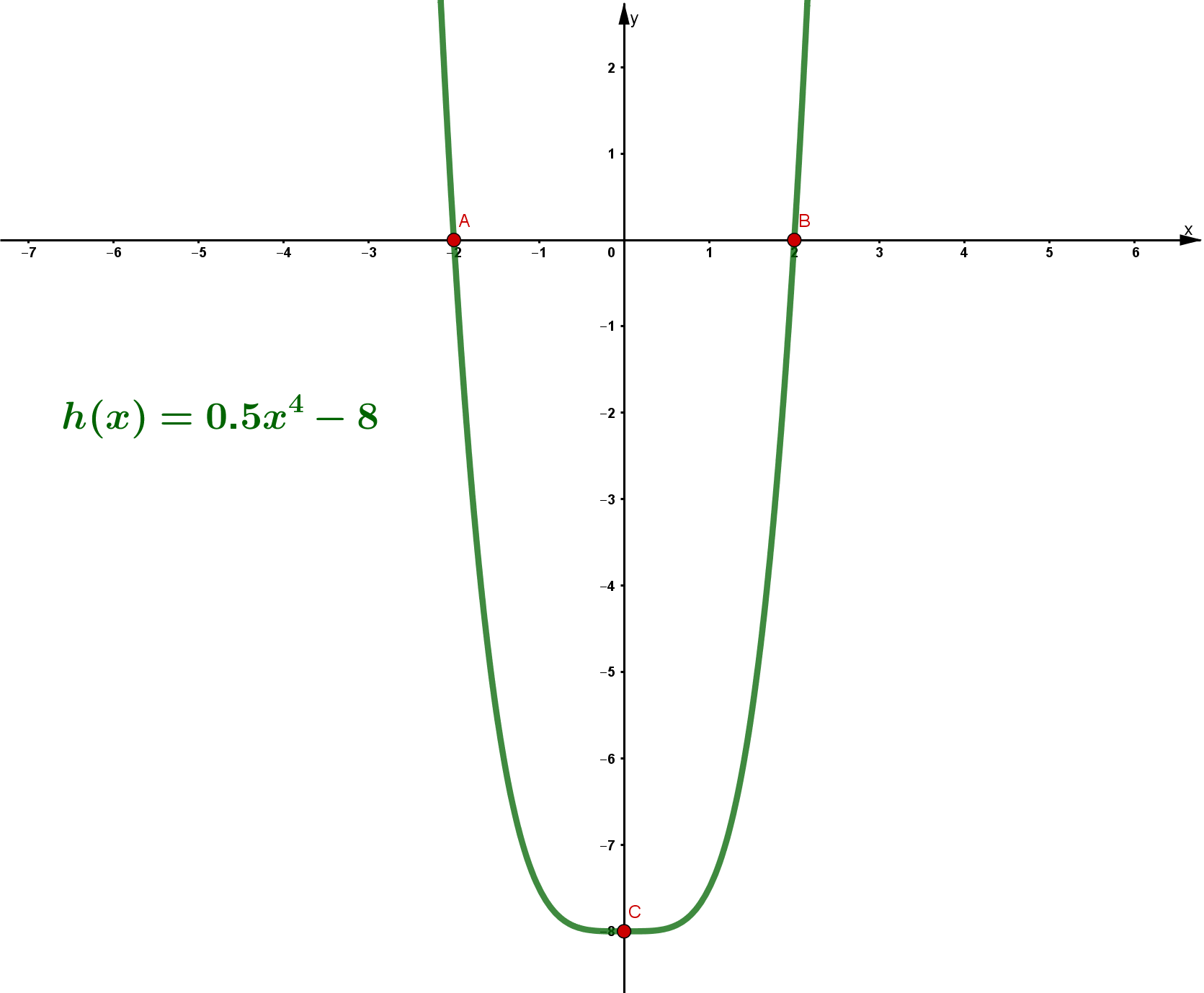
Die Schnittpunkte mit der -Achse liegen bei und .
Schnittpunkt mit der y-Achse
Um den Schnittpunkt mit der -Achse zu ermitteln, muss für den -Wert eingesetzt werden.
Der Schnittpunkt mit der -Achse liegt bei .
Hast du eine Frage oder Feedback?
- 2
Gegeben ist die Gleichung der Geraden
und die Gleichung der ganzrationalen Funktion .
Berechne die Schnittpunkte von und .
Errate dazu eine Lösung der Schnittgleichung und berechne die weiteren Lösungen mit Hilfe der Polynomdivision.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Polynomdivision
Schnittpunkte berechnen
Die beiden Funktionen haben einen Schnittpunkt, wenn sie für einen gleichen x-Wert denselben y-Wert haben. Setze also die Funktionen und gleich. Die Funktionen lauten:
Für Polynome vom Grad 3 musst du eine Nullstelle erraten. Alle weiteren Nullstellen lassen sich dann mit einer Polynomdivision ermitteln.
Eine Nullstelle von ist , denn
Um den ersten Schnittpunkt von und zu bestimmen, kannst du nun entweder in oder einsetzen.
Einsetzen in ergibt:
Der Schnittpunkt ist dann:
Polynomdivision
Wende nun die Polynomdivision auf folgende Gleichung an:
Verbleibende Nullstellen berechnen
Von kannst du nun noch die beiden Nullstellen bestimmen. Nutze hierfür beispielsweise die Mitternachtsformel.
Die Nullstellen von sind also:
weitere Schnittpunkte berechnen
Den zweiten und dritten Schnittpunkt von und , kannst du nun bestimmen, indem du und in oder einsetzt.
Einsetzen in ergibt:
Schnittpunkte
Die Schnittpunkte der beiden Funktionen liegen bei , und .
- 3
Die beiden Funktionen und sind gegeben. Es gilt . Berechne die Schnittpunkte von und .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte von Funktionen
Tipp: Schneiden sich zwei Funktionen haben ihre - und -Koordinaten an diesem Punkt denselben Wert. Folglich muss man beide Funktionen gleichsetzen und auf eine Seite bringen, um nach aufzulösen.
Gleichsetzten der Funktionen
durch Taschenrechner oder Raten einer Nullstelle
Berechnung einer Nullstelle mittels Polynomdivision
Neue Funktion:
Berechnung der restlichen Nullstellen
Auflösen der neuen Funktion nach x:
Da nun unter der Wurzel eine negative Zahl steht, gibt es keine weiteren Lösungen und damit auch keine weiteren -Koordinaten der Schnittpunkte.
Die vorher ausgerechnete -Koordinate ist somit die einzige Koordinate.
Es gibt nur einen Schnittpunkt
Setze den -Wert in eine der beiden Funktionen oder ein.
Der Schnittpunkt der beiden Funktionen liegt bei .
Gleichsetzten beider Funktionen
Auflösen nach Null Polynomfunktion dritten Grades
Berechnung der Nullstellen mittels Polynomdivision
Erhalt einer Nullstelle für
Berechnung des -Werts durch Einsetzten von in oder
Ergebnis als Schnittpunkt in der Form:
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
