Stochastik, Teil A, Aufgabengruppe 1
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Ein Glücksrad besteht aus fünf gleich großen Sektoren. Einer der Sektoren ist mit "0" beschriftet, einer mit "1" und einer mit "2"; die beiden anderen Sektoren sind mit "9" beschriftet.
a)
(2 BE)
Das Glücksrad wird viermal gedreht. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Zahlen , , und in der angegebenen Reihenfolge erzielt werden.
b)
(3 BE)
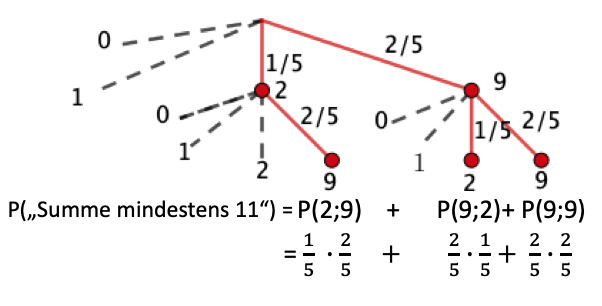
Das Glücksrad wird zweimal gedreht. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Summe der erzielten Zahlen mindestens beträgt.
- 2
Die Zufallsgröße kann ausschließlich die Werte , , und annehmen. Bekannt sind und sowie der Erwartungswert . Bestimmen Sie mithilfe des Ansatzes für den Erwartungswert die Wahrscheinlichkeiten und .
(3 BE)
- 3
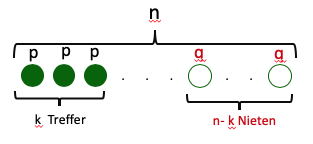
Gegeben ist eine Bernoullikette mit der Länge und der Trefferwahrscheinlichkeit . Erklären Sie, dass für alle die Beziehung gilt.
(2 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?