Gruppe A
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Zu einer vorgegebenen Strecke [EG] sollen Punkte F und H so konstruiert werden, dass sie gemeinsam mit den Punkten E und G ein Quadrat mit Diagonale [EG] bilden. Beschreiben Sie in Kurzform die dazu nötigen Konstruktionsschritte. (2 BE)
Hinweis: In der geforderten Kurzform müsste z. B. die Konstruktion einer Parallelen nicht beschrieben werden.
- 2
Jakob behauptet, dass für alle reellen Zahlen gilt. Nehmen Sie zu Jakobs Be-hauptung Stellung. Veranschaulichen Sie Ihre Stellungnahme durch ein Zahlenbeispiel. (1 BE)
- 3
Vereinfachen Sie den Term so weit wie möglich.
(2 BE)
- 4
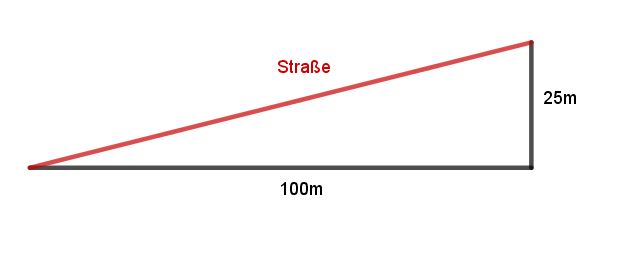
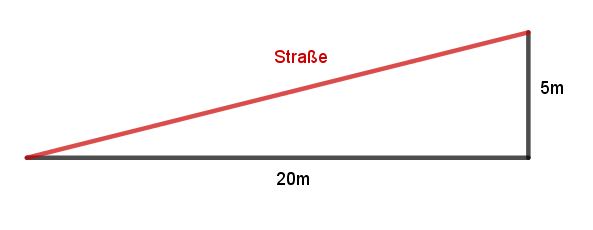
Das abgebildete Verkehrsschild gibt am Fuß einer Bergstraße deren Steigung an. Hannah sagt: „Wenn man auf dieser Straße 20 m zurücklegt, so gewinnt man dabei 5 m an Höhe.“ Ist Hannahs Behauptung richtig? Begründen Sie Ihre Antwort anhand einer geeigneten Skizze. (2 BE)
- 5
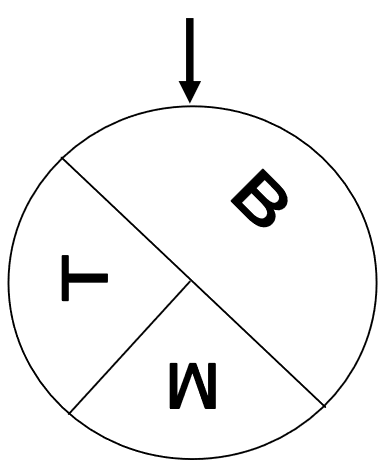
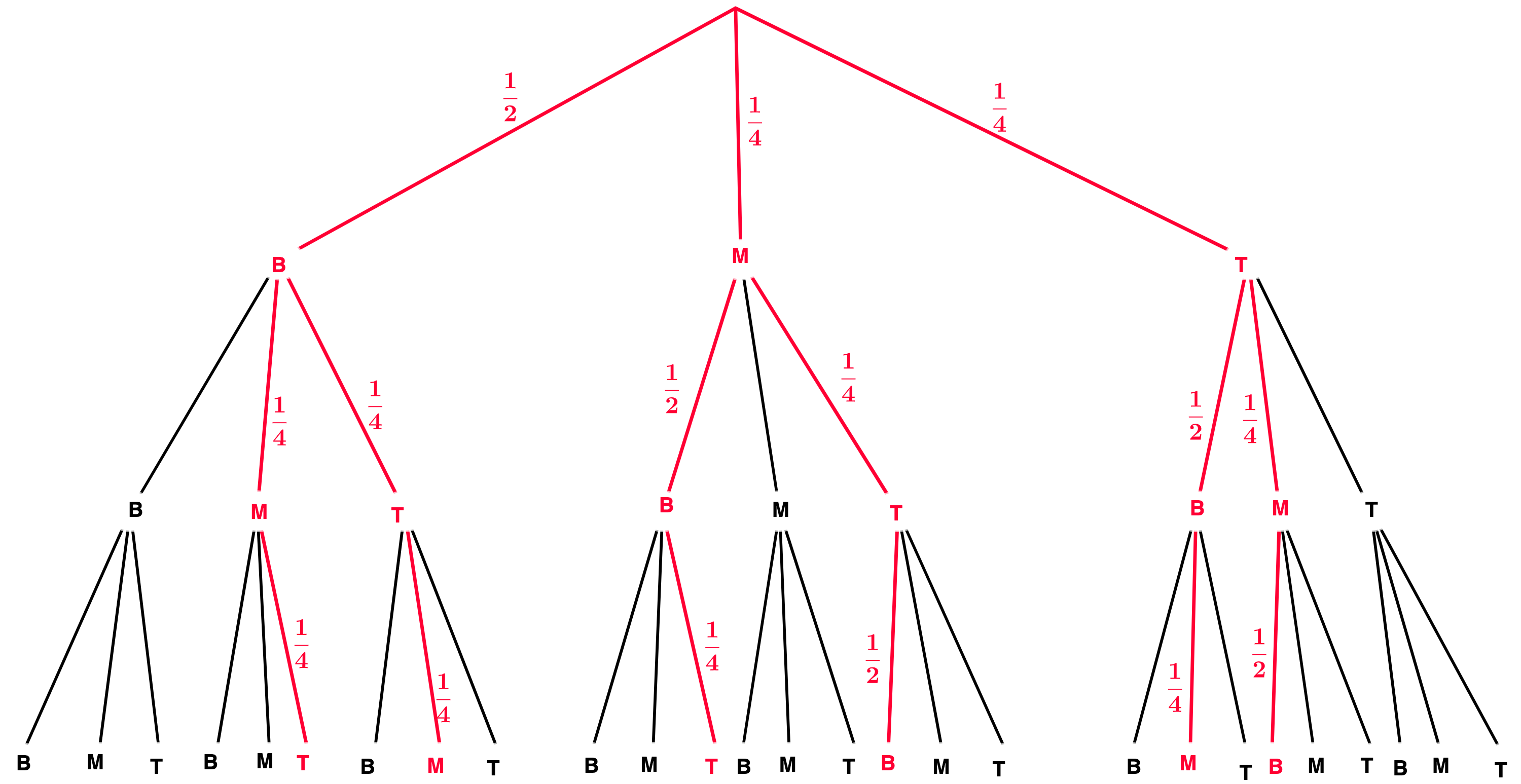
Bei dem abgebildeten Glücksrad ist der Sektor, der den Buchstaben B zeigt, doppelt so groß wie jeder der beiden anderen Sektoren. Lukas dreht das Glücksrad dreimal. Bestimmen Sie die Wahrscheinlichkeit dafür, dass er dabei jeden Buchstaben einmal erzielt. (2 BE)
- 6
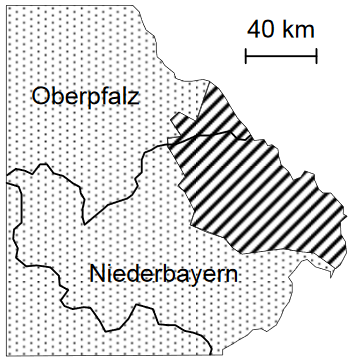
Die Trinkwassertalsperre Frauenau im Bayerischen Wald versorgt Menschen in Niederbayern und in der Oberpfalz mit Wasser. Der Stausee hat eine Oberfläche von und fasst Millionen Kubikmeter Wasser.
Berechnen Sie die durchschnittliche Tiefe des Stausees. (1 BE)
In einem Jahr wurden dem Stausee etwa 16 Millionen Kubikmeter Wasser entnommen. Damit konnte der Wasserverbrauch der 200 000 Einwohner des Versorgungsgebiets in diesem Jahr zu abgedeckt werden. Berechnen Sie, wie viel Kubikmeter Wasser in diesem Jahr pro Einwohner des Versorgungsgebiets im Durchschnitt verbraucht wurden. (2 BE)
Schätzen Sie mithilfe der abgebildeten Karte den Flächen-inhalt des schraffiert markierten Versorgungsgebiets in Quadratkilometern ab. (2 BE)
Hinweis: Bei einer Abschätzung muss grundsätzlich der Lösungsweg nachvollziehbar sein.
- 7
Eine Parabel ist gegeben durch die Gleichung .
Geben Sie die Koordinaten des Schnittpunkts der Parabel mit der y-Achse an. (1 BE)
Berechnen Sie die Koordinaten der Schnittpunkte der Parabel mit der x-Achse. (2 BE)
- 8
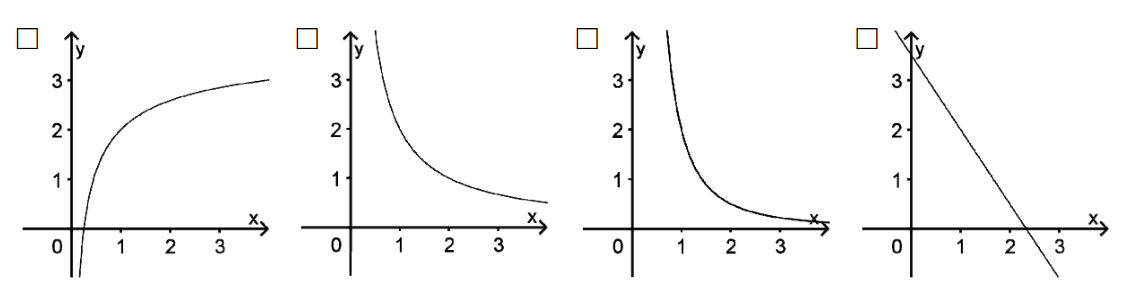
Für eine annähernd punktförmige Lichtquelle wird die Intensität y des Lichts im Abstand x von der Lichtquelle durch die Funktionsgleichung beschrieben.
Einer der abgebildeten Graphen kann zur Funktionsgleichung gehören. Kreuzen Sie an. (1 BE)
Bestimmen Sie die zu und gehörenden y-Werte. Geben Sie mithilfe Ihrer Ergebnisse an, um wie viel Prozent die Intensität des Lichts abnimmt, wenn man den Abstand zur Lichtquelle verfünffacht. (2 BE)
Lösen Sie die Gleichung nach x auf. (1 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?